Recursion Program in Java
The recursion program in Java demonstrates the usage of recursion. The process by which a function/ method calls itself, again and again, is called recursion. Each recursive call is pushed to the stack. The function/ method upon which recursion calls are made is called the recursive method. Recursion is similar to iteration. However, recursion and iteration are not the same. The similarity is both recursion and iteration execute the same piece of code again and again. In a loop, there is a condition part that is responsible for the loop termination if evaluated as false. Whereas in recursion, there is a base case responsible for the termination of recursion. Before moving ahead in recursion, we must know the following two things:
1) The base case that will terminate the recursion.
2) Must know how to divide a bigger problem into smaller problems and then, dividing the smaller problems into even smaller subproblems and continue to do so until we reach the base case.
What is the base case?
A base case is a solution to a basic problem (elementary). That is, it cannot be further divided into a smaller problem. Let’s understand recursion by the factorial of a number.
Suppose we want to find the factorial of the number 5. Now, we split this problem into further smaller problems.
5! = 5 × 4!
Now, the problem is to find the factorial of 4, and this problem can also be reduced.
4! = 4 × 3!
Similarly, 3! is reduced to
3! = 3 × 2!
For 2! we have
2! = 2 × 1!
For 1! we have
1! = 1 × 0!
In Mathematics, 0! is defined as 1. Thus,
0! = 1
Now, we cannot reduce 0! to further smaller problems as the factorial of a negative number is not possible. Thus 0! = 1 is the base case of the factorial problem. The base case helps to break the recursion. In the absence of the base case, the recursion will keep on running infinitely and eventually result in the stack overflow. The stack overflow occurs because each recursive call consumes some memory (Remember! Each recursive call is pushed to the stack), and memory is limited, resulting in the stack overflow. Let’s see some applications of recursion.
Applications of Recursion
Some common applications of recursion are:
1) To find minimum value in an Array
Filename: MinimumValueExample.java
// importing the class Arrays
import java.util.Arrays;
public class MinimumValueExample
{
// Method for finding minimum element in the array
static int findMin(int inputArr[], int index, int size)
{
// base case
if(size == 1)
{
return inputArr[index];
}
// recursively solving the problem by diving it in the smaller problems
return Math.min( inputArr[index], findMin(inputArr, index + 1, size - 1));
}
public static void main(String argvs[])
{
int numArr[] = { 27, 56, 90, 12, 120, 263 }; // input array
// displaying the input array
System.out.println("The input Array is : " + Arrays.toString(numArr));
int length = numArr.length; // finding size of the input array
int minVal = findMin(numArr, 0, length); // calling the method and storing its result
// displaying the final outcome
System.out.print("Minimum element of the input array is: " + minVal + " \n ");
}
}
Output:
The input Array is : [27, 56, 90, 12, 120, 263] Minimum element of the input array is: 12
Explanation: In the code, the method findMin() is recursively finding the minimum value element of the input array. In each recursive call, the method findMin() splits the larger array into the smaller array and keeps reducing the size of the array until the size of the input array is 1, i.e., there is only one element present in the array. If an array contains only one element, then that element is the minimum element. It forms the base case of the problem. Let’s learn how recursion work here.
In order to find the minimum value of the input array containing 6 elements, we can find the minimum value in the last 5 elements of the array and compare it with the first element. Suppose x is the minimum value of the last 5 elements, then compare x with the first element, i.e., 27. The minimum of x and 27 is our answer. The same thing is happening in the first recursive call. Mathematically,
Min of (27, 56, 90, 12, 120, 263) = Min of (27, Min of (56, 90 12, 120 263))
Similarly, for the second recursive call
Min of (27, Min of (56, 90 12, 120 263)) = Min of (27, Min of (56, Min of (90, 12, 120, 263)))
For the third recursive call
Min of (27, Min of (56, Min of (90, 12, 120, 263))) = Min of (27, Min of (56, Min of (90, Min of (12, 120, 263))))
For the fourth recursive call
Min of (27, Min of (56, Min of (90, Min of (12, 120, 263)))) = Min of (27, Min of (56, Min of (90, Min of (12, Min of (120, 263)))))
For the fifth recursive call
Min of (27, Min of (56, Min of (90, Min of (12, Min of (120, 263))))) = Min of (27, Min of (56, Min of (90, Min of (12, Min of (120, Min of (263))))))
Now we reach the base case, i.e., Min of (263), which is 263.
As each recursive call is pushed to the stack, therefore first, the last recursive call comes into the picture. It is because a stack works on the LIFO (Last In First Out) principle.
Thus, the fifth recursive call is reduced to
Min of(27, Min of(56, Min of(90, Min of(12, Min of(120, 263))))) = Min of(27, Min of(56, Min of(90, Min of(12, Min of(120, 263)))))
We know the min of 120 and 263 is 120. Thus, for the fourth recursive call, we have
Min of(27, Min of(56, Min of(90, Min of(12, 120, 263)))) = Min of(27, Min of(56, Min of(90, Min of(12, 120))))
Minimum of 12 and 120 is 12. Hence, for the third recursive call
Min of(27, Min of(56, Min of(90, 12, 120, 263))) = Min of(27, Min of(56, Min of(90, 12)))
Similarly, for the second recursive call, we have
Min of (27, Min of ( 56, 90 12, 120 263)) = Min of(27, 12)
Minimum of 27 and 12 is 12, eventually, for the first recursive call
Min of (27, 56, 90, 12, 120, 263) = 12.
Hence, 12 is the minimum value of the input array.
Note that the recursion used in the above program is called tail recursion. Because the recursive calls are the last statements in the findMin() method.
2) To print a string in reverse order
Filename: ReverseStringExample.java
public class ReverseStringExample
{
// Method for printing the input string in the reverse order
public static void reverseString(String str, int size, int index)
{
// Handling the base case
if(index == size)
{
return;
}
// recursively printing the string in the reverse order
reverseString(str, size, index + 1);
// Printing the string in reverse order
System.out.print(str.charAt(index));
}
public static void main(String argvs[])
{
String s = "apple"; // input string
int length = s.length(); // calculating length of the input string
// calling the method reverseString
reverseString(s, length, 0);
}
}
Output:
elppa
Explanation: In the above program, we have used the in-built stack that stores each recursive call to reverse the input string. The print statement coming after the recursive call is pushed to the stack. In the first recursive call, the value of the variable index is 0. Thus, the statement System.out.print(str.charAt(0)); gets pushed to the stack. The following diagram shows the same.

For the second recursive call, the value of the index is 1. Hence, the statement System.out.print(str.charAt(1)); gets pushed to stack. The current state of the stack after the second recursive call is:
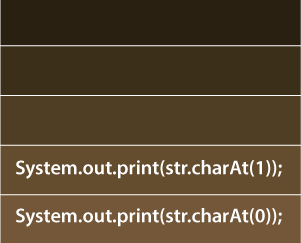
For the third recursive call, index = 2. Thus, the updated state after the third recursive call is:

Similarly, for the fourth recursive call index = 3, and the stack stores four statements. As we have shown in the following diagram.

After the fifth and final recursive call, the stack contains five statements. Observe the following diagram.

After the fifth recursive call, the value of the index is 5. Thus, we meet the base case, and the recursion is terminated. Now, whatever statement is present in the stack gets executed one by one. Since a stack works on the LIFO principle, the statement System.out.print(str.charAt(4)); gets executed first. In the string apple, the character present at the 4th index is e. Thus, the letter e is printed first. Then, the statement System.out.print(str.charAt(3)); is executed and the letter l is printed. After that, the statement System.out.print(str.charAt(2)); is executed and the letter p is printed. Then, System.out.print(str.charAt(1)); prints the letter p, and eventually the letter a is printed. Thus, it prints elppa.
The recursion used in the above program is called head recursion. In the head recursion, the recursive statement is not the last statement of the method upon which recursion is called. In the code, after the recursion, there is a print statement.
Difference between Iteration and Recursion
| Iteration | Recursion |
| Iteration is applicable to loops. | Recursion is applicable to methods. |
| Executes the code again and again until the condition part of the loop is evaluated as false. | Executes the code again and again until the base condition is met. |
| Memory consumption is less. | Memory consumption is more as each recursive call is pushed to the stack. |
| Time consumption is less. | Time consumption is more because each recursive call takes some time. |
| Iteration can continue forever if the condition part of the loop is always true. | If the base condition is not mentioned or not reached, the recursion stops due to stack overflow error. |
| Iteration is verbose. Hence, easy to understand. | Recursion is not verbose. Hence, difficult to understand. |
Which one to choose: Iteration or Recursion or both?
From the above table, one can conclude that iteration should take precedence over recursion, which is true to some extent but not always. There are many scenarios where writing code using the iterative approach becomes extremely difficult. For example, the Tower of Hanoi puzzle cannot be solved with the help of a loop.
Traversal of a tree is another example where recursion takes precedence over iteration. Thus, we observe that even though iteration is fast, knowing recursion is a must.
Recursion and iteration, when used together, are a deadly combination. There are many scenarios where it is not possible to solve the problem either using iteration or recursion. However, if recursion and iteration are both used simultaneously, we can solve the problem. One such example is to print the permutation of a string.
Permutation of a String
Suppose, we have a string abc. Then, the permutation of string abc is:
abc acb bac bca cab cba
The approach is to fix the position of one of the letters of the given string at the first position and then do the permutation of the rest of the letters of the string. The steps involved to permute the letters of the string abc is given below.
Step 1: First, we fix the letter a at the first position. Then, the permutation of the remaining letters are: bc and cb. Hence, we get abc and acb. In order to achieve the permutations of b and c. First, we fix b at the second position and c at the third position to get bc. Then, c at the second position and b at the third position to get cb.
Step 2: Now, we fix letter b at the first position. Hence, the remaining letters are a and c, and their permutation is ac and ca. This time, we get bac and bca. The permutations of the letters a and c are done in the same way we did in step 1.
Step 3: Similarly, we fix c at the first position and do the permutation of the rest of the letters to get cab and cba.
The following diagram demonstrates the same.
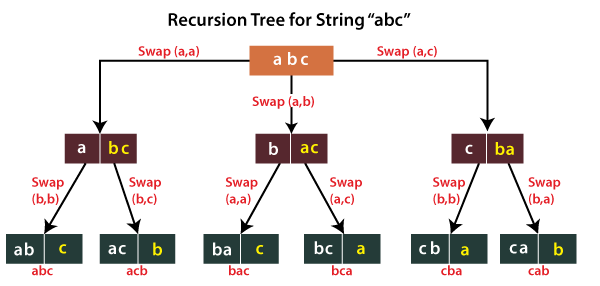
In the diagram, if we look at the first three arrows, we see Swap(a, a), Swap(a, b), Swap(a, c) written on it. Swap(a, a) means; first, we have fixed the letter a at the first position. Swap(a, b) means b is fixed at the first position, and Swap(a, c) means c is fixed at the first position. In a similar way, whatever is written on the other arrows can also be explained.
Now, observe the following Java program.
Filename: StringPermutation.java
public class StringPermutation
{
// for swapping characters of the input string
public static String swap(String s, int i, int j)
{
// convreting the string into character array
char[] ch = s.toCharArray();
// swapping characters of the index i and j
char t = ch[i];
ch[i] = ch[j];
ch[j] = t;
// converting the character array into a new String
String newString = new String(ch);
//returning the new string
return newString;
}
// Method to find the permutation of the input string.
// The method takes three arguments: first is the input string
// second is the starting index, and third is the ending index
public static void permuteString(String s, int st, int end)
{
// Handling the base case
if(st == end)
{
System.out.println(s); // printing the string
return;
}
// iterating over every character of the input string
for(int i = st; i <= end; i++)
{
// In the first swap, we are
// fixing the letters of the input string at the index st.
String swappedString = swap(s, st, i);
// recursive call for the next character
permuteString(swappedString, st + 1, end);
// second swap for doing backtracking to re-store
// the state of string that was present before the recursive call
swap(swappedString, st, i);
}
}
public static void main(String argvs[])
{
String str = "abc"; // input string
int size = str.length(); // calculating length of the input string
// calling the method permuteString()
permuteString(str, 0, size - 1);
}
}
Output:
abc acb bac bca cba cab
Explanation: In the above program, we see that the recursive call is placed between the two swap statements. The first swap is to fix the position of the letter at a particular index, and the second swap is to restore the state of the string before recursion. The above diagram also says the same. If we look at the first three arrows, we see that it is emerging from the same state of the string, i.e., abc. Each of these three arrows gives birth to two different states of the string abc. But the problem is if we have printed abc and acb, how can we print bac or bca. This is where the second swap comes to the rescue. The second swap reinstates the change, and eventually, we get the original string, i.e., abc from bca. Thus, first we moved from abc to bca and again from bca to abc, i.e., moving the reverse direction of the arrow mentioned in the diagram. This is called backtracking. After we got abc from acb, the first swap again acts on the abc and then we get bac and bca. A similar explanation for the strings cba and cab.