Practical Number in Java

In this tutorial, we will understand what is meant by practical numbers. We will understand it throughthe aid of examples and implementation in a java programming language. The practical numbers are among the top listed coding interview questions.

Any number A is known as the practical number in Java if all the numbers B that are less than A (B<A) are written as the summation of a unique proper divisor of A.

It is noted that the proper divisor of a number does not include that number itself.

Steps to acquire the Practical Numbers

Step 1: Allocateor assign a number to the variable.

Step 2: Find the proper divisors of the given number.

Step 3: Use a list to store these divisors.

Step 4: Take all the numbers that are less than the given number (range - 1 to n- 1 (n= given no.)), one by one, and try to find the subset from the list (found in step 3) whose sum is equal to the taken number.

Step 5: Check if subsets are found or not for every number from 1 to n - 1. If the subsets are found, then the given number is the practical number; otherwise, not.

Illustrations

Let us now look at some examples to understand the concept of practical numbers in a better way.

Example 1

Given, that A = 10

Then, the proper divisors of A are: 1, 2, 5

All the numbers that are less than 10 are B = {1, 2, 3, 4, 5, 6, 7, 8, 9}

Check if every number present in B or not.

1 = 1 (1 is the proper divisor of X)

2 = 2 (2 is also the proper divisor of X)

3 = 1 + 2 (1 & 2 both are proper divisors of X. Also, they are unique)

4 = 2 + 2 (2 is the proper divisor of X. However, 2 has come twice, which is not unique)

Hence, we found at least one number which does not satisfy the stated condition. Therefore, the number 10 is not a practical number.

Example 2

Given, that A = 15

Then, the proper divisors of A are: 1, 3, 5

All the numbers that are less than 15 are B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}

Check whether every number is present in B or not.

1 = 1 (1 is the proper divisor of A)

2 = 2 (2 is not the proper divisor of A)

3 = 3 (3 is also the proper divisor of A)

4 = 2+2 (neither unique nor proper divisors of A

5 = 5 (5 is also the proper divisor of A)

Hence, we found all the numbers do not satisfy the condition required for practical numbers. Thus, 15 is not a practical number.

Example 3

Given, that A = 16

Then, the proper divisors of A are: 1, 2,4, 8

All the numbers that are less than 15 are B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}

Check whether every number is present in B or not.

1 = 1 (1 is the proper divisor of A)

2 = 2 (2 is the proper divisor of A)

3 = 2+1(both are unique and the proper divisor of A)

4 = 3+1 (both are unique and the proper divisor of A)

5 = 3+2 (both are unique and the proper divisor of A)

6 = 4+2 (both are unique and the proper divisor of A)

7 = 3+4 (both are unique and the proper divisor of A)

8 = 7+1 (both are unique and the proper divisor of A)

9 = 8+1 (both are unique and the proper divisor of A)

10 = 9+1 (both are unique and the proper divisor of A)

11 = 10+1 (both are unique and the proper divisor of A)

12 = 11+1 (both are unique and the proper divisor of A)

13 = 12+1 (both are unique and the proper divisor of A)

Hence, we found all the numbers satisfy the condition required for practical numbers. Thus, 16 is a practical number.

Example 4

Given, that A = 6

Then, the proper divisors of A are: 1, 2, 3

All the numbers that are less than 15 are B = {1, 2, 3, 4, 5}

Check whether every number is present in B or not.

1 = 1 (1 is the proper divisor of A)

2 = 2 (2 is not the proper divisor of A)

3 = 3 (3 is also the proper divisor of A)

4 = 3+1 (both are unique and also the proper divisors of A)

5 = 3+2 (both are unique and also the proper divisors of A)

Hence, we found all the numbers do not satisfy the condition required for practical numbers. Thus, 6 is a practical number.

Implementation

Let us now look at a code in JAVA to understand the practical nature of the numbers starting from 1 and ending at 20.

// Online Java Compiler
// Import Statement  
import java.util.*;  


public class PracticalNumberEg
{  
// A method returns boolean value true whenever s is equal to the sum of a subset of v  
public booleanisAddSubset(int s, int size, Vector<Integer> v)  
{  
// The value of isSubset[j][i] will give out true, when  
// there is a subset of v[0..i-1] with the sum  
// equal to j   
booleanisSubset[][] = new boolean[size + 1][s + 1];  


// the answer is true whenever we get the sum as 0  
for (int j = 0; j <= size; j++)  
{  
isSubset[j][0] = true;  
}  


// the subset is not empty and the sum is 0. Hence, the  value  is false
for (int j = 1; j <= s; j++)  
{  
isSubset[0][j] = false;  
}  


// Filling the subset table in a bottom-up manner  
for (int j = 1; j <= size; j++)  
{  
for (int i = 1; i<= s; i++)  
{  
if (i<v.get(j - 1))  
{  
isSubset[j][i] = isSubset[j - 1][i];  
}  
if (i>= v.get(j - 1))  
{  
isSubset[j][i] = isSubset[j - 1][i] || isSubset[j - 1][i - v.get(j - 1)];  
}  
}  
}  
return isSubset[size][s];  
}  


// a method to keep or store all the divisors of no in the vector f  
public void keepDivisors(int no, Vector<Integer> f)  
{  
// A loop to keep track of all divisors that divides 'num'  
for (int j = 1; j <= Math.sqrt(no); j++)  
{  


// if 'j' is the divisor of 'no'  
if (no % j == 0)  
{  


// if divisor and quotient both are the same   
// then either divisor or quotient will be considered  
// for example - 9 / 3 = 3. In this case, quotient and   
// divisor both are 3. Hence, only one 3 will be stored in the vector f  
if (j == (no / j))  
f.add(j);  
else  
{  
f.add(j);  
f.add(no / j);  
}  
}  
}  
}  


// A method that returns true whenever a num is a practical number  
public booleanisPracticalNo(int num)  
{  
// a vector for storing all the factors of num
Vector<Integer> factor = new Vector<Integer>();  


// a method that fills the vector factor  
keepDivisors(num, factor);  
int size = factor.size();  


// to checking all numbers from 1 to <num
for (int j = 1; j <num; j++)  
{  
if (!isAddSubset(j, size, factor))  
return false;  
}  
return true;  
}  


// main method  
public static void main(String argvs[])  
{  
// creating an object of the class PracticalNumberExample
PracticalNumberEgpNumObj = new PracticalNumberEg();   




for(int i = 1; i<= 20; i++)  
{  
if(pNumObj.isPracticalNo(i) == true)  
System.out.println("The number " + i + " is a practical number.");  
else  
System.out.println("The number " + i + " is not a practical number.");  
}  
}  
}  

Output:

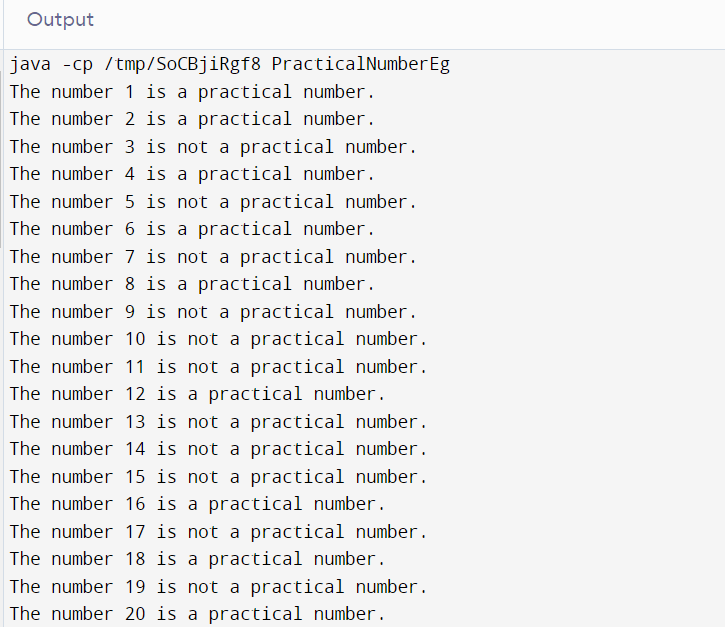
Explanation: A loop runs from 1 to 20 and it is checked whether the numbers are practical numbers or not according to the devised code. To check if the no. is a practical number or not, the function named isPracticalNo is being called. A suitable message gets printed after checking each number.

Summary

We started the tutorial by getting insights into the term practical numbers.We further understood the steps to be followed to acquire these numbers. We moved on and saw some examples to understand the concept even better and also did some analysis for the same. Finally, we took a practical approach into account. We wrote a code to observe the practical nature of the numbers ranging between 1 and 20. This is all about practical numbers.