Magic Square in Java
A square with numbers is referred to as a magic square. The numbers in a magic square of order n are arranged to ensure that the sum of all of the numbers in a row, column, and diagonal is equal to the total of all the numbers in a column and the diagonal is similar to the total of all the numbers in a row, column, and diagonal, respectively. If M is used to represent the sum, then M depends entirely on m. M does have the following qualities mathematically.
M = m(m2 + 1) / 2.
Thus,
For m = 2,
M = 2 x (2^2+ 1) / 2 = (2 x (4 + 1)) / 2 = (2 x 5) / 2 = 10 / 2 = 5
For m = 4,
M = 4 x (4^2+ 1) / 2 = (4 x (8 + 1)) / 2 = (4 x 9) / 2 = 36 / 2 = 18
For m= 9,
M = 9 x (92+ 1) / 2 = (9 x (81 + 1)) / 2 = (9 x 82) / 2 = 369
For m= 3,
M = 3 x (3^2+ 1) / 2 = (3 x (9 + 1)) / 2 = (3 x 10) / 2 = 30 / 2 = 15
Let's look at a couple of magic square illustrations.
A 15 x 15 magic square with 1695 as the value of each row, column, and diagonal exists for the value of m = 15.
104 88 72 56 40 24 8 217 201 185 169 153 137 121 120
87 71 55 39 23 7 216 200 184 168 152 136 135 119 103
70 54 38 22 6 215 199 183 167 151 150 134 118 102 86
53 37 21 5 214 198 182 166 165 149 133 117 101 85 69
36 20 4 213 197 181 180 164 148 132 116 100 84 68 52
19 3 212 196 195 179 163 147 131 115 99 83 67 51 35
2 211 210 194 178 162 146 130 114 98 82 66 50 34 18
225 209 193 177 161 145 129 113 97 81 65 49 33 17 1
208 192 176 160 144 128 112 96 80 64 48 32 16 15 224
191 175 159 143 127 111 95 79 63 47 31 30 14 223 207
174 158 142 126 110 94 78 62 46 45 29 13 222 206 190
157 141 125 109 93 77 61 60 44 28 12 221 205 189 173
140 124 108 92 76 75 59 43 27 11 220 204 188 172 156
123 107 91 90 74 58 42 26 10 219 203 187 171 155 139
106 105 89 73 57 41 25 9 218 202 186 170 154 138 122
A 13 x 13 magic square with 1105 as the value of each row, column, and diagonal exists for the value of m = 13.
77 63 49 35 21 7 162 148 134 120 106 92 91
62 48 34 20 6 161 147 133 119 105 104 90 76
47 33 19 5 160 146 132 118 117 103 89 75 61
32 18 4 159 145 131 130 116 102 88 74 60 46
17 3 158 144 143 129 115 101 87 73 59 45 31
2 157 156 142 128 114 100 86 72 58 44 30 16
169 155 141 127 113 99 85 71 57 43 29 15 1
154 140 126 112 98 84 70 56 42 28 14 13 168
139 125 111 97 83 69 55 41 27 26 12 167 153
124 110 96 82 68 54 40 39 25 11 166 152 138
109 95 81 67 53 52 38 24 10 165 151 137 123
94 80 66 65 51 37 23 9 164 150 136 122 108
79 78 64 50 36 22 8 163 149 135 121 107 93
Rules for filling the Square
Let's talk about some concepts that will be useful while designing the magic square filling rules. Every number from 1 to m2 appears on the magic square, that much is certain. The number 1 will be placed at the coordinates (m / 2, m - 1), and from that point on, each row and column will be regarded as circular and will therefore wrap around.
Rule 1: At any location, the position of the following number is determined by subtracting 1 from the row number and 1 from the column number of the previously filled number. If the computed location of the row changes to -1 at any moment, we shall wrap it around to m - 1. Similar to this, we will wrap the column around 0 if the estimated position is m.
Rule 2: If there is already a number in the magic square at the computed location, the column's computed position is reduced by two, and the row's computed position is increased by one.
Rule 3: The new position will be as follows if the computed position of the row is -1 and the computed position of the column is m: (0, m - 2).
For a better understanding, let's use an example.
276
951
438
The square matrix in the previous sentence has 9 components and is of order 3.
The first number's position is (3 / 2, 3 - 1) = (1, 2)
Number 2 is in position (1 - 1, 2 + 1), which equals (0, 3). (0, 0) [3 is rewritten to become 0]
The number three is located at (0 - 1, 0 + 1) = (-1, 1) = (3 - 1, 1) = (2, 1)
[-1 is rewritten as 3 - 1 = 2]
Number four is in the position (2 - 1, 1 + 1) = (1, 2). However, the number 1 already occupies the place of (1, 2) The result of applying rule number two is (1 + 1, 2 - 2) = (2, 0).
The place value of 5 is (2 - 1, 0 + 1) = (1, 1)
Number six is in the position (1 - 1, 1 + 1) = (0, 2)
Number 7 is located at location (0 - 1, 2 + 1) = (-1, 3) = (0, 3 - 2) = (0, 1)
[Rule 3 is used in this case]
The number 8 is located at position (0 - 1, 1 + 1) = (-1, 2) = (3 - 1, 2) = (2, 2)
[-1 is rewritten as 3 - 1 = 2]
Number 9 is in position (2 - 1, 2 + 1), which equals (1, 3). (1, 0)
[3 is rewritten to become 0]
Implementation
The code below is developed using the sample from above as a guide.
MagicSquareExample.java
public class MagicSquareExample
{
// How to create magic squares of odd sizes
public void makeSquare(int t)
{
int ms[][] = new int[t][t];
// Put 1 in its initial place.
int row = t / 2;
int column = t - 1;
// Put each value in the magic square one at a time.
for (int n = 1; n <= t * t;)
{
if (row == -1 && coloumn == t) // the 3rd prerequisite
{
coloumn = t - 2;
row = 0;
}
else
{
// if the following number is beyond the range,
// use the first rule as an assist.
if (column == t)
{
coloumn = 0;
}
// if the following number is beyond the range,
// use the first rule as an assist.
if (row < 0)
{
row = t - 1;
}
}
// the 2nd prerequisite
if (ms[row][coloumn] != 0)
{
coloumn = coloumn - 2;
row = row + 1;
continue;
}
else
{
// adjusting the value
ms[row][coloumn] = n;
n = n + 1;
}
// the first prerequisite
coloumn = coloumn + 1;
row = row - 1;
}
// the magic square as output
System.out.println(" Using the Magic Square " + t + ": \n");
System.out.println(" each column's or row's total " + t * (t * t + 1) / 2 + ": \n");
for (row = 0; row < t; row++)
{
for (coloumn = 0; coloumn < t; coloumn++)
{
System.out.print(ms[row][coloumn] + " ");
}
System.out.println();
}
}
// main method
public static void main(String[] args)
{
// When m = 11, a magic
// square of order 11 is produced.
int m = 11;
// creating an instance for the class MagicSquareExample
MagicSquareExample o = new MagicSquareExample();
// using the makeSquare method
o.makeSquare(m);
}
} Output:
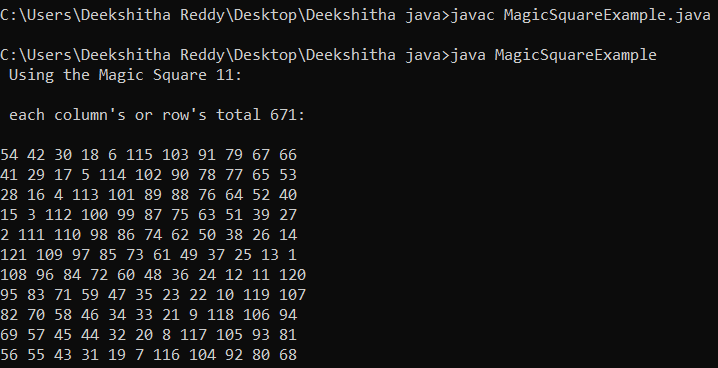
Time Complexity: The given program has an O(n2) time complexity, which denotes the number of columns or rows in the matrix form.
Space Complexity: The given program has an O(n2) space complexity, which denotes the number of columns or rows in the two - dimensional array.