Computing Digit Sum of all Numbers from 1 to n in Java
In this tutorial, we will discuss various methods to compute the sum of digits of all numbers beginning from 1 to n through a Java program. We will achieve it through examples and programs.
Example 1:
Input: num = 9
Output:
The Sum of all the digits occurring in the numbers from 1 to 9 is:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
Implementation
Approach 1: Basic
public class ComputeSum1
{
public int findSumfrom1ToN(int num1, int num2)
{
int ans = 0; // initializing the variable
// calculating the sum of digitsfor every no.
// beginning from 1 to n
for (int i = num1; i<= num2; i++)
{
ans = ans + findSumofDigits(i);
}
return ans;
}
// The method calculates the sum of
// the digits in the given number num
public int findSumofDigits(int num)
{
int sum = 0;
while (num != 0)
{
sum = sum + num % 10;
num = num / 10;
}
return sum;
}
// beginning of the main method
public static void main(String argvs[])
{
// creation of an object of the class named ComputeSum1
ComputeSum1 obj = new ComputeSum1();
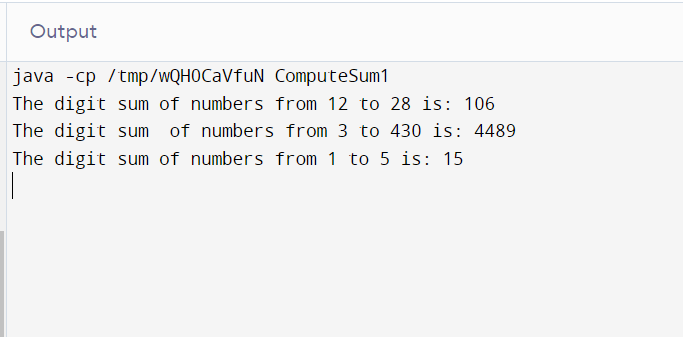
int n1 = 12;
int n2 = 28;
int ans = obj.findSumfrom1ToN(n1, n2);
// printing the result
System.out.println("The digit sum of numbers from " + n1 + " to " + n2 + " is: " + ans);
n1 = 3;
n2 = 430;
ans = obj.findSumfrom1ToN(n1, n2);
// displaying the result
System.out.println("The digit sum of numbers from " + n1 + " to " + n2 + " is: " + ans);
n1 = 1;
n2 = 5;
ans = obj.findSumfrom1ToN(n1, n2);
// displaying the result
System.out.println("The digit sum of numbers from " + n1 + " to " + n2 + " is: " + ans);
}
}
Output:
Approach 2:
This approach requires critical thinking as it is quite complicated. With good observation, one can identify the trick.
Now, let us try to observe the pattern to fund the sum of digits.
We can easilycalculate the sum from 1 to 9 by using the mathematical formula of the sum of the first n natural numbers, which is given by (n x (n + 1) / 2).
It is not required to break the task here as the range of numbers is not too large.
It is to be noted that single-digit numbers cannot be split.
Therefore,
1 + 2 + 3 + … + 9 = (9 x (9 + 1)) / 2 = (9 x 10) / 2 = 90 / 2 = 45.
This mathematical formula can be easily implemented in time complexity asO(1).
Now, let us try to get the sum of digits up to 99. To compute the sum to the number 99, It will be wise to break the task into smaller ones in the following manner.
We will break the numbers into intervals of 10.
Summation of digits of numbers in the range of 1 to 9 = 45
+
Summation of digits of numbers in the range of 10 to 19
+
Summation of digits of numbers in the range of 20 to 29
+
Summation of digits of numbers in the range of30 to 39
+
Summation of digits of numbers in the range of40 to 49
+
Summation of digits of numbers in the range of50 to 59
+
Summation of digits of numbers in the range of60 to 69
+
Summation of digits of numbers in the range of70 to 79
+
Summation of digits of numbers in the range of80 to 89
+
Summation of digits of numbers in the range of90 to 99
Now, to get the sum of digits of numbers from 10 to 19, we have to break the numbers as shown in the table below.
Table 1:
| Number | First Digit | Second Digit |
| 10 | 1 | 0 |
| 11 | 1 | 1 |
| 12 | 1 | 2 |
| 13 | 1 | 3 |
| 14 | 1 | 4 |
| 15 | 1 | 5 |
| 16 | 1 | 6 |
| 17 | 1 | 7 |
| 18 | 1 | 8 |
| 19 | 1 | 9 |
On observing the columns of the table, we find the sum of the numbers in the 1st column = 10
and the sum of the numbers present in the 2nd column is (9 x (9 + 1)) / 2 = (9 x 10) / 2 = 90 / 2 = 45
Thus, the sum of the digits of the numbers from 10 to 19 = 10 + 45, which is 55.
Again, we will calculate the sum of digits of numbers from 20 to 29. It is done similarlytothe above.
Table 2:
| Number | First Digit | Second Digit |
| 20 | 2 | 0 |
| 21 | 2 | 1 |
| 22 | 2 | 2 |
| 23 | 2 | 3 |
| 24 | 2 | 4 |
| 25 | 2 | 5 |
| 26 | 2 | 6 |
| 27 | 2 | 7 |
| 28 | 2 | 8 |
| 29 | 2 | 9 |
On observing the table, we find that the sum of the numbers present in the 1stcolumn = 20, and the sum of the numbers present in the 2ndcolumn = (9 x (9 + 1)) / 2 = (9 x 10) / 2 = 90 / 2 = 45
Thus, the sum of the digits of the numbers from 20 to 29 = 20 + 45, which is 65.
We can see that the column containing the second digit is identical in both tables. Observe the pattern.
For numbers 10 to 19, we get 10 + 45
For numbers 20 to 29, we get 20 + 45
Similarly, for 30 to 39, we will get 30 + 45. For 40 to 49, we get 40 + 45 and it will continue till the range 90 to 99
Now the overall sum of digits of numbers from 1 to 99 will be
45 + 10 + 45 + 20 + 45 + 30 + 45 + 40 + 45 + … + 90 + 45
= 45 x 10 + 10 + 20 + 30 + 40 + … + 90
= 45 x 10 + 10 x (1 + 2 + 3 + 4 + … + 9) = 45 x 10 + 10 x ((9 x (9 + 1)) / 2)
= 45 x 10 + 10 x (45)
= (sum of the first 9 natural numbers) x 10 + 45 x 10
Thus, sumOfDig(99) = sumOfDig(9) x 10 + 45 x 10
Here,sumOfDig(n) is a method that calculates the sum of digits of numbers from 1 to n. Similarly,
sumOfDig(999) = sumOfDig(99) x 10 + 45 x 100
The final formula =
| sumOfDig(10n - 1) = sumOfDig(10n - 1 - 1) x 10 + 45 x (10n - 1) |
Algorithm
We will now write an algorithm to find out the sum of digits present in numbers ranging from 1 to 445.
Based on the formula derived above, we will write an algorithm to compute the sum of digits of numbers from 1 to 445.
Step 1: Split the numbers 445 to 1 to 399 and 400 to 445.
Step 2: Compute the sum of digits of numbers from 1 to 399. From 1 to 399, we find 99 occurs 4 times: 99, 199, 299, and 399. Thus, the sum of digits of numbers from 1 to 99 will also repeat four times. Thus, the sum of digits of numbers from 1 to 399 is = 4 x sum(99) + (1 + 2 + 3) x 100.
Step 3: Calculate the sum of digits of numbers from 400 to 445. The sum is equal to 4 x 46 + summing(45).
Similarly, we can approach other numbers as well.
The sum of digits of numbers from 1 to 17 is: 81
The sum of digits of numbers from 1 to 328 is: 3241
The sum of digits of numbers from 1 to 5 is: 15
Implementation:
// JAVA program to compute the sum of digits
// in numbers from 1 to n
//importing required packages
import java.io.*;
import java.math.*;
class computeSum2{
// Function to compute the sum of digits in
// numbers from 1 to n.
static int sumOfDigitsFrom1ToN(int n)
{
// base case: if n < 10 return sum of
// first n natural numbers
//considering the example of 445
if (n < 10)
return (n * (n + 1) / 2);
// d = number of digits minus one in n
int d1 = (int)(Math.log10(n));
// computing sum of digits from 1 to 10^d1-1,
int arr[] = new int[d1 + 1];
arr[0] = 0; arr[1] = 45;
for (int i = 2; i<= d1; i++)
arr[i] = arr[i-1] * 10 + 45 *
(int)(Math.ceil(Math.pow(10, i-1)));
// calculating 10^d
int pow = (int)(Math.ceil(Math.pow(10, d1)));
// Most significant digit (msd) of n,
// For 445, msd = 4 which we can get
// using 445/100
int msd = n / pow;
return (msd * arr[d1] + (msd * (msd - 1) / 2) * pow +
msd * (1 + n % pow) + sumOfDigitsFrom1ToN(n % pow));
}
// beginning of the main function
public static void main(String args[])
{
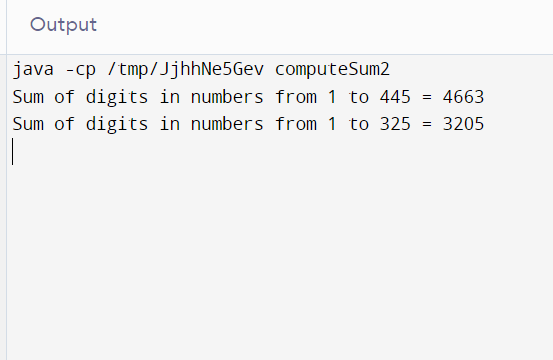
int num = 445;
System.out.println("Sum of digits in numbers " +
"from 1 to " +num + " = " +
sumOfDigitsFrom1ToN(num));
int num2 = 325;
System.out.println("Sum of digits in numbers " +
"from 1 to " +num2 + " = " +
sumOfDigitsFrom1ToN(num2));
}
}
Output:
Approach:
public class ComputeSum2
{
// Method to calculate the sum of digits in
// the numbers from 1 to n.
public int sumOfDigitsFrom1ToN(int n)
{
// dealing with the base case: if num< 10 return the sum of
// the first num natural numbers
if (n < 10)
{
return (n * (n + 1) / 2);
}
// pow = the number of digits minus 1 in the num
// For 3245, the value of pow is 2
int pow = (int)(Math.log10(n));
int a[] = new int[pow + 1];
a[0] = 0; a[1] = 45;
for (int i = 2; i<= pow; i++)
{
a[i] = a[i - 1] * 10 + 45 * (int)(Math.ceil(Math.pow(10, i - 1)));
}
// computing 10 ^ pow
int p = (int)(Math.ceil(Math.pow(10, pow)));
int msd = n / p;
return (msd * a[pow] + (msd * (msd - 1) / 2) * p +
msd * (1 + n % p) + sumOfDigitsFrom1ToN(n % p));
}
// beginning of the main method
public static void main(String argvs[])
{
// creation of an object of the class named ComputeSum1
ComputeSum2 obj = new ComputeSum2();
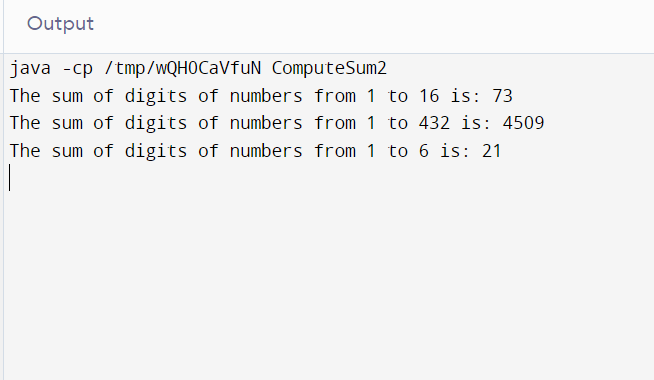
int x1 = 16;
int ans = obj.sumOfDigitsFrom1ToN(x1);
// displaying the result
System.out.println("The sum of digits of numbers from " + 1 + " to " + x1 + " is: " + ans);
x1 = 432;
ans = obj.sumOfDigitsFrom1ToN(x1);
// printing the result
System.out.println("The sum of digits of numbers from " + 1 + " to " + x1 + " is: " + ans);
x1 = 6;
ans = obj.sumOfDigitsFrom1ToN(x1);
// printing the result
System.out.println("The sum of digits of numbers from " + 1 + " to " + x1 + " is: " + ans);
}
}
Output:
Explanation: The time complexity of this program = O(pow2).
This codecan further be optimized but we will keep our discussion till here only.