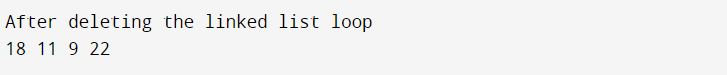Delete a Cycle from a Linked List in Java
Assume a method detectAndRemoveLoop(), which examines if a given Linked List includes a loop and, if so, eliminates this Loop and returns true. This returns false if the list does not contain a loop. The figure below depicts a linked list containing a loop. The following list must be changed using detectAndRemoveLoop() to 2->5->6->8->10->NULL.
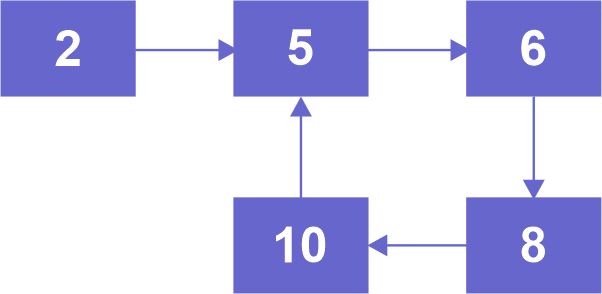
We should first identify this Loop while attempting to delete it. We only have to obtain a reference toward the Loop's final Node to delete this Loop. When we have a pointer to the final Node, we may make the next Node inside the loop NULL. For example, the diagram above shows a node with the value 5.
To obtain the reference to the final Node, we may utilize Hashing or Visited node methods. This concept is simple: that final Node is the initial Node where the next is already visited (or hashed).
The Floyd Cycle Detection technique may also detect and eliminate the Loop. Floyd's algorithm connects the slow and fast pointers at a loop node. The loop node can break the cycle. Whenever Floyd's approach is employed for loop identification, there are two ways to remove the Loop.
Method 1 (Check one by one)
Floyd's Cycle detection method is known to end anytime fast and slow pointers collide at the a cycle. One of loop nodes is indeed referred to as the common point (2 or 3 or 4, or 5 in the above diagram). Just save the address in a pointer variable, such as ptr2. Finally, beginning at the top of a Linked List, verify each node to determine if they are accessible from ptr2. Once we locate an accessible node, we know it is the beginning of the Loop in the Linked List, and we can obtain the reference to the predecessor of this Node.
Method 2
- Floyd's Cycle detection algorithm is also required through this technique.
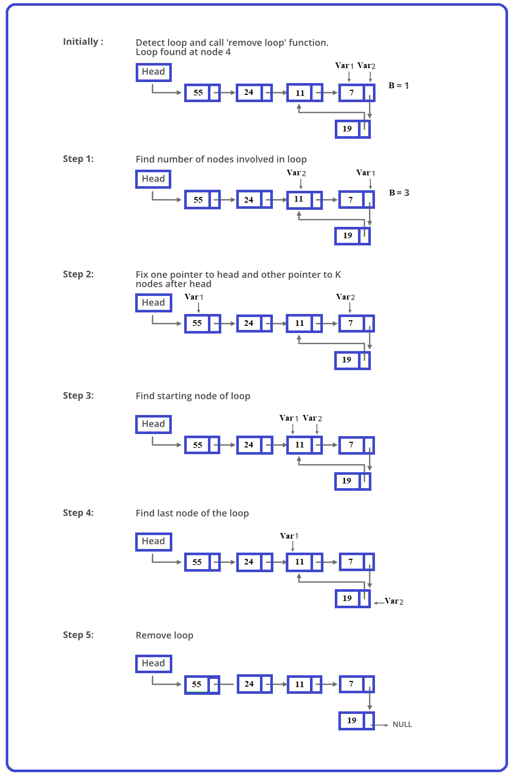
- Utilizing Floyd's Cycle detection technique, find the loop node, then obtain its reference.
- Determine how many nodes are included in the Loop. Let us say the count is B.
- Modify one pointer to the head and another to the head's Bth node.
- When you change all points simultaneously, they collide at the Loop's beginning node.
- Make a note of the Loop's last Node, subsequently change the following Node to NULL.
Filename: LinkedList.java
// A Java application for detecting and removing loops from linked list.
class LinkedList {
static Node head;
static class Node {
int data;
Node next;
Node(int A)
{
data = A;
next = null;
}
}
// List loops are recognised by a function
int RemoveTheLoopAfterDetection(Node node)
{
Node slow = node, fast = node;
while (slow != null && fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
//The Loop is formed when slow and rapid meet in the same spot.
// is available
if (slow == fast) {
removeLoop(slow, node);
return 1;
}
}
return 0;
}
//Loop removal function
void removeLoop(Node loop, Node head)
{
Node Var1 = loop;
Node Var2 = loop;
// Determine the number of nodes in the Loop.
int B = 1, i;
Node prevNode = Var1;
while (Var1.next != Var2) {
// keeping count before proceeding
prevNode = Var1;
Var1 = Var1.next;
B++;
}
prevNode.next = null;
}
// This linked list function should be displayed.
void printList(Node node)
{
while (node != null) {
System.out.print(node.data + " ");
node = Node.next;
}
}
// Driver software for testing the mentioned functions
public static void main(String[] args)
{
LinkedList Z = new LinkedList();
Z.head = new Node(55);
Z.head.next = new Node(24);
Z.head.next.next = new Node(11);
Z.head.next.next.next = new Node(7);
Z.head.next.next.next.next = new Node(19);
// Creating a testing loop
head.next.next.next.next.next = head.next.next;
Z.RemoveTheLoopAfterDetection(head);
System.out.println("After eliminating the loop from the linked list : ");
Z.printList(head);
}
}
Output:

Method 3
It is not necessary to count these nodes in Loop. Once we've identified this Loop, we may start with such a slow pointer from head and move both of the slow and fast pointers at the same rate till the fast pointers don't meet, at which point they'll meet at the beginning of the Loop.
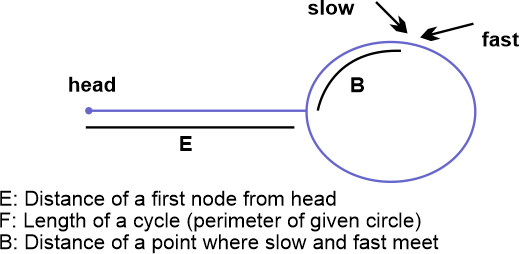
How does this function?
Make slow and fast meet following Floyd's Cycle finding technique. The figure below depicts the circumstance when the cycle is discovered.
The figure above allows us to reach the following conclusions.
Distance traveled by fast pointer = 2 * (Distance traveled by slow pointer)
(E + F*u + B) = 2*(E + F*v + B)
Take note that the fast traveled at twice its normal speed before reaching the above location.
u --> The number of full cyclic rounds completed by fast pointer before both meet for the first time.
v--> The number of full cyclic rounds completed by slow pointer before they meet for the first time.
We may get the following conclusions from the above equation:
E + B = (u-2v)*F
Which means E+B is a multiple of F.
Thus we can write E + B = i*F or m = i*F - B.
As a result, the distance traveled by the slow pointer: E, is equal to the distance moved by the fast pointer:
i*F - B or (i-1)*F + F - B (cover the loop completely i-1 times and start from F-B).
As a result, when we begin moving both pointers at the same speed, one pointer (let's call it slow) would start first from the head node of a linked list, whereas the other (let's call it fast) would start from the meeting point. Whenever the slow pointer hits the beginning of a loop (after taking E steps), the fast pointer will also take E steps because they are now going at the exact rate. They would meet at the beginning since E+B is a multiple of n and quick begins with B. Can they also meet before? No, since after E steps, the slow pointer enters the cycle for the first time.
Filename: LinkedList.java
// Java program for detecting
// as well as removing the Loop from the linked list
class LinkedList {
static Node H;
static class Node {
int data;
Node next;
Node(int A)
{
data = A;
next = null;
}
}
// Identifying list loops function
void detectAndRemoveLoop(Node node)
{
// If the list is empty or just includes one node
// without Loop
if (node == null || node.next == null)
return;
Node slow = node, fast = node;
// Take 1 and 2 steps slowly and quickly.
// ahead respectively.
slow = slow.next;
fast = fast.next.next;
// Use slow and fast pointers to look for loops.
while (fast != null && fast.next != null) {
if (slow == fast)
break;
slow = slow.next;
fast = fast.next.next;
}
/* If there is a loop */
if (slow == fast) {
slow = node;
if (slow != fast) {
while (slow.next != fast.next) {
slow = slow.next;
fast = fast.next;
}
/* since fast->next is a looping point */
fast.next = null; /* delete the loop */
}
/* If the fast and slow pointers meet in the initial location, this instance is added. */
else {
while(fast.next != slow) {
fast = fast.next;
}
fast.next = null;
}
}
}
// Print the linked list function
void printList(Node node)
{
while (node != null) {
System.out.print(node.data + " ");
node = Node.next;
}
}
// Driver code
public static void main(String[] args)
{
LinkedList Z = new LinkedList();
Z.H = new Node(55);
Z.H.next = new Node(21);
Z.H.next.next = new Node(17);
Z.H.next.next.next = new Node(7);
Z.H.next.next.next.next = new Node(19);
// Creating a testing loop
H.next.next.next.next.next = H.next.next;
Z.detectAndRemoveLoop(H);
System.out.println("After eliminating the loop from the linked list : ");
Z.printList(H);
}
}
Output:

Method 4 Hashing:
During an unsorted map, we may hash the addresses of the linked list nodes and then verify if somehow the element currently exists in the map. Whether it exists, we have arrived at an already existing node through a cycle. Therefore we must set the last Node's next reference to NULL.
Filename: LinkedList.java
// A Java application for detecting and removing loops from a linked list.
import java.util.*;
public class LinkedList {
static Node head; // head of list
/* Node of the Linked list*/
static class Node {
int A;
Node next;
Node(int d)
{
A = d;
next = null;
}
}
/* Adds a new Node to the top of the list. */
static public void push(int new_A)
{
/* 1 & 2: Insert the Data and Allocate the Node */
Node newnode = new Node(new_A);
/* 3. Make the new Node's following Node the head. */
newnode.next = head;
/* 4. Point the head to the new Node. */
head = newnode;
}
// Display the linked list function
void printList(Node n)
{
while (n != null) {
System.out.print(n.A + " ");
n = n.next;
}
}
// The method returns true if indeed the Loop is removed from linked list.
// Otherwise, the list returns false.
static boolean removeLoop(Node h)
{
HashSet<Node> s = new HashSet<Node>();
Node prev = null;
while (h != null) {
// If we already have this node
// There is a cycle in the hashmap, and we
// This Loop must be ended, therefore set the next of
// the previous pointer was set to null.
if (s.contains(h)) {
prev.next = null;
return true;
}
// When we look at the Node for
// For the very first time, put it in a hash.
else {
s.add(h);
prev = h;
h = h.next;
}
}
return false;
}
/* Driver application for testing the above function */
public static void main(String[] args)
{
LinkedList llist = new LinkedList();
llist.push(22);
llist.push(9);
llist.push(11);
llist.push(18);
/*Make a loop for testing. */
llist.head.next.next.next.next = llist.head;
if (removeLoop(head)) {
System.out.println("After deleting the linked list loop");
llist.printList(head);
}
else
System.out.println("There was no loop identified.");
}
}
Output: