Level order Traversal of a Binary Tree in Java

In Java, a level order traversal of a tree structure is also referred to as the breadth-first traversal of the binary tree.

Regarding the subsequent binary tree:

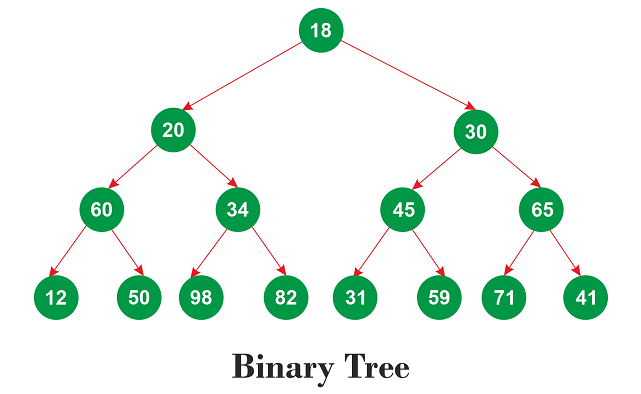
Level order traversal is as follows: 18 20 30 60 34 45 65 12 50 98 82 31 59 71 41

Using Recursion

It is possible to navigate a binary tree's level order using recursion. The recursive technique must take care of the left and right subtrees. The same is more fully demonstrated in the code below.

Implementation

Let's use the aforementioned pseudo-code to carry out the binary tree's level order traverse.

BTLevelOrder.java

// a class for producing binary tree nodes 
// A left and right reference
// as well as the node's value
// are contained in each binary tree node. 
class TreeNode   
{  
// for maintaining the node's value
int v;  
  
// to discuss the other nodes  
TreeNode l, r;  
  
// builder for the class 
// The construct TreeNode initializes the class fields.  
public TreeNode(int i)  
{  
v = i;  
r = l = null;  
}  
}  
  
public class BTLevelOrder    
{  
// the Binary Tree's top node, or root  
TreeNode r1;  
  
// function Object() { [native code] } for the BTree class  
public BTLevelOrder() { r1 = null; }  
  
// a technique for visualizing the binary tree's level order traversal 
void displayLevelOrder()  
{  
int ht1 = treeHeight(r1);  
int j;  
  
for (j = 1; j <= ht1; j++)  
{  
displayCurrentLevel(r1, j);  
}  
}  
  
// discovering the binary tree's "height"
// Keep in mind that the lengthiest path 
// from the topmost node (root node) to the leaf node, 
// which is the farthest from the root node, 
// determines the tree's height. 
int treeHeight(TreeNode r1)  
{  
if (r1 == null)  
{  
return 0;  
}  
else   
{  
// determining the left and right subtrees' heights  
int lh1 = treeHeight(r1.l);  
int rh1 = treeHeight(r1.r);  
  
// grabbing the bigger one  
if (lh1 > rh1)  
{  
return (lh1 + 1);  
}  
else  
{  
return (rh1 + 1);  
}  
}  
}  
  
// Nodes in the current level that can be printed  
void displayCurrentLevel(TreeNode r1, int l)  
{  
// Null indicates there is nothing to print.  
if (r1 == null)  
{  
return;  
}  
  
// If l == 1, 
// then there is just one node in the binary tree.  
if (l == 1)  
{  
System.out.print(r1.v + " ");  
}  
  
// We must search both the left and 
// the right sides of the current node since l > 1 denotes 
// that either node is present on the left side 
// of the current node, the right side 
// of the current node, or both sides.
else if (l > 1)   
{  
displayCurrentLevel(r1.l, l - 1);  
displayCurrentLevel(r1.r, l - 1);  
}  
}  
  
// main method  
public static void main(String args[])  
{  
// creating an instance of the class BTLevelOrder   
BTLevelOrder  t = new BTLevelOrder ();  
  
// root node  
t.r1 = new TreeNode(18);  
  
// the remaining tree nodes  
t.r1.l = new TreeNode(20);  
t.r1.r = new TreeNode(30);  
t.r1.l.l = new TreeNode(60);  
t.r1.l.r = new TreeNode(34);  
t.r1.r.l = new TreeNode(45);  
t.r1.r.r = new TreeNode(65);  
t.r1.l.l.l = new TreeNode(12);  
t.r1.l.l.r = new TreeNode(50);  
t.r1.l.r.l = new TreeNode(98);  
t.r1.l.r.r = new TreeNode(82);  
t.r1.r.l.l = new TreeNode(31);  
t.r1.r.l.r = new TreeNode(59);  
t.r1.r.r.l = new TreeNode(71);  
t.r1.r.r.r = new TreeNode(41);  
System.out.println(" Binary tree level order traversal is ");  
t.displayLevelOrder();  
}  
}  

Output:

Time Complexity:

The program's worst-case time complexity, where n is the total number of nodes in a binary tree, is O(n2). Remember that a skewed tree results in the worst-case scenario.

Space Complexity:

The program's worst-case space complexity, where n is the total number of nodes in a binary tree, is O(n). Remember that a skewed tree results in the worst-case scenario. The O(n) space call stack is used by the displayCurrentLevel() method for skewed trees. The space required in our example is O(log(n)), which is equal to the height of a balanced tree because the tree is balanced.

Using Queue

A queue can also be used to traverse a binary tree's level order. We initially use a queue to group all of a node's children. The left youngster is put in front of the right child in the queue. Because a queue functions in accordance with the FIFO (First In First Out) rule, which stipulates that the left child comes out first following by the right child, the level-ordered traverse of the tree is made possible. For a better understanding, let's look at the implementation first.

Implementation

BTLevelOrder1.java

// importing the program's necessary 
// classes for queues and linked lists 
import java.util.Queue;  
import java.util.LinkedList;  
  
  
// a class for producing binary tree nodes
// A left and right reference, as well as 
// the node's value, is contained in 
// each binary tree node. 
class TreeNode   
{  
// for maintaining the node's value  
int v;  
  
// to discuss the other nodes 
TreeNode l, r;  
  
// builder for the class 
// The construct TreeNode initializes the class fields.  
public TreeNode(int i)  
{  
v = i;  
r = l = null;  
}  
}  
  
// a class that prints a 
// level order of queue traversal
public class BTLevelOrder1   
{  
  
// the Binary Tree's top node, or root  
TreeNode r1;  
  
//  function Object() { [native code] } for the BTree class   
public BTLevelOrder1() { r1 = null; }  
  
// a technique for visualizing the binary tree's level order traversal  
void displayLevelOrder()  
{  
// making a blank queue  
Queue<TreeNode> q = new LinkedList<TreeNode>();  
  
// the node being added 
q.add(r1);  
  
while (!q.isEmpty())   
{  
// deleting the queue's front node 
TreeNode tNode = q.poll();  
  
//  the removed node's value.
System.out.print(tNode.v + " ");  
  
// Enqueue the left child if it's already there.   
if (tNode.l != null)   
{  
q.add(tNode.l);  
}  
  
// Enqueue the right child if it's already there.
if (tNode.r != null)   
{  
q.add(tNode.r);  
}  
}  
}  
  
// main method  
public static void main(String args[])  
{  
// creating an instance of the class BTLevelOrder1      
BTLevelOrder1  t = new BTLevelOrder1();  
  
// root node  
t.r1 = new TreeNode(18);  
  
// the remaining tree nodes
t.r1.l = new TreeNode(20);  
t.r1.r = new TreeNode(30);  
t.r1.l.l = new TreeNode(60);  
t.r1.l.r = new TreeNode(34);  
t.r1.r.l = new TreeNode(45);  
t.r1.r.r = new TreeNode(65);  
t.r1.l.l.l = new TreeNode(12);  
t.r1.l.l.r = new TreeNode(50);  
t.r1.l.r.l = new TreeNode(98);  
t.r1.l.r.r = new TreeNode(82);  
t.r1.r.l.l = new TreeNode(31);  
t.r1.r.l.r = new TreeNode(59);  
t.r1.r.r.l = new TreeNode(71);  
t.r1.r.r.r = new TreeNode(41);  
System.out.println(" Binary tree level order traversal is ");  
t.displayLevelOrder();  
}  
}  

Output:

Time Complexity:

The program has an O(n) time complexity, where n is the overall number of nodes in a binary tree.

Space Complexity:

The program has an O(n) space complexity, where n is the number of nodes in a binary tree.

Comparative Analysis of the Two Methods

By contrast the time and spatial complexity of the two methods, we discover that employing a queue produces the desired output significantly more quickly. The queue program's time complexity and spatial complexity are independent of the way the nodes are arranged. In other words, the program's space and time complexity are unaffected by the skewness of the tree. This is impossible with a recursive method. The placement of the tree's nodes is crucial in the recursive technique.