Maximizing Profit in Stock Buy Sell in Java
In this tutorial, we will deal with a popular problem, a favourite of interviewers. The problem is named as Maximising profit in stock Buy Sell. we will see certain approaches to solve this problem in java.
Understanding the problem statement
To understand the problem, let’s consider an integer array that shall represent the price of stocks on different dates. The stock can be purchased and sold any amount of times.
Considering an array arr1[]
int arr1[] = {40, 80, 120, 145, 10, 257, 337}
The value at the 0th position represents the cost of stock on day 1, which is 40 here.
The value at 1st position represents the cost of stock on day 2, which is 80 here.
The value at the 2nd position represents the cost of stock on day 3, which is 120 here.
The value at the 3rdposition represents the cost of stock on day 4, which is145 here.
The value at the 4thposition represents the cost of stock on day 5, which is 10 here.
The value at the 5th position represents the cost of stock on day 6, which is 257 here.
The value at the 6th position represents the cost of stock on day 7, which is 337 here.
Here, the person can buy the stock on any day and sell it on another day. Let’s say he bought it on day 1 and sold it on the 4th day. So, the profit would be 145 - 40 = 105.
Further, the person can buy a stock on day 5 and sell it on the 7th day.
So, the profit would be 337 – 10 = 327.
Thus, the net profit becomes 105 + 327 = 427.
This is the extreme profit that could be gained.
1. Simple Approach
In this approach, the stock is bought on a particular day and is sold on the same day only on the day, selling is profitable. The person has to keep a record of the maximum profit gained in the process.
The subsequent program implements the same approach.
public class MaxProfitStock
{
// A method that will return the maximum profit
// which can be earned post buying and selling of
// the stocks
public int maximumProfit(int p[], int stk, int ed1)
{
// If the stocks cannot be purchased
if (ed1 <= stk)
{
return 0;
}
// Initialization of profit variable
int pro = 0;
// Finding out the day on which the stock must
// be purchased
for (int j = stk; j < ed1; j++)
{
// Finding out the day on which the
// stock must be sold
for (int i = j + 1; i<= ed1; i++)
{
// If buying the stock on ajth day and
// selling it on anith day seems profitable
if (p[i] > p[j])
{
// Updating the current profit
// Suppose i = 9, j = 6, ed1 = 8, and stk = 1
// So, currProfit is profit found is equal to
// the profit gained when stock is sold on day 6 and purchased on day 3
// in addition to the profit gained from day 1 to day 5 in addition to the profit gained
// fromday 7 to day 8
int currProfit = p[i] - p[j] + maximumProfit(p, stk, j - 1) + maximumProfit(p, i + 1, ed1);
// Updatation of the maximum profit earned so far
pro = Math.max(pro, currProfit);
}
}
}
return pro;
}
// main method
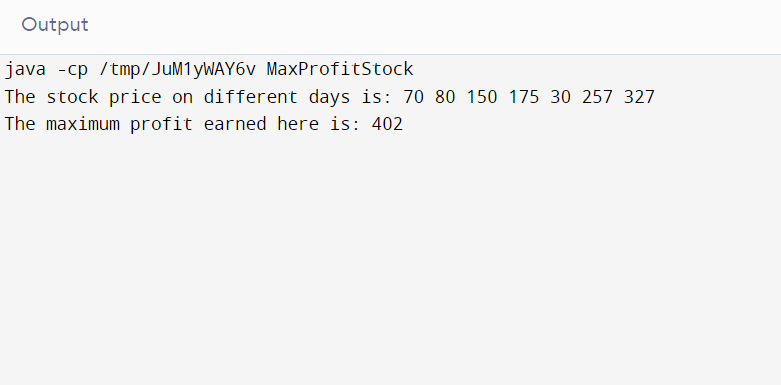
public static void main(String argvs[])
{
// assigning the price of the stock in an array
int price[] = { 70, 80, 150, 175, 30, 257, 327 };
int size = price.length; // computation of the size of array
System.out.println("The stock price on different days is: ");
for(int i = 0; i< size; i++)
{
// displaying the price of a stock
System.out.print(price[i] + " ");
}
System.out.println();
// creation of an object of the class MaxProfitStock
MaxProfitStockobj = new MaxProfitStock();
int res =obj.maximumProfit(price, 0, size - 1);
System.out.print("The maximum profit earned here is: ");
System.out.print(res);
}
}
Time complexity =O(size)
2. Well-organizedApproach
To make the solution even more resourceful, we will take into account an efficient approach where we won’t use recursion, rather we will find the local minima and local maxima The local minima will be considered as the opening index, and the local maxima will be considered as the final index. If local minima are non-existent, then return. We will have to update the solution by updating the tally of buy-sell pairs.
The following code implements this approach. Let us understand that.
// importing an important package
import java.util.ArrayList;
// to store the days when to
// buy and sell the stock
class Interval1
{
int buy1;
int sell1;
}
class MaxProfitStock1
{
// A method that calculates the maximum profit using the price of the stock
void stockBuyandSell(int p[], int size)
{
// We cannot purchase and sell the stock on that day
// Hence, there is no need to proceed further
if (size == 1)
{
System.out.println("No profit is possible since the number of days is equal to 1");
return;
}
int c = 0;
// the array containing the solution
ArrayList<Interval1> al = new ArrayList<Interval1>();
// Traversing through the given array of price
int j = 0;
while (j < size - 1)
{
// Finding the Local Minima.
//It is to be noted that the limit is (size - 2) as we are
// comparing the present element to the subsequent element.
while ((j < size - 1) && (p[j + 1] <= p[j]))
{
j = j + 1;
}
// As we reach the end, break since
// there are no possible solutions ahead
if (j == size - 1)
{
break;
}
// creating an object of the class interval
Interval1 in = new Interval1();
// Store the index of minima
in.buy1 = j + 1;
j = j + 1;
// Finding Local Maxima.
// it is to be noted that the limit is (size - 1) as we
// have to compare to previous element
while ((j < size) && (p[j] >= p[j - 1]))
{
j = j + 1;
}
// store the index for the maxima
in.sell1 = j;
al.add(in);
// Increase the number of buys or sell
c = c + 1;
}
// presenting the solution
if (c == 0)
{
System.out.println("Purchasing the stock on any provided day will hardly make any profit.");
}
else
{
int res = 0;
for (int i = 0; i< c; i++)
{
System.out.println("Purchase the stock on day: " + al.get(i).buy1
+ " "
+ "Sell the stock on day: " + al.get(i).sell1);
res = res + (p[(al.get(i).sell1 - 1)] - p[(al.get(i).buy1 - 1)]);
}
System.out.println("Hence, the total profit is: " + res);
}
return;
}
// main method
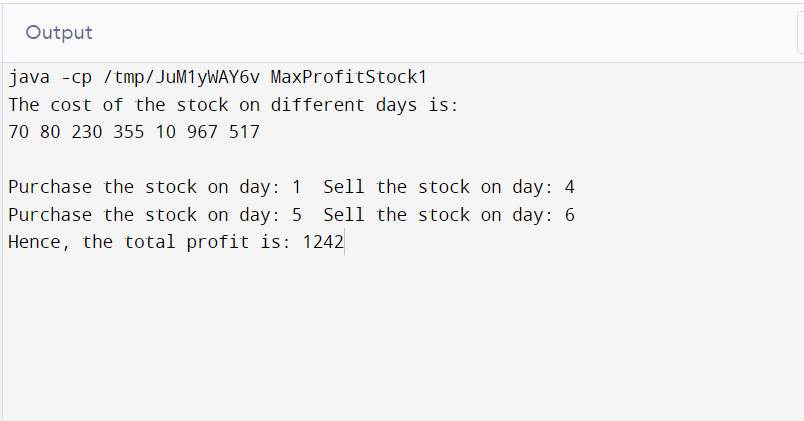
public static void main(String argvs[])
{
// creation of an object
MaxProfitStock1 obj = new MaxProfitStock1();
// price of the stock on the consecutive days
int p1] = {70, 80, 230, 355, 10, 967, 517};
int size = p1.length;// computing the size of array
System.out.println("The cost of the stock on different days is: ");
for(int i = 0; i< size; i++)
{
// displaying the price of the stock
System.out.print(p1[i]+"");
}
System.out.println("\n");
// calling the method
obj.stockBuyandSell(p1, size);
}
}
Output:
Valley Peak Approach
In this approach, we need tohave an eye on the next larger element and subtract it from the current element. We do it as the difference keeps on growing unless we reach a minimum point. It is to be noted that, no extra spaces have been used. The time complexity of this approach remains to be O(size) only.
The subsequent Java program implements this approach.
public class MaxProfitStock2
{
// A method to compute the maximum profit using the price of the stock
public int BuySellofstock(int pr[], int size)
{
// maxProfit adds up to the difference between the inline
// elements, only if they are lying in the uphill order
int maxProfit = 0;
// The loop begins from 1
// as it is doing a comparison with the previous value
for (int j = 1; j < size; j++)
{
if (pr[j] >pr[j - 1])
{
maxProfit = maxProfit + pr[j] - pr[j - 1];
}
}
return maxProfit;
}
// main method
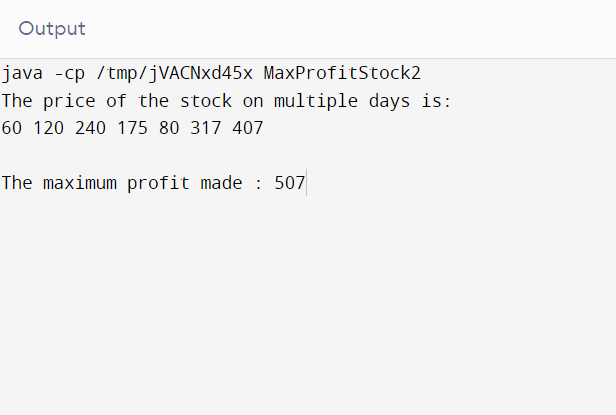
public static void main(String argvs[])
{
// creation of an object of the class MaxProfitStock2
MaxProfitStock2 obj = new MaxProfitStock2();
// cost of stock on different days
int pr[] = {60, 120, 240, 175, 80, 317, 407};
int size = pr.length; // computing the size
System.out.println("The price of the stock on multiple days is: ");
for(int i1 = 0; i1 < size; i1++)
{
// displaying the price of the stock
System.out.print(pr[i1] + " ");
}
System.out.println("\n");
// invoking the method BuySellofstock()
obj.BuySellofstock(pr, size);
int res =obj.BuySellofstock(pr, size);
System.out.print("The maximum profit made : ");
System.out.print(res);
}
}
Output:
Example:
int pr[] = { 900, 895, 655, 540, 491, 321, 241, 181, 70, 15};
The price of a stock in this case is decreasing day by day. So, if a person buys a stock on a day, then any following day after the stock is bought shall have the price of the stock less than the purchased price. Hence, one will incur a loss.