Java ArraylistRemove() Time Complexity
In this tutorial, we will learn about how we can remove time complexity in Java ArrayList. But unless we will not learn what is ArrayList, we don’t understand this process. So, first of all, we learn about what is ArrayList in java then we learn about time complexity and finally we will learn how we can remove time complexity in java ArrayList.
What is an ArrayList in Java?
The ArrayList classis part of java.util package is a dynamic array. ArrayLists can modify their size dynamically, butbuilt-in arrays are fixed in size. An ArrayList can have elements added and removed as needed, assisting the user with memory management.
In C++, ArrayLists are equivalent to vectors:
How to Create an ArrayList
The syntax for declaring an ArrayList is as follows. An ArrayList, like arrays, requires the user to declare the data type of its components, and its initial size is determined by the user.
import java.util.ArrayList; //the ArrayList class to be imported
class My_Class
{
public static void main(String args[] )
{
ArrayList<String> shapes = new ArrayList<String>();
// Make an ArrayList object with the data type of string
}
}
ArrayList Methods
The ArrayList class has a number of useful functions, which are listed below:
- Add a new item: To add an item to the beginning of an ArrayList, use the add() function. This item's index is 0 and all other indices have been incremented by1.
shapes.add("hexagon")
- To go to an item: In the ArrayList,the get() function is used to access an element using an index as input.
shapes.get(3)
- Set an item: In the ArrayListsets an element at the specified index using the set() function, which takes an index as input.
shapes.set(2, "triangle")
- Remove an item: An element in an ArrayList is removed using the remove() method, which takes an index as input. All elements in front of the eliminated element have their indexes decreased by one.
shapes.remove(1)
- Remove all items: To delete all elements from an ArrayList, use the clear() function.
shapes.clear()
- Size of ArrayList: The number of elements in an ArrayList can be found using the size() function.
shapes.size()
Implementation of ArrayList
The implementation of an ArrayList in Java code is shown below.
import java.util.ArrayList; // the ArrayList Class to be imported
class My_Class {
public static void main(String args[] ) {
ArrayList shapes = new ArrayList(); //Make an ArrayList with the new data type of string
shapes.add("pentagon");// at index 0, add pentagon
shapes.add("hexagon "); // at index 1, add hexagon
shapes.add("square"); // at index 2, add square
shapes.add("rhombus"); // at index 3, add rhombus
shapes.add("triangle "); // at index 4, add triangle
shapes.add("rectangle"); // at index 5, add rectangle
shapes.add("octagon "); // at index 6, add octagon
System.out.println(shapes); // every ArrayList shape's element to be printed.
System.out.println(shapes.get(4)); // at index 4, print element
shapes.remove(2); // at index 2, remove element
shapes.remove(5); // at index 5, remove element
System.out.println(shapes); //every element of ArrayList shapes to be printed
shapes.set(4,"circle"); // with circle at index 4, replaces element
System.out.println(shapes); // every element of ArrayList shapes to be printed
System.out.println(shapes.size()); // in the ArrayList
theelements number to be printed
shapes.clear(); // every elements in the ArrayList is remove
System.out.println(shapes); // every element of ArrayList shapes to be printed
}
}
Output:
[pentagon,hexagon, square, rhombus, triangle, rectangle, octagon]
triangle
[pentagon, square, rhombus, triangle, rectangle]
[pentagon, square, rhombus, triangle, circle]
5
[]
ArrayList:
In Java, the ArrayList is backed by an array. This aids in comprehending the implementation's internal logic. This page contains a more detailedexplanation of the ArrayList.
So, let's start with a high-level look at the temporal complexity of typical operations:
- add() takes O(1) time: although, in the worst-case situation, when a new array is built and all the elements are copied to it, it takes O(2) time (n)
- add(index, element): takes O(n) time on average.
- get(): returns a value that is always the same, the operation O(1)
- remove(): takes O(n) time to execute. To discover the element that qualifies for removal, we must loop through the entire array.
- indexOf(): also a linear time function. It iterates across the internal array, checking each entry one by one, hence this operation's temporal complexity is always O(n).
- contains(): because it's based on indexOf(), it'll take O(n) time to execute.
Time Complexity
The term "time complexity" refers to how long a block of code or an algorithm takes to process or runin relation to the size and cost of the input in programming.
It won't take an algorithm's entire execution time into consideration. Instead, it will give details on how the amounts of operations in an algorithm change the execution time (increase or decrease).
Yes, as the word implies, the time required is purely dictated by the number of iterations of one-line statements within the code.
Take a look at the code below.
#include<bits/stdc++.h>>
using namespace std;
int main()
{
cout<<” Hello Dev_1\n” ;
cout<<” Hello Dev_2\n” ;
cout<<” Hello Dev_3\n” ;
}
Despite the fact that the main() method contains three different statements, the overall time complexity is still O(1) because each statement takes a unit of time to complete.
Consider the following instance:
#include<bits/stdc++.h>>
using namespace std;
int main()
{
int j, no=35;
for(j =1 ; j<= no , j++)
{
cout<<” Hello Dev_1\n” ;
cout<<” Hello Dev_2\n” ;
cout<<” Hello Dev_3\n” ;
}
}
The O(1) piece of code (the three cout instructions) is encapsulated behind a looping statement that iterates for 'n' times. As a result, our entire time complexity is n*O(1), or O(1) (n).
You may assert that the time required is constant when an algorithm employs statements that are only executed once. However, when the statement is in a loop condition, the amount of time required increases in direct proportion to how many times the loop is set up to run.
The amount of time needed increases according to the number of times each statement is run when an algorithm contains both LOOP statements and single-executed statements, or nested LOOP statements.
Finding and recognizing the source of a recursive function's temporal complexity, for instance, can help reduce processing time from 600ms to 100ms when the function is run multiple times.That is what temporal complexity analysis is attempting to accomplish.
Notations for Time Complexity
Some of the most frequent asymptotic notations for estimating the running time complexity of an algorithm are listed below:
- O Notation
- Ω Notation
- θ Notation
- Big Oh Notation, Ο
The Big-O notation O is a systematic technique to express the upper limit of an algorithm's running time (n). It determines the worst-case time complexity or the amount of time it will take an algorithm to finish its execution.
Also, unless otherwise stated, this is the most generally used notation for describing the temporal complexity of distinct algorithms.
Definition: Allow g and f to be methods from the natural numbers set (N). If there is a constant c > 0 and a natural number n0, the function f is said to be O(g).
For any n >= n0, f (n) = cg(n). - Omega Notation, Ω
The notation is a systematic technique to express the lowest bound of an algorithm's running time (n). It determines the best-case time complexity, or how long it will take an algorithm to finish in the minimum amount of time.
Definition: There are positive constants c and n0 such that 0 cg(n) f(n) for all n n0 (g(n)) = f(n).
The following equation can be characterized as a function f(n) belonging to the set (g(n)) if and only if a positive constant c (c > 0) exists such that it is larger than c*g(n) for an adequately high value of n.
Ω(g(n)) is the minimal time required for the execution of an algorithm to be complete. - Theta Notation, θ
The notation is a systematic technique to express both the lower and upper bounds of an algorithm's running time (n).
Definition: θ(g(n)) = {f(n): there exist certain positive constants x1, x2 and n0 such that 0 ≤ x1g(n) ≤ f(n) ≤ x2g(n) for all n ≥ n0}
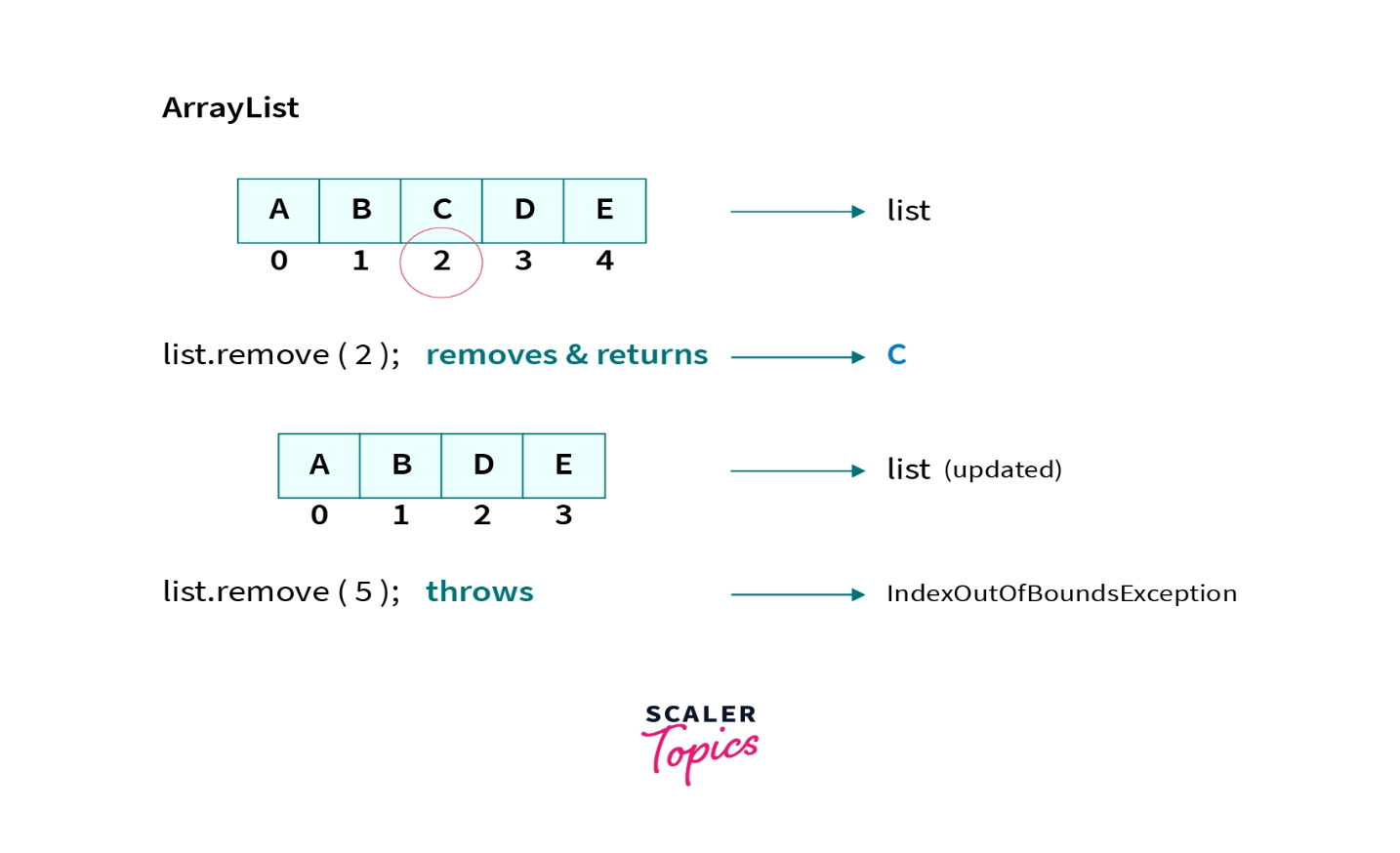
Remove Time Complexity by Index: O(N)
Because ArrayList implements the RandomAccess interface, reading anyrandom element takes only O(1) time. However, because the other parts must also be moved from one position to the left, the entire time complexity rises to O(N).
If the index is given as a parameter, the remove method will also delete and return the element that was removed. The delete method, on the other hand, throws IndexOutOfBoundsException if the index is not inside the ArrayList's range.
Remove Time Complexity by Value: O(N)
When we send an object to the remove method, it must loop through all of the list's elements until it identifies the one that needs to be removed. And, of course, the remaining pieces on the right must be shifted as well. As a result, the total temporal complexity is O(N).