Hamming Code in Java
In a computer network, hamming code is a unique set of error-correction codes. It is mostly utilised in computer graphics for mistake detection and correction during data transmission from sender to receiver. Using Hamming code, we may implement the code in Java to find and fix problems.
Because R.W. Hamming created the code to find and fix faults, it is known as Hamming code.
If the data bit count is 7, then the redundant bit count can be determined using the formula: = 24 7 + 4 + 1. As a result, there are 4 parity bits in total. To verify that the total number of 1s in the binary data is even or odd, a parity bit is a bit that is attached to the data. Error detection uses parity bits. Parity bits come in two varieties:
Even parity bit: For a specific set of bits, the number of ones is calculated in the case of even parity. If the count is odd, the parity bit value is set to 1, making the total number of 1 occurrence even. If there are an equal number of 1s in each group of bits, the parity bit has no value.
odd parity - In this scenario, the number of ones is counted for a certain group of bits. If that count is even, the parity bit value is set to 1, making the total distribution of 1s odd. If there are no more than enough odd bits in a group of bits, the parity bit has no value.
In mistake detection and repair, redundant bits and parity bits are crucial. In order to ensure that no bits were lost during the data transmission, redundant bits are extra binary bits that are added to the original data bits and are prepared to be passed from sender to receiver.
To determine if the total number of 1s is even or odd, parity bits are additional bits that are added to the original data (binary bits).
Explore the area to learn more about parity, redundancy, and Hamming code.
General Hamming Code Algorithm
For error detection and correction, we use parity bits, and the technique for doing so is called Hamming code. Following are the steps for Hamming code:
- The bit locations are initially written in binary form. The bit locations ought to be ordered from 1 to 32. (1, 10, 11, 100, etc.).
- We designate all bits that are powers of 2 as parity bits (1, 2, 4, 8, etc.).
- The remaining bit positions are all designated as data bits.
- Based on its bit position in binary representation, each data bit is a part of a distinct set of parity bits.
- The eighth parity bit covers all bit locations (8-15, 24-31, 40-47, etc.) whose binary show has 1 in the fourth position from the least bit.
- In the binary representation of the fourth parity bit, the third bit from the least bit spans all the bit locations (4-7, 12-15, 20-23, etc.).
- The second parity bit covers all bit locations (2, 3, 6, 7, etc.) whose binary show has 1 in the second position from the least significant bit.
- The second parity bit covers all bit locations (1, 3, 5, 7, 9, etc.) whose binary show has 1 in the least significant place.
- When the parity position and bit position's bitwise AND are non-zero, each parity bit covers all the bits.
- Since we check for even parity, set a parity bit to 1 if the total number of ones in the places it examines is odd.
- If all of the ones in the positions it examines are even, set the parity bit to 0.
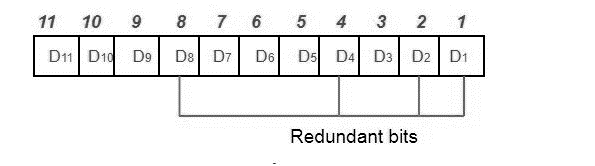
Positioning extra bits - These redundant bits are positioned at locations that are a power of two higher than the original position.
similar to the illustration given above
There are 7 bits of data.
There are 4 superfluous bits.
There are 11 bits in all.
The redundant bits are positioned at the power of 2- 1, 2, 4, and 8corresponding places.
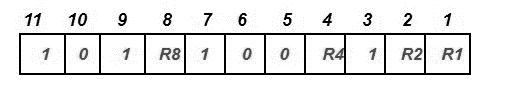
The bits will be arranged as follows, assuming the data to be conveyed is 1011001:
The parity bits are determined:
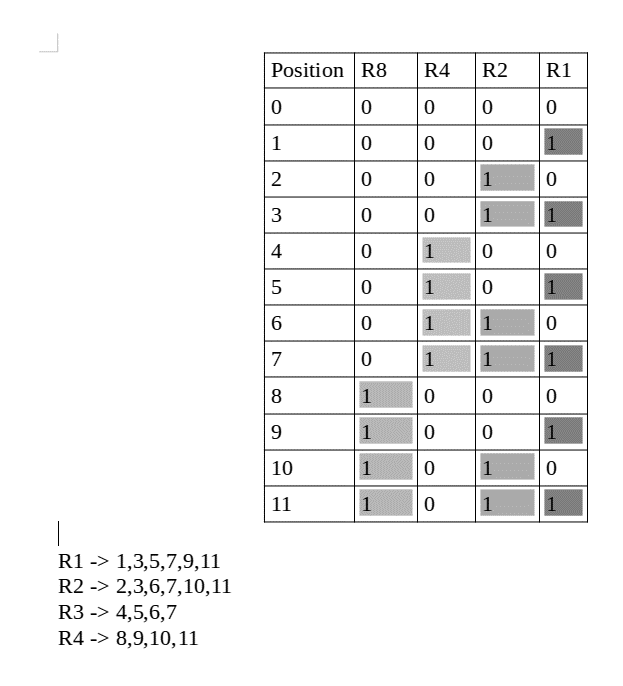
All bit positions with a 1 in the least significant position in their binary representation are used to determine the R1 bit using parity check. R1: bits 1, 3, 5, 7, 9, 11.
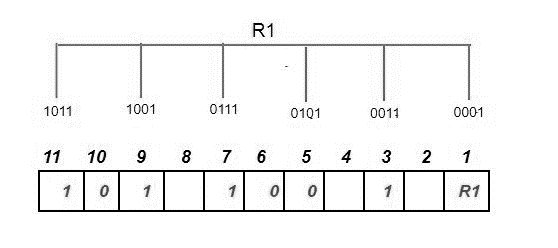
We look for even parity and then look for the superfluous bit R1. Since there are exactly as many 1s as 0s in all of the bit positions corresponding to R1, the value of R1 (the parity bit's value) is 0.
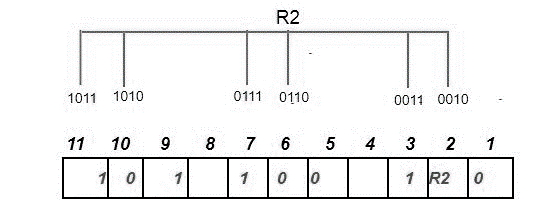
We look for equal parity and then look for the superfluous bit R2. Because there are more odd numbers than even ones in all of the bit positions corresponding to R2, the value of R2 (the parity bit's value) is 1.
With a 1 in the third position from the least bit, a parity check at each location in a binary show identifies the R4 bit. R4: bits 4, 5, 6, 7
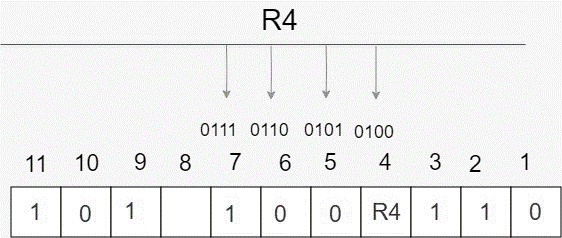
We look for even parity and then look for the redundant bit R4. Since there are more odd numbers than even ones in all of the bit places corresponding to R4, R4's parity bit value equals 1.
Using a parity check at each bit location for a binary representation with a 1 in the fourth position from the least significant bit, the R8 bit is identified. R8: bit 8,9,10,11
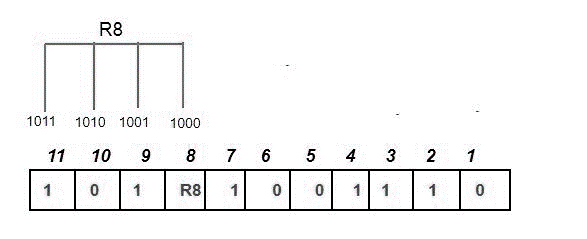
We look for even parity and then look for the redundant bit R8. Since there are exactly as many 1s as 0s in R8's corresponding bit places, R8's parity bit value is 0. Thus, the information conveyed is:

Error detection and correction: Assume that during data transmission, the 6th bit in the example above was altered from 0 to 1, which would result in new parity values for the binary number:
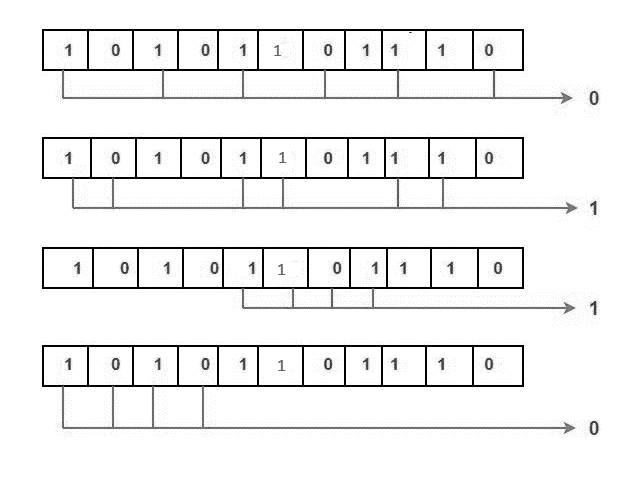
The binary number 0110 is generated by the bits, and its decimal representation is 6. Bit 6 therefore contains a mistake. The 6th bit is altered from 1 to 0 to fix the issue.
//
Package Example;
import java.util.*;
// to implement the Hamming Code feature in Java, develop an HC class.
class HC {
// main() method start
public static void main(String args[])
{
// declare variables and array
int s, HCS, errorposition;
int a[];
int hammingCode[];
// create an instance of the scanner class to hold user input.
Scanner sn = new Scanner(System.in);
System.out.println("Enter the data's bit size.");
s = sn.nextInt();
// initialize array
a = new int[s];
//get the user to provide the info we wish to send
for(int j = 0 ; j < s ; j++) {
System.out.println("Enter " + (s - j) + "-bit of the data:");
// data entered by the user to populate an array
a[s - j - 1] = sc.nextInt();
}
// print the user entered data
System.out.println("The data which you enter is:");
for(int k = 0 ; k < s ; k++) {
System.out.print(arr[s - k - 1]);
}
System.out.println(); // for next line
// Using the getHammingCode() method and adding the result to the hammingCode array.
HCode = getHCode(a);
HCS = HCode.length;
System.out.println("Your data's produced hamming code is:");
for(int i = 0 ; i<HCS; i++) {
System.out.print(hammingCode[(HCS - i - 1)]);
}
System.out.println(); // for next line
// The difference between the original data and the returned hammingCode is represented by the extra parity bits.
System.out.println("Enter the position of a bit to change the original data in order to discover errors at the receiver end."
+ "(0 for no error):");
errorPosition = sn.nextInt();
// close Scanner class object
sn.close();
// Verify if the user-entered location is zero (0).
if(errorPosition != 0) {
// change a user-entered position's bit
HCode[errorPosition - 1] = (HCode[errorPosition - 1] + 1) % 2;
}
// print sent data to the receiver
System.out.println("Sent Data is:");
for(int k = 0; k <HCS; k++) {
System.out.print(hammingCode[HCS - k - 1]);
}
System.out.println(); // for next line
receiveData(HCode, HCS - a.length);
}
// construct a method called getHammingCode() that returns the hamming code for the data we wish to deliver.
static int[] getHCode(int data[]) {
// define an array that will contain the data's hamming code.
// RD = return Data
int RD[];
int s;
// code to get the required number of parity bits
int i = 0, parityBits = 0 ,j = 0, k = 0;
s = data.length;
while(i< s) {
// The current location (number of bits traversed + number of parity bits + 1) must equal 2 powers of parity bits.
if(Math.pow(2, parityBits) == (i + parityBits + 1)) {
parityBits++;
}
else {
i++;
}
}
//The RD's size is equal to the combined size of the original data and the parity bits.
RD = new int[s + parityBits];
// We initialise the RD array with '2' to represent an unset value in the parity bit location.
for(i = 1; i<= RD.length; i++) {
// condition to find parity bit location
if(Math.pow(2, j) == i) {
RD[(i - 1)] = 2;
j++;
}
else {
RD[(k + j)] = data[k++];
}
}
// Set even parity bits at parity bit locations using a for loop.
// PB = parity bit
for(i = 0; i<PB; i++) {
RD[((int) Math.pow(2, i)) - 1] = getPB(RD, i);
}
return RD;
}
// develop a method called getPB() that returns parity bits dependent on power
static int getPB(int RD[], int pow) {
int PB = 0;
int s = RD.length;
for(int i = 0; i< s; i++) {
// Verify whether or not RD[i] contains an unset value.
if(RD[i] != 2) {
// If not, we increase the value of the index in k by 1 to save it.
int k = (i + 1);
// binary conversion of the value of k
String sr = Integer.toBinaryString(k);
//We now check the value there to see if the binary value of index has a bit set to 1 at the 2(power) location. Depending on whether the value is 1 or 0, we will decide the parity value.
int temp = ((Integer.parseInt(sr)) / ((int) Math.pow(10, p))) % 10;
if(temp == 1) {
if(RD[i] == 1) {
PB = (PB + 1) % 2;
}
}
}
}
return PB;
}
// To find errors in the received data, create the receiveData() method.
static void receiveData(int data[], int PBs) {
// declare variable pow, which we use to get the correct bits to check for parity.
int p;
int s = data.length;
//establish parity array to store the parity check value
int parityArray[] = new int[PBs];
// For recording the integer value of the error location, we utilise the errorLocation string.
String errorLocation = new String();
// To check the parities, use a for loop.
for(p = 0; p <PBs; p++) {
// to extract the bit from 2, use a for loop (power)
for(int i = 0; i< s; i++) {
int j = i + 1;
// binary conversion of the value of j
String sr = Integer.toBinaryString(j);
// find bit by using sr
int bit = ((Integer.parseInt(sr)) / ((int) Math.pow(10, pow))) % 10;
if(bit == 1) {
if(data[i] == 1) {
parityArray[p] = (parityArray[p] + 1) % 2;
}
}
}
errorLocation = parityArray[p] + errorLocation;
}
// This provides the values for the parity check equation. We will now use these numbers to determine if there is a single bit issue and subsequently fix it.
// To determine if a single bit mistake exists or not, we use the parity check equivalent values provided by errorLocatiion. If it's there, we fix it.
int finalLocation = Integer.parseInt(errorLocation, 2);
// check whether the finalLocationa value is 0 or not
if(finalLocation != 0) {
System.out.println("Error is found at location " + finalLocation + ".");
data[finalLocation - 1] = (data[finalLocation - 1] + 1) % 2;
System.out.println("the problem is fixed and the code is:");
for(int i = 0; i< s; i++) {
System.out.print(data[s - i - 1]);
}
System.out.println();
}
else {
System.out.println("The data that was received is flawless.");
}
// print the original data
System.out.println("The data sent from the sender:");
p = PBs - 1;
for(int k = s; k > 0; k--) {
if(Math.pow(2, p) != k) {
System.out.print(data[k - 1]);
}
else {
// decrement value of pow
p--;
}
}
System.out.println(); // for next line
}
}
Output:
Enter the data's bit size
7
Enter 7-bit of the data:
1
Enter 6-bit of the data:
1
Enter 5-bit of the data:
0
Enter 4-bit of the data:
1
Enter 3-bit of the data:
0
Enter 2-bit of the data:
0
Enter 1-bit of the data:
1
The data which was given is:
11001001
The hamming code generated for given data:
11001001101
For detecting error at the receiver end, enter position of a bit to alter original:
3
Sent data is:
11001001001
Error is found at position 3.
After correcting the error, the code is:
11001001101
The data sent from the sender:
1101001