Sierpinski Number in Java

The Sierpinski triangle—is it a fractal?

The Sierpinski Triangle fractals. A self-similar fractal is the Sierpinski triangle. It is made of an equilateral triangle with its residual area successively reduced by smaller equilateral triangles.

Here, it contains the covering set, which is 3, 5, 7, 13, 19, 37, 73, it is a Sierpinski number. It is known as a covering set because each number of the structure 78557*2n+1 is distinguishable by one of these little primes.

Java Sierpinski Number

To determine whether a given number is a Sierpinski number, use Java programmes and Sierpinski numbers. Since the Sierpinski number is directly related to the Sierpinski triangle, we will first study about it before continuing with this part.

The triangle of Sierpinski

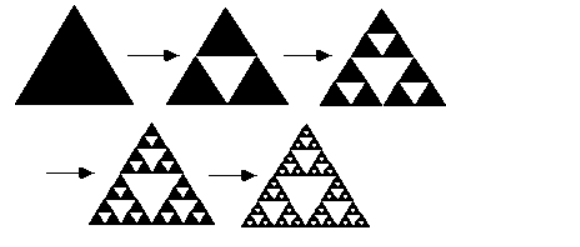
A self-similar geometric shape, the Sierpinski triangle, also known as the gasket triangle. It signifies that the thing maintains the same appearance or structure even when we zoom in on it. An illustration of a fractal is the Sierpinski triangle, which is produced by sketching a triangle and then erasing an internal triangle made by joining the midpoints of the outer triangle's sides (a curve or geometric figure, each part of which has the same statistical character as the whole). This procedure is repeated indefinitely and recursively.

The following graphic illustrates the four-times-iterated Sierpinski triangle. The phrase "a fractal and attractive fixed set with the general shape of an equilateral triangle, subdivides a triangle into smaller triangles, recursively" can also be used to describe it.

N=3k-1 is the Sierpinski triangle counting formula.

The user can carry on with (or repeat) this procedure. We remove the "centre" of each remaining triangle, leaving behind three smaller triangles, each half the size of the parent triangle (and one-fourth of the original triangle). There are nine triangles left at this point. Twenty-seven small triangles are left at the following iteration, 81 at the following, and 3 N small triangles at the next step. It is simple to verify that the size of the triangles left after the Nth iteration is exactly 1/2N of the initial size.

Sierpinski Number

An integer k*2n+1 that is all-composite for all-natural numbers n is known as a Sierpinski number. In other words, if all the individuals in the following settings are composite, then k will be a Sierpinski number.

The sequence is A076336 from the OEIS. The smallest Sierpinski number is the first in the series, 78557; however, this is only an assumption (not yet proved). Because it contains the covering set of 3, 5, 7, 13, 19, 37, and 73, it is a Sierpinski number. The type 78557*2n+1 is regarded as a covering set because every number in it can be divided by one of these little primes.

Few Sierpinski Number examples:

1290677, 1624097, 1259779, 1518781, 1777613, 2131043, 2131099, 2191531, 2510177, 2541601, 2576089, 2931767, 3083723, 3098059, 3555593, 3608251, 271129, 271577, 322523, 271129, 271577, 322523, 327739, 482719, 575041

The Java programmed Sierpinski Triangle

// Java printing program statement
// The Sierpinski triangle.
import java.util.*;
import java.io.*;


class Sierpinski
{
static void printSierpinski(int n)
{
for (int y = n - 1; y >= 0; y--) {


// printing area until
// the value of y
for (int i = 0; i < y; i++) {
System.out.print(" ");
}


// printing '*'
for (int x = 0; x + y < n; x++) {


// printing "*" when necessary
// role is fulfilled by the and
// wherever value, x and y's values
// is 0, "*" has been printed.
if ((x & y) != 0)
System.out.print(" "
+ " ");
Else
System.out.print("* ");
}
System.out.print("\n");
}
}
// Driver code
public static void main(String args[])
{
int n = 16;
// Function invocation
printSierpinski(n);
}
} 

Output:

What is the purpose of Sierpinski's Triangle?

The Sierpinski triangle exercise exemplifies the basic ideas of fractals. It shows how a pattern may repeat itself repeatedly at various scales and how this complex shape can be created using straightforward repetition. Each student creates a fractal design triangle out of successively smaller triangles.

In Sierpinski, how many triangles are there?

We are left with three triangles, each of which is precisely one-fourth the size of the original triangle and has dimensions that are exactly one-half its original size. Each of the surviving triangles also resembles the original.