Centered Square Numbers in Java

In this tutorial, we will understand how to check the number is a centered square number. It is one of the prevalent interview questions of IT companies. Firstly, we will understand the meaning of centered square numbers later we will create a java program for the same.

Centered Square Numbers

Centered Square numbers are the figurate numbers

that are recursively described as:

Q(num) = Q(num - 1) + 4 x (num - 1), where num >= 1 and Q(0) = 1  

Example:

For num = 1ry of Java

Q(1) = Q(1 - 1) + 4 x (1 - 1) => Q(1) = Q(0) + 4 x 0 = 1 + 0 = 1

For num = 2

Q(2) = Q(2 - 1) + 4 x (2 - 1) => Q(2) = Q(1) + 4 x 1 = 1 + 4 = 5

For num = 3

Q(3) = Q(3 - 1) + 4 x (3 - 1) => Q(3) = Q(2) + 4 x 2 = 5 + 8 = 13

For num = 4

Q(4) = Q(4 - 1) + 4 x (4 - 1) => Q(4) = Q(3) + 4 x 3 = 13 + 12 = 25

For num = 5

Q(5) = Q(5 - 1) + 4 x (5 - 1) => Q(5) = Q(4) + 4 x 4 = 25 + 16 = 41

Implementation

Approach 1: Recursive

Let us now see a recursive java program to find the first fifteen centered square numbers.

public class CenteredSquareNumber   
{  
public int detectCenteredSqureNum(int n)   
{  
// dealing with the base case  
if(n == 1)  
{  
    return n;  
}  
// calculation of the central square number recursively   
return detectCenteredSqureNum(n - 1) + 4 * (n - 1);  
}  
// beginning of the Main method  
public static void main(String[] argvs)   
{  
// creation of an object of the class named CenteredSquareNumber  
CenteredSquareNumber obj = new CenteredSquareNumber();  
// calculation of 15 centered square numbers  from the beginning
int num = 15;  
System.out.println("The first " + num + " Centered Square Number are: \n");  
for(int j = 1; j <= 15; j++)  
{  
int res = obj.detectCenteredSqureNum(j);  
System.out.print(res + " ");  
}  
}  
}  

Output:

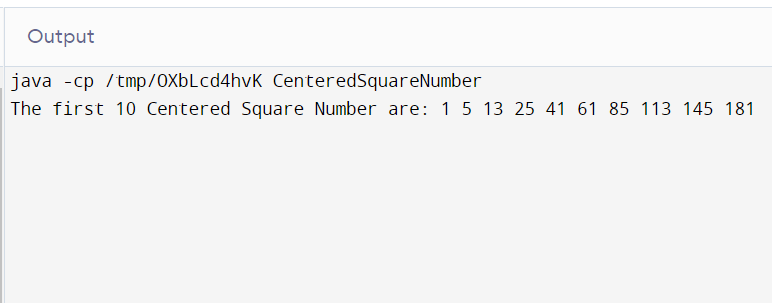
Explanation: The above program has space complexity = O(1).

The time complexity of the program O(t), where t is the t^th position of the central square number that is to be found.

Approach 2: Iterative

The above program is optimized to reduce the complexities. Here, an array is used to store the result.

public class CenteredSquareNumber2   
{  
// Main method  
public static void main(String[] argvs)   
{  
// calculating the initial 15 centered square numbers  
int n = 15;  
// creation of an array to store the calculated centered square number  
int res[] = new int[n + 1];  
System.out.println("The first " + n + " Centered Square Number are: \n");  
for(int j = 1; j <= 15; j++)  
{  
// dealing with the base case  
if(j == 1)  
{  
    res[j] = 1;  
}  
else  
{  
    res[j] = res[j - 1] + 4 * (j - 1);  
}  
// displaying the result  
System.out.print(res[j] + " ");  
}  
}  
}  

Output:

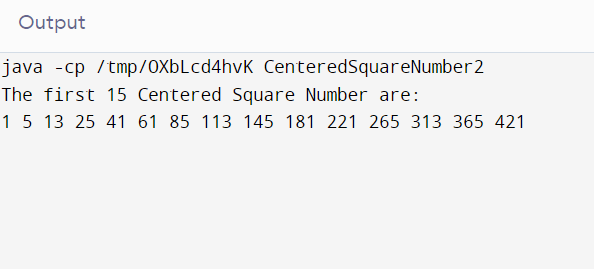
Explanation: The space complexity of the above program =  O(n). here, n is the total number of central squared numbers to be calculated. and the time complexity = O(1).

Approach 3:

This is another optimized approach.

public class CenteredSquareNumber3  
{  
// beginning of the main method
public static void main(String[] argvs)   
{  
// calculating the first 15 centered square numbers  
int n = 15;  
// A variable to store just the last computed centered square number  
int lastCenSqrdNum = 0;  
System.out.println("The first " + n + " Centered Square Number are: \n");  
for(int j = 1; j <= 15; j++)  
{  
// dealing with the base case  
if(j == 1)  
{  
    lastCenSqrdNum = 1;  
}  
else  
{  
    lastCenSqrdNum = lastCenSqrdNum + 4 * (j - 1);  
}  
// displaying the result  
System.out.print(lastCenSqrdNum + " ");  
}  
}  
}  

Output:

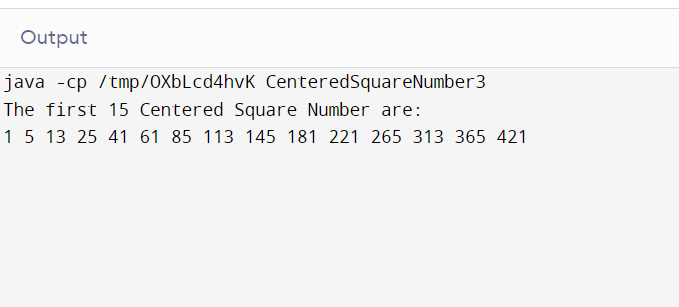
Explanation: The time complexity here = O(1). The space complexity also is O(1) as no arrays have been taken into account to store the resultant.

Approach 4: Mathematical formula

Q(num) = num² + (num - 1)², where num>= 1

Example:

For num = 1

Q(1) = 1² + (1 - 1)² => Q(1) = 1 + 0² = 1 + 0 = 1

For num = 2

Q(2) = 2² + (2 - 1)² => Q(2) = 4 + 1² = 4 + 1 = 5

public class CenteredSquareNumber4  
{  
// Beginning of the Main method  
public static void main(String[] argvs)   
{  
// calculating the first 15 centered square numbers  
int n = 15;  
System.out.println("The first " + n + " Centered Square Number are: \n");  
for(int j = 1; j <= 15; j++)  
{  
int res = (j * j) + ((j - 1) * (j - 1));  
// displaying the result  
System.out.print(res + " ");  
}  
}  
}  

Output:

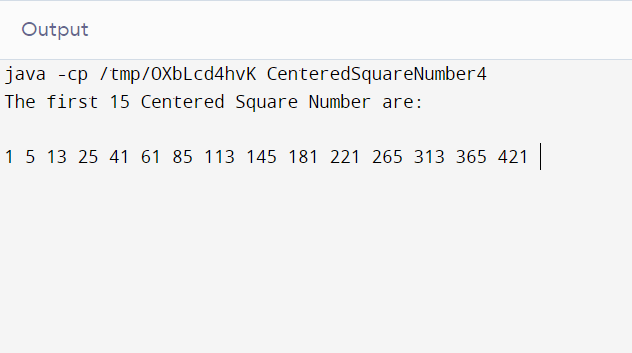
Explanation: The time complexity = O(1) .The space complexity = O(1).