Bellman Ford Algorithm in Java

Numerous algorithms have been used in dynamic programming to determine the shortest path inside a graph. Among them are Floyd, all-pair shortest path problem, Breadth First Search, Depth First Search, Dijkstra's technique, and the bidirectional approach. Dijkstra's algorithm is the one that's most frequently employed. One limitation of the approach is that it cannot be used for graphs with negative edge weights. Another distinction is that although Bellman-Ford iterates through each edge, the Dijkstra method only considers a vertex's immediate neighbors.

The solution to this problem may be found using the Bellman-Ford algorithm. The two low-edge weights are the subject of everything. This section will explain the Bellman-Ford algorithm using examples and demonstrate how to use it in a Java program.

The Bellman-Ford Algorithm

It is similar to Dijkstra's algorithm and uses a single-source shortest path (lowest weight) approach. When we need to determine the shortest route in a graph, we may utilize it. It solves the with negative edge weights, as you might have seen. A cycle's ability to create a negative result when its edges are added together is a limitation of the algorithm. Take into consideration the cycled graph below.

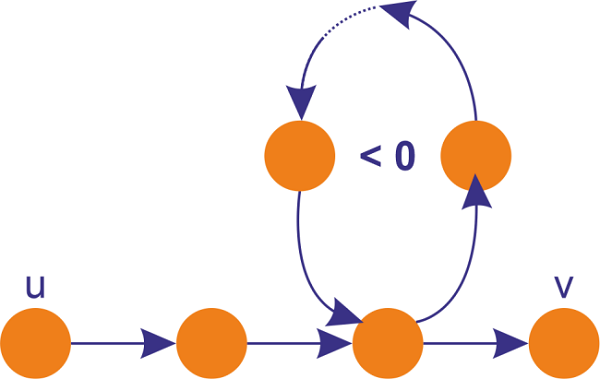
The algorithm's storage and time complexity are both (v*e) (v). The procedure should be used if the graph's edge weights are negative. The Bellman-Ford algorithm is thus applicable in the following circumstances:

• Negatively weighted edges
• Indirect Cycles with Positive Edge Weights > 1

In the case of all negative arcs, the technique is very slower than Dijkstra's algorithm.

Steps for finding the Shortest path

The Bellman-Ford algorithm's steps for determining the shortest path from the source to each vertex are as follows:

• In this stage, the source's distance to every vertex is set to infinity, while the source's distance is set to 0. Make an array dist[] of size |V| except dist[src], the source vertex having all values set to infinity.
• The smallest distances are computed in this stage. Execute the steps below |V|-1 times, where |V| seems to be the number of a vertex in the graphs g. For every edge u-v, repeat these procedures. Follow these steps for each edge u-v. Increase dist[v] to dist[v] = dist[u] + weight of edge UV if dist[v] > dist[u] + weight of the edge UV.
• When there is a negative weight cycle inside the graph, the next step reports it. Once more, travel along each edge and perform steps u-v for each edge. Graph demonstrates negative weighted cycle if dist[v] > dist[u] + edge weight uvUV.
• The idea underlying step 3 is that if the graph doesn't have a negative weight of the cycle, step 2 assures the very lowest lengths. There is a negative value cycle if we iterate throughout all edges one further time and obtain the shortest route for every vertex.

How The Bellman-Ford Algorithm Works

The Bellman-Ford algorithm functions similarly to Dijkstra's algorithm. Like Dijkstra's algorithm, it repeatedly cycles over all edges and changes the lengths at the initial node. The key difference is that the prioritized queue does not get used. Sometimes shortest paths might not exist if a graph G=(V, E) has a negative weight cycle. The Bellman-Ford algorithm identifies a negative weight cycle or all shortest paths from the source of length s to all destinations of length v.

The technique gives a boolean value of TRUE when and only if the weighted directed graph G(V, E) does not contain any negative-weight cycles that can reach first from the source. The algorithm generates the weights as well as the shortest path. The method suggests there is no answer when such a cycle exists. There is an answer when such a cycle exists.

Algorithm

INITIALIZE-SOURCE (G, s)  
for i <- 1 to |V[G]|-1  
do for each edge (U, V) ϵ E[G]  
do RELAX (U, V, W)  
for each edge (U, V) ϵ E[G]  
do if distance[V] > distance[U] + w(U, V)  
then return FALSE  
return TRUE  

Pseudo code for Bellman Ford Algorithm

BellamanFord (G, V, E, S)  
Step1:  
for each vertex v ϵ G do  
distance[v] = ∞  
distance[source] =  0
  
Step 2:  
Relax (u, v, w)  
for i = 1 to |v|-1  
           for each edge (u, v) ϵ G do  
           (distance[v] > distance[u]+w(u, v))  
           (distance[v] <- distance[u]+w(u, v))  
Step 3:  
for each edge (u, v) ϵ G  
if (distance[u]+w(u, v)< distance[v])  
return "Graph G contains the negative cycle.”  
return distance  

Java Program for the implementation of the Bellman Ford algorithm

BellmanFord.java

import java.util.ArrayList;  
import java.util.List;  
//class Graphs are created
class Graphs   
{  
//the vertices of the graph G  
private int Vertex;    
//edges in the graph  
private List<Edge> edges;   
//constructing a Graph class function Object() { [native code] } and producing getters and setters
public Graphs(int v)   
{  
Vertex= v;  
edges= new ArrayList<Edge>();  
}  
public int getV()   
{  
return Vertex;  
}  
public void setV(int v)   
{  
Vertex= v;  
}  
public List<Edge> getEdges()   
{  
return edges;  
}  
public void setEdges(List<Edge> edges)   
{  
this.edges = edges;  
}  
public void addEdge(int u, int v, int w)   
{  
Edge e1 = new Edge(u, v, w);  
edges.add(e1);  
}  
}  
class Edge   
{  
//the vertex u is the initial
private int u;   
//the vertex v is the destination vertex
private int v;   
//w denotes the weight of the edge  
private int w;   
//getting and setting getters  
public int getU()   
{  
return u;  
}  
public void setU(int u)   
{  
this.u = u;  
}  
public int getV()   
{  
return v;  
}  
public void setV(int v)   
{  
this.v = v;  
}  
public int getW()   
{  
return w;  
}  
public void setW(int w)   
{  
this.w = w;  
}  
//A constructor was created for the class Edge with the parameters
public Edge(int u, int v, int w)   
{  
this.u = u;  
this.v = v;  
this.w = w;  
}  
}  
//main section of the program
public class BellmanFord 
{  
public static void main(String args[])   
{  
Graphs g1 = createGraphs();  
int distance[] = new int[g1.getV()];  
boolean NegativeCycle = getShortestdistance(g1, 1, distance);  
if(!NegativeCycle)   
{  
System.out.println("VERTEX \t:DISTANCE");      
for(int i = 1; i < distance.length; i++)  
System.out.println("\t"+i + " " + "\t\t"+(distance[i] == Integer.MAX_VALUE ? "-" : distance[i]));  
}   
else   
{  
System.out.println("THE GRAP DOES NOT CONTAIN THE NEGATIVE CYCLES");  
}  
}  
private static Graphs createGraphs()   
{  
int v = 7;  
//A graph g2 having the 7 seven vertices is created  
Graphs g2 = new Graphs(v);  
// the edges are added to the graph g2 
g2.addEdge(1, 2, 4);  
g2.addEdge(1, 4, 9);  
g2.addEdge(2, 3, -1);  
g2.addEdge(3, 6, 3);  
g2.addEdge(4, 3, 2);  
g2.addEdge(4, 5, -5);  
g2.addEdge(5, 6, 0);       
//the function will return th egraph
return g2;  
}  
// logic for bellman ford algorithm 
public static boolean getShortestdistance(Graphs g, int source, int[] distance)   
{  
int Vertex = g.getV();  
// the distance from the source to the other vertices is given 
for(int i = 1; i < Vertex; i++)   
{  
distance[i] = Integer.MAX_VALUE;  
}  
// the source vertex has the initial value as 0
distance[source] = 0;  
// the edges are then relaxed  
for(int i = 1; i < Vertex; i++)   
{  
// by the for loop, the vertices of the graph are iterated     
for(Edge e: g.getEdges())   
{  
int u = e.getU(), v = e.getV(), w = e.getW();  
if(distance[u] != Integer.MAX_VALUE && distance[v] > distance[u] + w)   
{  
// the value of the total distance is calculated     
distance[v] = distance[u] + w;  
}  
}  
}  
//the condition will check whether it contains any negative cycles 
for(Edge e: g.getEdges())   
{  
int u = e.getU(), v = e.getV(), w = e.getW();  
if(distance[u] != Integer.MAX_VALUE && distance[v] > distance[u] + w)   
{  
return true;  
}  
}  
return false;  
} 
} 

Output:

Note:

Numerous graphing programs use negative weights. For instance, if we follow a particular path, we might gain something instead of paying for it.

Fort, he distributed systems, Bellman-Ford performs better (better than Dijkstra's).   Contrary to Dijkstra's, which must determine each vertex's minimum value, Bellman-Ford takes each edge into account individually.

Bellman-Ford cannot solve an undirected network having negative edges because it will be classified as a negative cycle.

Summary

Finding the shortest route through a graph with positive edge weights is an NP-hard problem. There isn't any polynomial-time algorithm for resolving such issues. We can use the Bellman-Ford method in a case where each edge has a negative edge weight.

Cannot use the Bellman-Ford approach to determine the longest simple path between a source (s) and the vertex (v) if the graphs have negative cycles. It's possible to go to a negative-weight cycle from either source. Will stop the algorithm in this situation.