Rehashing in Java
The most crucial idea mostly in the data structure is hashing, which is utilized to change a particular key into some other value. The hash function can be used to create a new value.
In this article, we will comprehend the hashing, load factor, and rehashing concepts in Java.
Rehashing
Rehashing is a method for maintaining the complexity of the get & put operations while dynamically increasing the size of a Map, Array, or Hashtable O(1).
Rehashing, which is the process of recalculating the hash code of the already stored entries and shifting them to a greater size hash map when the map's element counts hit the maximum threshold value, is another definition for the term.
Rehashing, to put it simply, is the opposite of the hashing process. The performance is kept. The load factor is crucial while rehashing.
Load Factor
When to expand the HashMap or Hashtable capacity to keep the get() & put() operations of complexity O is determined by the load factor (1). HashMap's load factor is set by default to 0.75 (or 75% of the map's size). The load factor determines "when and how to increase the number of buckets that store the key-value pair," in other words.
Larger load factor: Higher lookups but less space used.
Smaller load factor: larger space usage compared to the number of pieces needed.
How is the load factor calculated?
The following formula can be used to determine the load factor:
Starting capacity of the HashMap * HashMap load factor
For instance:
HashMap's initial storage size is 16
HashMap's default load factor is 0.75.
16*0.75 equals 12, according to the formula.
It indicates that the HashMap's 12th key-value pair will maintain its 16-bit size. The HashMap will expand from its default size of 24 = 16 buckets to 25 = 32 buckets as soon as the 13th element (key-value pair) is added.
Load factor example
Let's use an illustration to better grasp the load factor.
We are aware that HashMap's default bucket size is 16. After adding the first element, we will determine whether or not we need to extend HashMap's capacity. The formula: can be used to determine it.
HashMap Size (m) / Amount of Buckets (n)
In this instance, our bucket size is 16, and the size of a hashMap is 1. Enough that, 1/16 = 0.0625. Compare the calculated number towards the default load factor now (0.75).
0.0625 < 0.75
The amount is less than the load factor's pre-set value. Therefore, there is no need to expand the HashMap. Consequently, we are not required to expand the HashMap's size to include the 12th entry since
12/16 = 0.75
The resultant number, which is 0.75, is the same as the standard load factor.
The size of the hash map increases as we add the thirteenth entry because:
13/16 = 0.8125
The obtained number in this case is higher than the load factor's default value.
0.8125 > 0.75
The size of the hashMap must be increased in order to add the thirteenth member.
It is suggested to keep your load factor around 0.75 if you want to maintain the O(1) complexity of your get() and put() operations.
Why is rehashing necessary?
When the load factor rises, rehashing is necessary. When we add key-value pairs to the map, both the load factor and the time complexity rise. HashMap typically has an O time complexity (1). We employ the rehashing strategy to lessen HashMap's load factor and temporal complexity.
Why is Rehashing required?
Rehashing becomes necessary when the load factor rises. When we insert a key-value pair into the map, the load factor and time complexity both rise. Typically, HashMap's time complexity is O (1). We employ the rehashing strategy to lessen HashMap's temporal complexity and load factor.
For the following situations, rehashing is recommended:
- halfway through the table.
- whenever the load has reached a particular point (load > 1/2).
- a failed insertion.
- Pick a load factor threshold based on heuristics and evaluated when it is crossed.
Rehashing in Practice
To carry out the rehashing process, the following actions must be taken:
- For each new element that is added to the Map, check the load factor.
- Implementing rehashing becomes necessary if the load factor exceeds its default value of 0.75.
- new double-sized bucketArray to be created
- The insert() method should be called for each element after iterating through the preceding array's (old bucketArray) elements. All of the larger-sized entries in the newly generated bucketArray are added using the insert() method.
Given that there will be a cost associated with rehashing N elements:
O(1)*N + O(N) = O(N)
Rehashing Java Program
Let's use a Java application to implement the rehashing technique.
RehashingExpl.java
import java.util.ArrayList;
class Map<K1, V1>
{
class MapNode<K1, V1>
{
K1 k;
V1 v;
MapNode<K1, V1> next;
// the MapNode class's function Object() { [native code] } being created
public MapNode(K1 k, V1 v)
{
this.k = k;
this.v = v;
next = null;
}
}
// constructing an array of buckets for key-value pairings
ArrayList<MapNode<K1, V1> > buckets;
// The variable n indicates how many pairs are kept
// in the bucket array.
int s;
// variable that indicates the bucket's size Range - b
int numberBuckets;
// establishing the standard loadFactor
final double DEFAULT_LOAD_FACTOR = 0.75;
// creating the constructor for the Map class
public Map()
{
// describing the bucket's dimensions
numberBuckets = 6;
buckets = new ArrayList<>(numberBuckets);
// loop runs for the specified number of bucket
// sizes and initializes nodes to null.
for (int j = 0; j < numberBuckets; j++)
{
// initial bucket contains nothing
buckets.add(null);
}
// outputs all of the initial set values.
System.out.println(" HashMap has created ");
System.out.println(" Pairs in the map, number: " + s);
System.out.println(" Map Size is: " + numberBuckets);
System.out.println(" The Default Load Factor : " + DEFAULT_LOAD_FACTOR + "\n");
}
private int getBucketInd(K1 k)
{
// using the Object class hCode() function to obtain the hash code of the relevant key
int hCode = k.hashCode();
// The array index is calculated, and the same value is returned.
return (hCode % numberBuckets);
}
// constructing a function that adds items to an array
public void insert(K1 k, V1 v)
{
//determining the index where it should be inserted
int bucketInd = getBucketInd(k);
// the index's leading node
MapNode<K1, V1> head = buckets.get(bucketInd);
// In order to determine whether the key already
// exists, the first loop through all of
// the nodes existing at that index.
// The loop iterates over each node displayed
// at a certain index and determines whether or
// not the key has previously been used.
while (head != null)
{
// This value is updated even if the key has already been supplied.
if (head.k.equals(k))
{
head.v = v;
return;
}
head = head.next;
}
// establishing a new key-value pair node
MapNode<K1, V1> newElementNode = new MapNode<K1, V1>(k, v);
// the index's head node
head = buckets.get(bucketInd);
// Making the new node the head
// and the previous head its
// next allows for the insertion
// of the new node.
newElementNode.next = head;
buckets.set(bucketInd, newElementNode);
System.out.println("Pair(" + k + ", " + v + ") has inserted successfully.\n");
// as fresh K-V pairs are added
// to the map, the size increases.
s++;
// the load factor is calculated
double loadFactor = (1.0 * s) / numberBuckets;
System.out.println(" Present Load factor = " + loadFactor);
// Rehashing is carried out if the computed load factor is higher than the default load factor of 0.75.
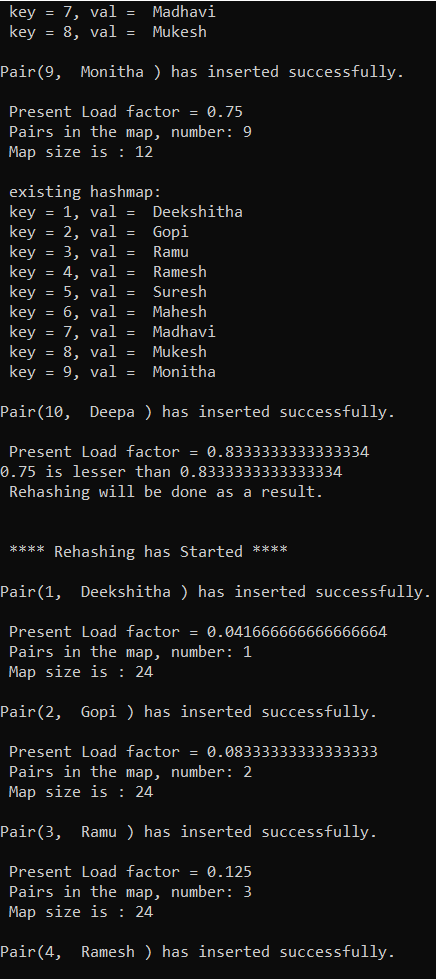
if (loadFactor > DEFAULT_LOAD_FACTOR)
{
System.out.println(DEFAULT_LOAD_FACTOR + " is lesser than " + loadFactor);
System.out.println(" Rehashing will be done as a result.\n ");
// invoking the rehash() method
rehash();
System.out.println(" New size of the map: " + numberBuckets + "\n");
}
System.out.println(" Pairs in the map, number: " + s);
System.out.println(" Map size is : " + numberBuckets + "\n");
}
// Method to perform rehashing
private void rehash()
{
System.out.println("\n **** Rehashing has Started **** \n");
// The current wish list is only meant to be temporary.
ArrayList<MapNode<K1, V1> > temp = buckets;
// making a new bucket list that is twice as
// long as the last one, or (2 * numberBuckets).
buckets = new ArrayList<MapNode<K1, V1> >(2 * numberBuckets);
for (int j = 0; j < 2 * numberBuckets; j++)
{
// all items were initially set to "null"
buckets.add(null);
}
// Now that size has been reduced to zero,
// we loop through each node in the first
// bucket list (temp) and add it to the new list.
s = 0;
numberBuckets = numberBuckets * 2;
for (int j = 0; j < temp.size(); j++)
{
// at that index, the chain's head
MapNode<K1, V1> head = temp.get(j);
while (head != null)
{
K1 k = head.k;
V1 v = head.v;
// since the new list is now a bucketArray,
// inserting each temp node one at a time.
insert(k, v);
head = head.next;
}
}
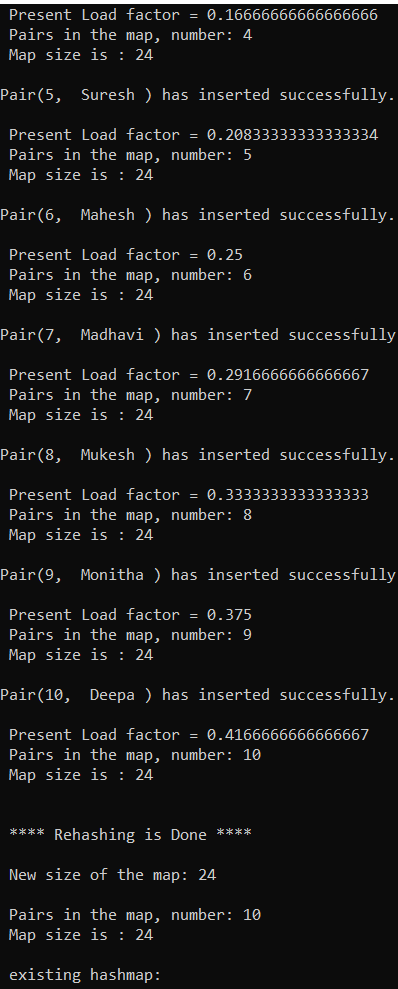
System.out.println("\n **** Rehashing is Done **** \n");
}
// how to print the key-value pairs from the map
public void printMap()
{
// Temporary bucket list is created
ArrayList<MapNode<K1, V1> > temp = buckets;
System.out.println(" existing hashmap: ");
// loop across the Map repeatedly
for (int j = 0; j < temp.size(); j++)
{
// obtaining the temporary bucket list's head index
MapNode<K1, V1> head = temp.get(j);
while (head != null)
{
System.out.println(" key = " + head.k + ", val = " + head.v);
head = head.next;
}
}
System.out.println();
}
}
// main class
public class RehashingExpl
{
public static void main(String args[])
{
// setting up a Map class instance
Map<Integer, String> m = new Map<Integer, String>();
// incorporating items into the Map
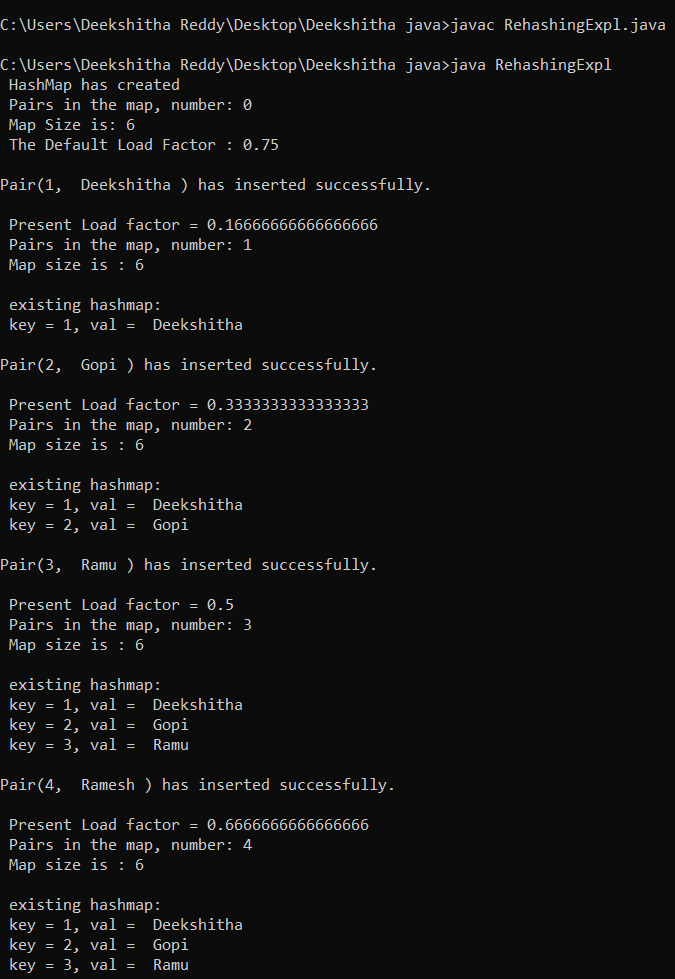
m.insert(1, " Deekshitha ");
m.printMap();
m.insert(2, " Gopi ");
m.printMap();
m.insert(3, " Ramu ");
m.printMap();
m.insert(4, " Ramesh ");
m.printMap();
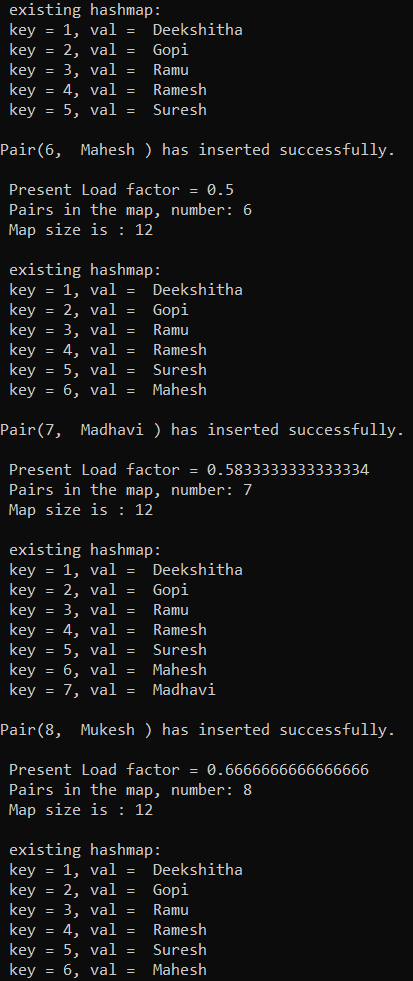
m.insert(5, " Suresh ");
m.printMap();
m.insert(6, " Mahesh ");
m.printMap();
m.insert(7, " Madhavi ");
m.printMap();
m.insert(8, " Mukesh ");
m.printMap();
m.insert(9, " Monitha ");
m.printMap();
m.insert(10, " Deepa ");
m.printMap();
}
}
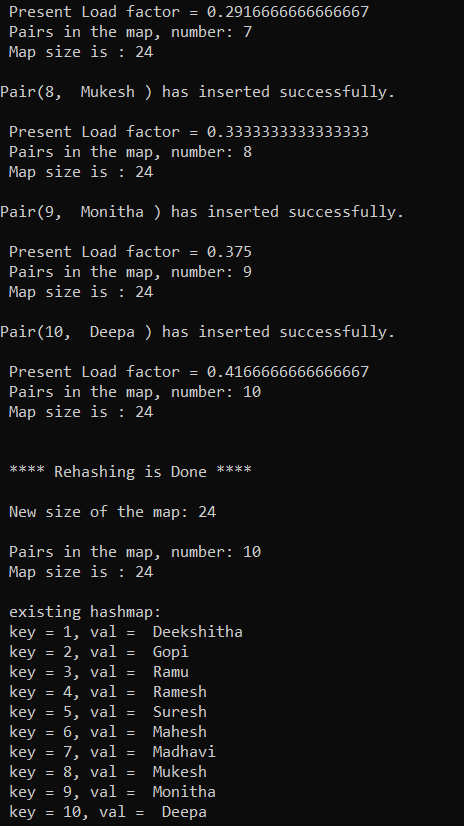
Output: