Powerful Number in Java
We will define a powerful number in this article and write Java programs to determine whether a given number is a powerful number or not. Java coding interviews and academic exams usually involve questions about the powerful number program.
Powerful Number
A number X is referred to as the powerful number if all of its prime divisors and the square of those prime numbers must leave the number X with a zero remainder when divided.
In other words, the factor of the number X must equal the square of all the prime factors of the number X. The form of X must also be l2m3, where l and m are positive integers.
If the following conditions hold for every value of P that is a factor of X: X = l2m3, l > 0, m > 0, X% P = 0, and X% (P * P) = 0, and P is a prime number, then we can claim that X is a powerful number.
If p2 divides a given number n for every prime number p, that number is said to be powerful. For instance, 36 is a powerful number. It is divided by 3 and the square of 3 (i.e., 9).
The initial group of powerful numbers includes:
1, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64 . . . . .
Our objective is to determine whether a given number n is powerful or not.
How to Find the powerful Numbers
Step 1: Assign a number to the variable.
Step 2: Determine the prime factors of the given variable.
Step 3. Store factors in a List.
Step 4: Find the square of the factors in the list as you iterate over them.
Step 5: Determine whether or not each factor in the list has a square that divides the supplied number.
The given number is not a powerful number if the square of any one factor does not divide it.
A number is a powerful number if the prime factor and the square of the prime factor divide the provided number.
Powerful Number Examples
Example 1:
Let us take, X = 15
Factors of X: 3, 5 (prime factors)
Square the prime factors, we get 3 * 3 = 9, and 5 * 5 = 25.
Now, we divide 15 by 9 and 25, respectively.
15 % 9 = 6, and 15 % 25 = 15. Thus, we see remainder is not zero. Hence, the number 15 is not a powerful number.
Example 2:
Let us take, X = 27
Factors of X: 3 (prime factors)
Square of prime factors, we get 3 * 3 = 9.
Divide 27 by 9 we get:
27 % 9 = 0. Thus, we see remainder is zero in every case. Also, 27 can be written as 33, where 3 > 0. Hence, the number 27 is a powerful number.
Example 3:
Let us take, X = 100
Factors of X: 2, 5 (prime factors)
Square of prime factors, we get 2 * 2 = 4 and 5 * 5 = 25.
Now, we divide 100 by 4 and 25, respectively.
100 % 4 = 0, and 100 % 25 = 0. Thus, we see remainder is zero. Hence, the number 100 is a powerful number.
Note: A prime number can never become a powerful number, as the prime factor of the number is the number itself, and the square of the number can never divide the number itself.
Example 4:
Let us take X=5. 5 is a prime number. Hence, its prime factor is also 5. Also, 5 * 5 = 25. Now, 5 % 25 = 5, which is not 0. Hence, 5 is not a powerful number.
Example 5:
Let us take X=7. 7 is a prime number. Hence, its prime factor is also 7. Also, 7 * 7 = 49. Now, 7 % 49 = 7, which is not 0. Hence, 7 is not a powerful number.
Program to find Powerful Number
File name: Pow.java
// Java program to find if a number is powerful or not.
import java.io.* ;
import java.util.* ;
class Pow {
// function to
//determine whether a number is powerful or not
static boolean isPowerful(int p)
{
// First, divide the number.
//by two repeatedly.
while (p % 2 == 0) {
int power = 0 ;
while (p % 2 == 0) {
p /= 2;
power++ ;
}
// Return false if only 2^1 divides n (no higher powers).
if (power == 1)
return false ;
}
// This loop will run if n is not a power of 2.
// re-do the previous steps.
for (int factor = 3; factor <= Math.sqrt(p); factor += 2) {
// Determine the greatest power of the "factor" that divides n.
int power = 0;
while (p % factor == 0) {
p = p / factor;
power++;
}
// Return false if only factor^1 divides n (not higher powers).
if (power == 1)
return false;
}
// Now, if n is not a prime number, it must equal 1.
// We return false if n is not 1 because prime numbers are not powerful numbers.
return (p == 1);
}
// code logic
public static void main(String[] args)
{
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
if (isPowerful(n))
System.out.print("YES\n");
else
System.out.print("NO\n");
}
}Output 1:
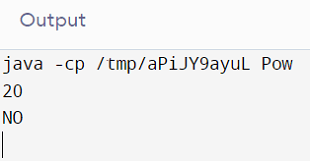
In the above-displayed output, 20 is the given number, and as 20 is not divided by its prime factor's square, 20 is not a powerful number.
Therefore, the program prints “NO”.
Output 2:
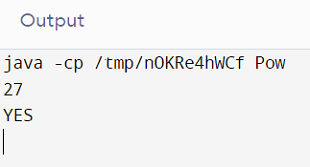
In the above-displayed output, 27 is the given number, and as 27 is divided by its prime factor's square, 27 is a powerful number. The prime factor of 27 is 3, the square of 3 is 9, and 9 divides 27.
Therefore, the program prints “YES”.
Output 3:
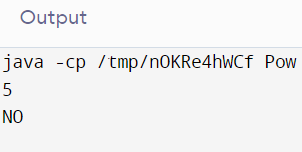
In the above-displayed output, 5 is the given number, and 5 is not divided by its prime factor's square, so 5 is not a powerful number. The prime factor of 5 is 5 itself, the square of 5 is 25, and 25 doesn’t divide 5.
Therefore, the program prints “NO”.
Program to display powerful and not powerful numbers
File name: Pow1.java
// Java program to display powerful numbers and not powerful numbers.
import java.io.* ;
import java.util.* ;
class Pow1 {
// function to determine whether a number is powerful or not
static boolean isPowerful(int p)
{
// First, divide the number
// by two repeatedly.
while (p % 2 == 0) {
int power = 0 ;
while (p % 2 == 0) {
p /= 2 ;
power++ ;
}
// Return false if only 2^1 divides n (no higher powers)
if (power == 1)
return false ;
}
// This loop will run if n is not a power of 2.
// re-do the previous steps.
for (int factor = 3; factor <= Math.sqrt(p); factor += 2) {
// Determine the greatest power of the "factor" that divides n.
int power = 0 ;
while (p % factor == 0) {
p = p / factor ;
power++ ;
}
// Return false if only factor^1 divides n (not higher powers)
if (power == 1)
return false ;
}
// Now, if n is not a prime number, it must equal 1.
// We return false if n is not 1 because prime numbers are not powerful
// numbers.
return (p == 1) ;
}
// code logic
public static void main(String[] args)
{
Scanner sc=new Scanner(System.in) ;
int n=sc.nextInt() ;
for(int i=1;i<=n;i++){
if (isPowerful(i))
System.out.print(i+" is a powerful number\n") ;
else
System.out.print(i+" is not a powerful number\n") ;
}
}
}Output 1:

In the above-displayed output, a range of powerful numbers is displayed. Here, the input is 10, and the program prints the powerful numbers and not powerful numbers from 1 to 10.
The powerful numbers from 1 to 10 are 1, 4, 8, and 9.
Output 2:

In the above-displayed output, a range of powerful numbers is displayed. Here, the input is 20, and the program prints the powerful numbers and not powerful numbers from 1 to 20.
The powerful numbers from 1 to 10 are 1, 4, 8, 9, and 16.
Program to find powerful numbers in a given range
File name: Pow2.java
// Java program to find only the powerful numbers.
import java.io.* ;
import java.util.* ;
class Pow2 {
// function to
//determine whether a number is powerful or not
static boolean isPowerful(int p)
{
// First, divide the number
//by two repeatedly.
while (p % 2 == 0) {
int power = 0;
while (p % 2 == 0) {
p /= 2;
power++ ;
}
// Return false if only 2^1 divides n (no higher powers)
if (power == 1)
return false ;
}
// This loop will run if n is not a power of 2.
// re-do the previous steps.
for (int factor = 3; factor <= Math.sqrt(p); factor += 2) {
// Determine the greatest power of the "factor" that divides n.
int power = 0;
while (p % factor == 0) {
p = p / factor;
power++ ;
}
// Return false if only factor^1 divides n (not higher powers)
if (power == 1)
return false ;
}
// Now, if n is not a prime number, it must equal 1.
// We return false if n is not 1 because prime numbers are not powerful
// numbers.
return (p == 1) ;
}
// code logic
public static void main(String[] args)
{
Scanner sc=new Scanner(System.in) ;
int n=sc.nextInt();
System.out.print("Powerful numbers : ") ;
for(int i=1;i<=n;i++){
if (isPowerful(i))
System.out.print(i+" ") ;
}
}Output:
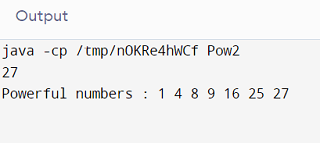
The above-displayed output displays a range of powerful numbers from 1 to 27.