Zigzag Traversal of Binary Tree in Java
In this article, you will be acknowledged about the zigzag traversal of binary tree in java and the approaches or ways in which the zigzag traversal can be done.
Zigzag Traversal
A binary tree is traversed in a zigzag pattern, which means that for each node at the top level, we move from left to right, and for the node at the next level, we move from right to left, and on and on. Be aware that while going to the next level requires going from left to right, the top level allows us to go from right to left rather than left to right. The crucial thing to keep in mind when performing a zigzag traverse of just a binary tree in Java that each level's traversal direction is the opposite of the level before it.
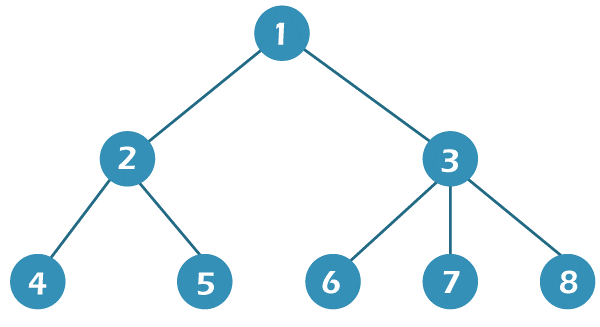
In the above binary tree with the given nodes, the two types of zigzag traversal path is
Right Traversal: 1 3 2 8 7 6 5 4
Left Traversal: 1 2 3 4 5 6 7 8
There are 4 ways that can achieve zigzag traversal in a simple binary tree. They are
- Making use of Two Stacks
- With Deque
- Leveraging Recursion
- Stack and Queue utilization
Making use of two stacks
Two stacks can be used to traverse a binary tree in a zigzag pattern. You should consider the first stack to be actual level stack and also the second stack to be the next level stack. In order to obtain information on the current level order, a variable is also necessary. We actually pop nodes out of actual level stack and show their values. When traversing the actual level order from left to right, we push the level's left child to the next level stack first, followed by the level's right child. We are aware that a stack operates according to the Last In First Out (LIFO) rule.
As a result, the sequence of traversing will be reversed the next time nodes are taken off of the nextlevel stack. Similar to how we move the right child of a current node before the left child while traversing from right to left. Keep in mind that we must switch the stacks once each level ends (which occurs when all of that level's nodes have been explored); that is, the next-level stack becomes the current-level stack, and vice versa.
Let us understand it with an example program
File name: Zigzag1.java
import java.util.*;
class TreeNode
{
int val;
TreeNode left, right;
public TreeNode(int i)
{
val = i;
right = left = null;
}
}
class BTZigZag
{
TreeNode r;
//method that shows the zigzag traversal in a binary tree
void displayZigZagTraversal()
{
if (r == null)
{
return;
}
//Initializing the two stacks
Stack<TreeNode> currLevel = new Stack<TreeNode>();
Stack<TreeNode> nextLevel = new Stack<TreeNode>();
currLevel.push(r);
boolean LtoR = true;
while (!currLevel.isEmpty())
{
//The node has been removed from the current level
TreeNode currNode = currLevel.pop();
System.out.print(currNode.val + " ");
if (LtoR)
{
if (currNode.left != null)
{
nextLevel.push(currNode.left);
}
if (currNode.right != null)
{
nextLevel.push(currNode.right);
}
}
else
{
if (currNode.right != null)
{
nextLevel.push(currNode.right);
}
if (currNode.left != null)
{
nextLevel.push(currNode.left);
}
}
if (currLevel.isEmpty())
{
// toggle the value of LtoR
LtoR = !LtoR;
Stack<TreeNode> stk = currLevel;
currLevel = nextLevel;
nextLevel = stk;
}
}
}
}
public class ZigZag1
{
// main method
public static void main(String[] args)
{
BTZigZag
BTZigZag tree = new BTZigZag ();
//the root node
tree.r = new TreeNode(10);
//The other nodes of the tree are
tree.r.left = new TreeNode(6);
tree.r.right = new TreeNode(15);
tree.r.left.left = new TreeNode(5);
tree.r.left.right = new TreeNode(8);
tree.r.right.left = new TreeNode(11);
tree.r.right.right = new TreeNode(23);
tree.r.left.left.left = new TreeNode(12);
tree.r.left.left.right = new TreeNode(16);
tree.r.left.right.left = new TreeNode(9);
tree.r.left.right.right = new TreeNode(19);
tree.r.right.left.left = new TreeNode(17);
tree.r.right.left.right = new TreeNode(29);
tree.r.right.right.left = new TreeNode(33);
tree.r.right.right.right = new TreeNode(36);
System.out.println("The nodes in the form of zigzag traversal : ");
tree.displayZigZagTraversal();
}
}
Output:
The nodes in the form of zigzag traversal
10 6 15 5 8 11 23 12 16 9 19 17 29 33 36 Time Complexity
The program contains just one while loop. As a result, the preceding programme has an O(n) time complexity, where n represents the total amount of nodes as in binary tree.
Space Complexity
The code contains two stacks, each of which has an O(n) space complexity, where n corresponds to the total count of nodes in the binary tree. As a result, O(2 * n), which is equal to O in terms of exponential growth complexity (n).
Using Deque
A deque can be used to perform a binary tree's zigzag traverse as well. Choosing whether to do the pop operation from the front or the back side is a crucial consideration. Whether we move from right to left or from left to right is determined by the pop operation.
Let us understand it with an example program by using deque operation in queue.
File name: Zigzag2.java
import java.util.*;
class TreeNode
{
//holds the nodes values
int val;
//Linking all the nodes left nodes for the left and right nodes for the right nodes
TreeNode left, right;
//The initialization of class fields in done with help of a constructor
public TreeNode(int i)
{
val = i;
right = left = null;
}
}
class BTreeZigZag1
{
TreeNode r;
//This method helps in showing the zigzag traversal
public Vector<Integer> zigZagTraversal(TreeNode node)
{
Deque<TreeNode> dq = new LinkedList<TreeNode>();
Vector<Integer> vec = new Vector<Integer>();
dq.add(node);
vec.add(node.val);
TreeNode t;
int lvl = 1;
while (dq.size() > 0)
{
int n = dq.size();
for (int j = 0; j < n; j++)
{
if (lvl % 2 == 0)
{
t = dq.peekLast();
// deleting from the end
dq.pollLast();
}
else
{
t = dq.peekFirst();
dq.pollFirst();
}
// The left child node is followed by the right child node when the level is odd
// The right child node is followed by the left child node when the level is even
if (lvl % 2 != 0)
{
// The null nodes are found to be useless because they do not have any child nodes
if (t.right != null)
{
dq.add(t.right);
vec.add(t.right.val);
}
if (t.left != null)
{
dq.add(t.left);
vec.add(t.left.val);
}
}
else if (lvl % 2 == 0)
{
// // The null nodes are found to be useless because they do not have any child nodes
if (t.left != null)
{
dq.offerFirst(t.left);
vec.add(t.left.val);
}
if (t.right != null)
{
dq.offerFirst(t.right);
vec.add(t.right.val);
}
}
}
lvl = lvl + 1;
}
return vec;
}
}
public class Zigzag2
{
public static void main(String[] args)
{
BTZigZag1 tree = new BTZigZag1 ();
tree.r = new TreeNode(10);
tree.r.left = new TreeNode(6);
tree.r.right = new TreeNode(15);
tree.r.left.left = new TreeNode(5);
tree.r.left.right = new TreeNode(8);
tree.r.right.left = new TreeNode(11);
tree.r.right.right = new TreeNode(23);
tree.r.left.left.left = new TreeNode(12);
tree.r.left.left.right = new TreeNode(16);
tree.r.left.right.left = new TreeNode(9);
tree.r.left.right.right = new TreeNode(19);
tree.r.right.left.left = new TreeNode(17);
tree.r.right.left.right = new TreeNode(29);
tree.r.right.right.left = new TreeNode(33);
tree.r.right.right.right = new TreeNode(36);
System.out.println("The nodes in the form of zigzag traversal are: ");
Vector<Integer> vec = tree.zigZagTraversal(tree.r);
for (int j = 0; j < vec.size(); j++)
{
//printing the nodes in zigzag way
System.out.print(vec.get(j) + " ");
}
}
} Output
The nodes in the form of zigzag traversal are:
10 15 6 23 11 8 5 36 33 29 16 19 9 16 12Time complexity
The temporal complexity of the aforementioned code is O(n), in which n is the overall number of nodes in the binary tree, because we only visit each node once.
Space complexity
The largest size of the deque is O((n + 1) / 2), which has an asymptotic complexity equal to O(n), in which n refers to the overall number of nodes in the binary tree. Consider that the overall quantity of subtrees in a complete binary tree is (n + 1) / 2.
Using Leveraging Recursion
Recursion can also be used to traverse a binary tree in a zigzag pattern. The idea is to leveraging a binary tree's level order traversal in a novel way. A parameter whose value alternates between 0 and 1 will establish the path in which the traversing will proceed. Keep in mind that the variable's value modifies following the conclusion of each level's exploration.
Let us understand it with an example program by using the recursion methodology.
File name: Zigzag3.java
import java.util.*;
class TreeNode
{
//For the value of node to be assigned
int val;
TreeNode left, right;
//The class fields are created by the constructor
public TreeNode(int i)
{
val = i;
right = left = null;
}
}
class BTreeZigZag2
{
TreeNode r;
// The length of the tree is found by the recursion approach
//The important point is that all the levels of binary tree must be equal
public int heightOfBTree(TreeNode r)
{
if(r == null)
{
return 0;
}
int lh = heightOfBTree(r.left);
int rh = heightOfBTree(r.right);
return Math.max(lh + 1, rh + 1);
}
//This method displays the values of nodes from the right to left
public void displayRightToLeft(TreeNode r, int lvl)
{
if(r == null)
{
return;
}
if(lvl == 1)
{
System.out.print(r.val + " ") ;
}
else if(lvl > 1)
{
displayRightToLeft(r.right, lvl - 1);
displayRightToLeft(r.left, lvl - 1);
}
}
//This method displays the values of nodes from left to right
public void displayLeftToRight(TreeNode r, int lvl)
{
if(r == null)
{
return;
}
if(lvl == 1)
{
System.out.print(r.val + " ");
}
//This is for managing the other nodes of the binary tree.
else if(lvl > 1)
{
displayLeftToRight(r.left, lvl - 1);
displayLeftToRight(r.right, lvl - 1);
}
}
//This method displays the nodes of binary tree in zigzag traversal
public void displayZigZagTraversal(TreeNode r)
{
int f = 0;
//Length of the binary tree
int ht = heightOfBTree(r);
for(int j = 1; j <= ht; j++)
{
//The nodes values are displayed from right to left if the flag value is one
if(f == 1)
{
displayRightToLeft(r, j);
f = 1 - f;
}
// The nodes values are displayed from right to left if the flag value is one
else if(f == 0)
{
displayLeftToRight(r, j);
f = 1 - f;
}
}
}
}
public class Zigzag3
{
public static void main(String[] argvs)
{
BTZigZag2 tree = new BTZigZag2();
tree.r = new TreeNode(10);
tree.r.left = new TreeNode(6);
tree.r.right = new TreeNode(15);
tree.r.left.left = new TreeNode(5);
tree.r.left.right = new TreeNode(8);
tree.r.right.left = new TreeNode(11);
tree.r.right.right = new TreeNode(23);
tree.r.left.left.left = new TreeNode(12);
tree.r.left.left.right = new TreeNode(16);
tree.r.left.right.left = new TreeNode(9);
tree.r.left.right.right = new TreeNode(19);
tree.r.right.left.left = new TreeNode(17);
tree.r.right.left.right = new TreeNode(29);
tree.r.right.right.left = new TreeNode(33);
tree.r.right.right.right = new TreeNode(36);
System.out.println("The nodes in the from of zigzag traversal are: ");
tree.displayZigZagTraversal(tree.r);
}
}Output
The nodes in the form of zigzag traversal are
10 15 6 23 11 8 5 36 33 29 16 19 9 16 12
Time Complexity
The preceding program's time complexity is O(n), where n is the overall number of nodes in the binary tree, and we are only visiting each node once.
Space Complexity
The above-mentioned program's space complexity is O (n).
Using Stack and Queue utilization
This method involves traversing the level order, but not always in the same direction. When moving through a level from left to right, we add every node we come across to the array list maintain. Additionally, we keep the connections for the following level of the stack. We push the node out from stack which had been saved in the preceding stage while travelling from right to left. The array list retain contains the popped node. Finally, we deliver the array list maintain. Keep in mind that the method we employed for this approach's optimization was deque.
Let us understand it with an example program by using the recursion methodology.
File name: Zigzag4.java
import java.util.*;
class TreeNode
{
int val;
TreeNode left, right;
public TreeNode(int i)
{
val = i;
right = left = null;
}
}
public class Zigzag4
{
TreeNode r = null;
ArrayList<Integer> zigzagLevelOrderTraversal(TreeNode root)
{
ArrayList<Integer> keep = new ArrayList<Integer>();
Queue<TreeNode> nodes = new LinkedList<TreeNode>();
Stack<TreeNode> currentLevelNodes = new Stack<TreeNode>();
nodes.add(root);
int ltor = 1;
while (!nodes.isEmpty())
{
if (ltor == 1)
{
int size = nodes.size();
for (int j = 0; j < size; j++)
{
TreeNode currNode = nodes.peek();
nodes.poll();
keep.add(currNode.val);
if (currNode.left != null)
{
nodes.add(currNode.left);
currentLevelNodes.push(currNode.left);
}
if (currNode.right != null)
{
nodes.add(currNode.right);
currentLevelNodes.push(currNode.right);
}
}
}
else
{
int size = nodes.size();
for (int j = 0; j < size; j++)
{
TreeNode currentNode = nodes.peek();
nodes.poll();
keep.add(currentLevelNodes.peek().val);
currentLevelNodes.pop();
if (currentNode.left != null)
{
nodes.add(currentNode.left);
}
if (currentNode.right != null)
{
nodes.add(currentNode.right);
}
}
}
ltor = 1 - ltor;
}
return keep;
}
public static void main(String[] argvs)
{
Zigzag4 tree = new Zigzag4();
tree.r = new TreeNode(10);
tree.r.left = new TreeNode(6);
tree.r.right = new TreeNode(15);
tree.r.left.left = new TreeNode(5);
tree.r.left.right = new TreeNode(8);
tree.r.right.left = new TreeNode(11);
tree.r.right.right = new TreeNode(23);
tree.r.left.left.left = new TreeNode(12);
tree.r.left.left.right = new TreeNode(16);
tree.r.left.right.left = new TreeNode(9);
tree.r.left.right.right = new TreeNode(19);
tree.r.right.left.left = new TreeNode(17);
tree.r.right.left.right = new TreeNode(29);
tree.r.right.right.left = new TreeNode(33);
tree.r.right.right.right = new TreeNode(36);
System.out.println("The nodes in the form of zigzag traversal are: ");
ArrayList<Integer> list = tree.zigzagLevelOrderTraversal(tree.r);
for(int i = 0; i < list.size(); i++)
{
System.out.print(list.get(i) + " ");
}
}
}
Output
The nodes in the form of zigzag traversal are
10 15 6 23 11 8 5 36 33 29 16 19 9 16 12Time complexity
The binary tree's total amount of nodes, n, corresponds to the time complexity, which is O(n).
Space complexity
The above-mentioned program's space complexity is O (n).