Three Partition Problems in Java
In talks with leading IT organizations like Google, Amazon, TCS, Accenture, etc., this extremely intriguing subject is constantly brought up. The goal of the problem-solving exercise is to evaluate the interviewee's logical reasoning, critical thinking, and problem-solving abilities. Therefore, we will solve the three partition problems in Java using various strategies and logic in this section. Additionally, we'll write Java programs for the same.
Problem Statement
There is a list of positive numbers. It is our job to determine the extent to which the input array can be divided into three fully distinct subsets so that the sum of each of the elements in one subset equals the sum of each of the elements in the other subset. Keep in mind that the input array must contain every element. Show the proper messages just on the console in accordance.
Example 1:
Input
int inputArr[] = {3, 7, 6, 4, 2, 8}
Output: Three separate subsets with an equal number of elements each can be created from the input array that is given.
Consider the following subsets, for clarification.
Sum of Subset1 = "3, 7" is 3 + 7 = 10, Subset2 = 6,4 total = 6 + 4 equals 10,
Sum = 2 + 8 = 10 for subset3 = "2, 8"
As a result, it is clear that we received three equal-sized subsets of the items.
Example 2:
Input
int inputArr[] = {6, 2, 3, 9, 8, 18, 96}
Output: It is impossible to divide the input array into three separate subsets that each have the same number of elements.
Reason: For the specified input array, no set of three subsets will produce an equal number of elements.
Recursive Methodology
First, we'll determine whether the input array's total number of elements is indeed a multiple of three or not. The partition cannot be done if the number is not a multiple of 3. If so, we must determine whether or not three disjoint sets exist were the sum of elements was equal to (the total sum of the input array's elements) / 3. It can be discovered by carefully examining each component of an input array individually. You have the following three options for each element:
- Take into account the element from the first subset before recursively finding the other elements.
- Take into account the component of the second subset and use recursion on the other components.
- Recursion is used to find the other elements after taking into account an element for such a third subset. The test scenario of the recursion will indeed be reached when all of the input array's items have been taken into account because we must take into account every item. Whenever three disjoint subsets were discovered, the recursion may return true.
ThreePartitionExpl1.java
public class ThreePartitionExpl1
{
// An aid for solving the three-partition problem.
// There are three disjoint subsets with both the
// total if it returns true.
public boolean disjointSubsetSum(int a[], int s, int j, int k, int l)
{
// if the subgroup is found, return true.
if (j == 0 && k == 0 && l == 0)
{
return true;
}
// handling the simplest scenario: removing all objects
if (s < 0)
{
return false;
}
// Case 1: The present element is contained in the first subset.
boolean case1 = false;
if (j - a[s] >= 0) {
case1 = disjointSubsetSum(a, s - 1, j - a[s], k, l);
}
// Case 2: The present element is contained in the second subset.
boolean case2 = false;
if (!case1 && (k - a[s] >= 0))
{
case2 = disjointSubsetSum(a, s - 1, j, k - a[s], l);
}
// Case 3: The present element is contained in the third subset.
boolean case3 = false;
if ((!case1 && !case2) && (l - a[s] >= 0))
{
case3 = disjointSubsetSum(a, s - 1, j, k, l - a[s]);
}
// We can return true if any one of the three scenarios is true.
return case1 || case2 || case3;
}
// a formula for solving the three
// partitions problem. If the given
// set a[0... n - 1] can be divided
// into the set of three disjoint
// subsets that have the same total,
// the function returns true.
public boolean partitionInThree(int a[])
{
// It follows that the supplied array
// must have at least three members for
// each of the three disjoint subgroups.
if (a.length < 3)
{
return false;
}
// find the total of all the elements in the specified array.
int sumOfElements = 0;
for(int j = 0; j < a.length; j++)
{
sumOfElements = sumOfElements + a[j];
}
// return true if the input array can be
// partitioned into three disjoint subsets
// with equal sums and the sum of all of the
// elements have been divisible by three.
if((sumOfElements % 3) == 0)
{
if (disjointSubsetSum(a, a.length - 1, sumOfElements / 3, sumOfElements / 3, sumOfElements / 3))
{
return true;
}
return false;
}
return false;
}
// Driver code
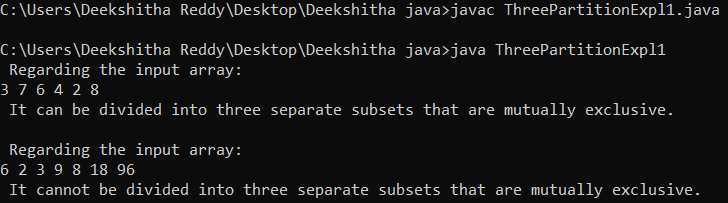
public static void main(String args[])
{
// creating an instance for the class
ThreePartitionExpl1 o = new ThreePartitionExpl1();
// First input
int a[] = {3, 7, 6 , 4 , 2 , 8};
int s = a.length;
System.out.println(" Regarding the input array: ");
for(int j = 0; j < s; j++)
{
System.out.print(a[j]+ " ");
}
System.out.println();
if (o.partitionInThree(a))
{
System.out.println(" It can be divided into three separate subsets that are mutually exclusive.");
}
else
{
System.out.println(" It cannot be divided into three separate subsets that are mutually exclusive.");
}
System.out.println();
// second input
int a2[] = {6, 2, 3, 9, 8, 18, 96};
s = a2.length;
System.out.println(" Regarding the input array: ");
for(int j = 0; j < s; j++)
{
System.out.print(a2[j]+ " ");
}
System.out.println();
if (o.partitionInThree(a2))
{
System.out.println(" It can be divided into three separate subsets that are mutually exclusive.");
}
else
{
System.out.println(" It cannot be divided into three separate subsets that are mutually exclusive.");
}
}
}
Output:
Analysis of Complexity: The program mentioned above has exponential time complexity.
The aforementioned application produces the desired results; however, it takes a long time. As a result, it cannot effectively handle a huge input.
Using Dynamic Programming
With the use of dynamic programming, we can lessen the temporal complexity. Take note of the program below.
ThreePartitionExpl2.java
import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
class ThreePartitionExpl2
{
// aid in resolving the three partition problem.
// If there are three subsets with both the
// specified total, it returns true.
public static boolean subsetSum(int[] S1, int n1, int a1, int b1, int c1,
Map<String, Boolean> h1)
{
// if the subgroup is found, return true.
if (a1 == 0 && b1 == 0 && c1 == 0) {
return true;
}
// base scenario: nothing is left
if (n1 < 0) {
return false;
}
// create a distinct map key from dynamic input components.
String key = a1 + "|" + b1 + "|" + c1 + "|" + n1;
// Solve the subproblem if it
// appears for the very first time,
// then save the solution in a map.
if (!h1.containsKey(key))
{
// Case 1. The current item joins the first subset.
boolean case1 = false;
if (a1 - S1[n1] >= 0) {
case1 = subsetSum(S1, n1 - 1, a1 - S1[n1], b1, c1, h1);
}
// Case 2. The current item joins the second subset.
boolean case2 = false;+
if (!case1 && (b1 - S1[n1] >= 0)) {
case2 = subsetSum(S1, n1 - 1, a1, b1 - S1[n1], c1, h1);
}
// Case 3. The current item joins the third subset.
boolean case3 = false;
if ((!case1 && !case2) && (c1 - S1[n1] >= 0)) {
case3 = subsetSum(S1, n1 - 1, a1, b1, c1 - S1[n1], h1);
}
// return true when we are successful.
h1.put(key, case1 || case2 || case3);
}
// bring back the map's subproblem resolution
return h1.get(key);
}
// Function to solve the three-partitioning puzzle.
// If the supplied set "S" can be partitioned into
// three subsets with just an equal sum, then it returns "true."
public static boolean partition(int[] S1)
{
if (S1.length < 3) {
return false;
}
// make a map to keep answers to a subproblem.
Map<String, Boolean> h1 = new HashMap<>();
// find the total of all the set's elements
int s = Arrays.stream(S1).sum();
// if the total is divisible by three and
// the set "S" can be partitioned into
// three subsets with equal sums, then return true.
return (s % 3) == 0 && subsetSum(S1, S1.length - 1, s/3,
s/3, s/3, h1);
}
public static void main(String[] args)
{
// Input: a set of integers
int[] S1 = { 7, 3, 2, 1, 5, 4, 8 };
if (partition(S1)) {
System.out.println(" Set may be divided. ");
}
else {
System.out.println(" Set may not be divided. ");
}
}
}
Output:

Complexity analysis: The running time of the aforementioned program is O(sum3 n) and it also uses extra space of O(sum3 n), where the sum is indeed the sum of all the input array's elements and n is the array's total number of elements.
The Problem's Expansion
To print all three disjoint subsets with sums that are equal is another question an interviewer might ask. The items of the disjoint subset must be tracked by an array in this case. Watch the program that comes next.
// ThreePartitionExpl3.java
public class ThreePartitionExpl3
{
// An aid for solving the three-partition problem.
// There are three disjoint subsets with both the
// total if it returns true.
public boolean disjointSubsetSum(int a[], int s, int j, int k, int l, int store[])
{
// if the subgroup is found, return true.
if (j == 0 && k == 0 && l == 0)
{
return true;
}
// handling the simplest scenario: removing all objects
if (s < 0)
{
return false;
}
// Case 1: The current element is contained in the first subset.
boolean case1 = false;
if (j - a[s] >= 0)
{
// tracking the current component. 1 denotes the initial subset.
store[s] = 1;
case1 = disjointSubsetSum(a, s - 1, j - a[s], k, l, store);
}
// Case 2: The current element is contained in the second subset.
boolean case2 = false;
if (!case1 && (k - a[s] >= 0))
{
// tracking the current component. 2 denotes the second subset.
store[s] = 2;
case2 = disjointSubsetSum(a, s - 1, j, k - a[s], l, store);
}
// Case 3: The current element is contained in the third subset.
boolean case3 = false;
if ((!case1 && !case2) && (l - a[s] >= 0))
{ // tracking the current component. 3 denotes the third subset.
store[s] = 3;
case3 = disjointSubsetSum(a, s - 1, j, k, l - a[s], store);
}
return (case1 || case2 || case3) ;
}
// a formula for solving the three partitions problem.
// If the given set a[0... n - 1] can be divided
// into a series of three disjoint subsets that have
// the same total, the function returns true.
public boolean partitionInThree(int a[], int s[])
{
// For the three disparate subsets, it is evident.
// The provided array must include at least three elements.
if (a.length < 3)
{
return false;
}
// find the total of all the elements in the specified array.
int sumOfElements = 0;
for(int j = 0; j < a.length; j++)
{
sumOfElements = sumOfElements + a[j];
}
// return true if the input array can be partitioned
// into three disjoint subsets with equal sums and the
// sum of all of the elements is divisible by three.
if((sumOfElements % 3) == 0)
{
if (disjointSubsetSum(a, a.length - 1, sumOfElements / 3, sumOfElements / 3, sumOfElements / 3, s))
{
return true;
}
return false;
}
return false;
}
void display(int a[], int s[])
{
// the dividers in print
for (int k = 0; k < 3; k++)
{
System.out.print(" Partition " + k + " is ");
for (int l = 0; l < a.length; l++)
{
if (s[l] == k + 1) {
System.out.print(a[l] + " ");
}
}
System.out.println();
}
}
// driver code
public static void main(String args[])
{
// creating an instance for the class
ThreePartitionExpl3 o = new ThreePartitionExpl3();
// first input
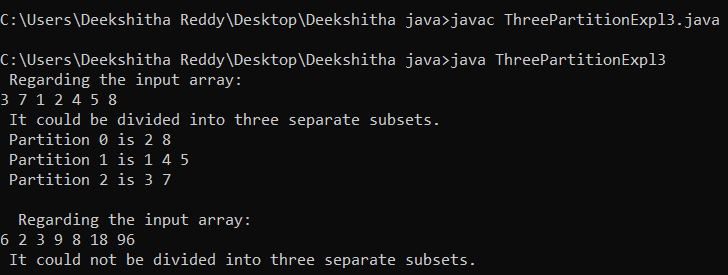
int a[] = {3, 7, 1, 2, 4, 5, 8};
int s = a.length;
// to keep track of the components of both the disjoint subsets
int[] store = new int[a.length];
System.out.println(" Regarding the input array: ");
for(int j = 0; j < s; j++)
{
System.out.print(a[j]+ " ");
}
System.out.println();
if (o.partitionInThree(a, store))
{
System.out.println(" It could be divided into three separate subsets. ");
o.display(a, store);
}
else
{
System.out.println(" It could not be divided into three separate subsets. ");
}
System.out.println();
// second input
int a2[] = {6, 2, 3, 9, 8, 18, 96};
s = a2.length;
System.out.println(" Regarding the input array: ");
for(int j = 0; j < s; j++)
{
System.out.print(a2[j]+ " ");
}
System.out.println();
if (o.partitionInThree(a2, store))
{
System.out.println(" It could be divided into three separate subsets. ");
}
else
{
System.out.println(" It could not be divided into three separate subsets. ");
}
}
}
Output: