Java Binary Tree

The non-linear data structure known as a binary tree is a type of tree, and because it stores data in a hierarchical manner, it is mostly utilised for finding and sorting. We will study the Java implementation of the data structure for binary trees in this section. It gives a concise summary of data structure for binary trees as well.

Binary Tree

Binary trees are trees in which each parent node only has two children (left and right) at most. The root node is the highest node. Each node in a binary tree has data and a pointer (address) to the left and right child nodes.

The formula below can be used to determine the number of nodes and leaves.

• The most leaf nodes a binary tree can have are 2h.
• The most nodes a binary tree can have are 2h+1-1.

where h is the binary tree's height.

Binary Tree Types:

The following categories of binary trees are used in data structures:

1. Full or Strictly Binary tree
2. Complete Binary tree
3. Perfect Binary tree
4. Balance Binary tree
5. Rooted Binary tree
6. Pathological Binary tree or Degenerated
7. Extended Binary tree
8. Skewed Binary tree
   • Left-skewed Binary tree
   • Right-skewed Binary tree
9. Threaded Binary tree
   • Single Threaded Binary tree
   • Double threaded Binary tree

Java implementation of a binary tree

Binary tree can be implemented in a variety of ways. In this part, we'll use the LinkedList data structure to create a binary tree. In addition to that, we will also put the traversal orders into practise, search a node, and add a node to a binary tree.

Binary Tree Implementation Using LinkedList

Algorithm

Create a node class with the following three attributes: data left, data right. Left here indicates the node's left child, and right here represents the node's right child.

• Data is passed to the node's data attribute at creation, and left and right are both set to null.
• Define a different class with a root attribute.
• Initialize Root to null to represent the tree's root node.
• A new node will be added to the tree via insert().
  • It determines if the root is null, which indicates that the tree is empty. The new node will become root after that.
  • If not, root will be added to the queue.
  • The current node is represented by the variable node.
  • It first determines if a node has both a left and a right child. If so, both nodes will be added to the queue.
  • The new node will be added as the left child if the left child is absent.
  • The right child of the new node will be added if the left is present.
• The tree's nodes will be displayed in order via inorder().
  • The complete tree is traversed before printing the left child, the root, and then the right child.

1) Fully or Strictly Binary tree

A rigorous binary tree is another name for the full binary tree. Only if each node has either 0 or 2 offspring can the tree be regarded as a full binary tree. The term "complete binary tree" can also refer to a tree where all nodes, excluding the leaf nodes, must have two children.

The Full Binary Tree's Characteristics:

• One more than the amount of internal nodes makes up the number of leaf nodes. Given that there are 5 internal nodes in the example above, there are also 6 leaf nodes.
• The maximum number of nodes is 2h+1-1, which corresponds to the number of nodes in the binary tree.
• The whole binary tree must have at least 2*h-1 nodes.
• The whole binary tree has a minimum height of log2(n+1) - 1.
• The entire binary tree's maximum height can be calculated using the formula:

n= 2*h - 1

n+1 = 2*h

h = n+1/2

2) Complete Binary Tree

The last level of the entire binary tree is the only level that does not have any empty nodes. Every node in the final level must be as far to the left as feasible. A complete binary tree should have its nodes inserted from the left.

Let's construct a whole binary tree.

With the exception of the lowest level nodes, which are filled from the left as much as feasible, all levels of a complete binary tree are fully filled.

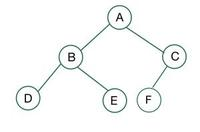
Components of Binary Tree:

• Root - Node where the parent is not the source of any edges. Case Study: Node A
• Child - A node that has an incoming edge is said to be a kid. For instance, nodes B and H are the offspring of A and D, respectively.
• Sibling - Nodes that share a parent are considered siblings. For instance, J and K are related because they share the same parent, E.
• Degree of a node - number of kids a certain parent has. For instance, Degree A is 2 while Degree H is 1. Degree L is zero.
• Internal/External nodes - External nodes are leaf nodes, while internal nodes are those that lack leaves.
• Level - A path to a target node's nodes can be counted. Using the nodes A, D, and H as an example, the level of node H is 3.
• Height - Reaching Root, the final node, requires zero edges and is located at height. Example: Node E has two edges coming from the root, making it two nodes tall.

The complete binary tree's characteristics:

• A suitable binary tree, where every leaf has the same depth, is referred to as a complete binary tree.
• In a full binary tree, there are 2d nodes at depth d.
• The height of a fully-connected binary tree with n nodes is equal to log(n+1).
• All levels - all but the final one - are entirely full.

Optimal binary tree versus Full binary tree

A binary tree that has the most nodes and is height "h" is said to be ideal.

The most nodes are 2h+1-1 for a height h provided.

In a binary tree of height h, all of the elements are stored in left to right order up until the height h-1 proper binary tree.

3) Balance binary tree:

Height balanced tree is another name for a balanced binary tree. When the heights of the left and right subtrees differ by no more than m, which is often equal to 1, it is said to be a binary tree.

Binary search is used to create the tree shown above. In a binary search tree, each node on the left side is less significant than its parent node, while the node on the right side is more significant than its parent node. The leaf nodes in the tree above are numbered n4, n6, and n 7, whereas node 1 is the root. The node that is located the furthest away from the root node is n7. In addition to the three edges between the root node and the n7 node, the n4 and n6 both have two edges. The above tree is three feet tall because node n7 is the furthest away from the root node.

We'll now check to see if the tree is balanced or not. The nodes n2, n4, n5, and n7 are found in the left subtree, while n3 and n6 are found in the right subtree. Two leaf nodes, numbered n4 and n7, make up the left subtree. The node n7 is the furthest away from the root node since there is just one edge connecting nodes n2 and n4, and two edges connecting nodes n7 and n2.

The left subtree is 2 in height. The right subtree's height is 1 because it has just one edge and one leaf node, which is n6, respectively. We may argue that the aforementioned tree is a height-balanced tree because we received the value 1. Each node, such as n2, n3, n4, n5, n6, and n7, should go through this procedure of computing the height difference. We may argue that the above tree is a balanced binary tree because after processing each node, we will discover that the value of k is not greater than 1.       

The leaf nodes in the aforementioned tree are n6, n4, and n3, with n6 being the node that is furthest from the root node. The height of the aforementioned tree is three since there are three edges between the root node and the leaf node. When we take node n1 to be the root node, nodes n2, n4, n5, and n6 are found in the left subtree, whereas node n3 is found in the subtree. N2 is a root node and N4 and N6 are leaf nodes in the left subtree. Because n6 has two edges and is the node that is furthest from its root node among nodes n4 and n6, the height of the left subtree is 2.

There are no offspring on the left or right of the right subtree, hence its height is zero. Since the right subtree is zero in height and the left subtree is two heights, the height difference between the two subtrees is two. The definition states that there cannot be a height difference of more than one between the left and right subtrees. The above binary tree is an unbalanced binary search tree since the difference in this instance is 2, which is more than 1.