Set Matrix Zeros in Java
In coding round interviews, it is frequently asked as the most significant challenge.
an m*n matrix is provided. Set the entire column and row of the matrix to 0 if any element is 0. Keep in mind that the operation shouldn't use any more arrays.
Think of the following matrix as an example.
Input:
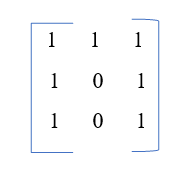
Output

The second row, as well as the second column elements in the array above both, have the value 0. In light of this, we will set each element in the second column and row to 0.
Java code to set matrix zeros
Different Approaches
The following three approaches can be used to fix the issue:
- Brute force approach
Using stacked loops and auxiliary space, the brute force method.
- Hash table approach
keeping an eye on the state of the hash table's rows and columns.
- In-place hashing approach
Using In-Place Hashing: Store the hash in the matrix's top row and bottom column.
Brute Force Approach
The practice of setting matrix zeros is foolish. In this method, we iterate through the matrix, updating each row and column to 0 for every 0. The method is quite simple, however, it could result in an incorrect answer.
Steps
Step1: Makean (n x m)-dimensional array response and initialize each element to 1.
Step 2: If the current row includes an element equal to 0, proceed row-by-row across the matrix array as well as set its current row as 0 in the response array.
Step 3: If the present column contains an element equal to 0, move column-by-column across the matrix array and set the current column as 0 in the response array.
Step 4: Now, as you traverse the response array if the element you are on is 0, set it to 0 in a matrix array.
Step 5: Return the Matrix array.
Pseudocode
void setMatrixZero(int a[][], int m, int n)
{
int temp[m][n]
for (i = 0 to m-1)
for (j = 0 to n-1)
temp[i][j] = 1
for(i = 0 to m - 1)
{
for (j = 0 to n - 1)
{
if (a[i][j] == 0)
{
for (k = 0 to m - 1)
temp[k][j] = 0
for (k = 0 to n - 1)
temp[i][k] = 0
}
}
}
for (i = 0 to M-1)
for (j = 0 to N-1)
arr[i][j] = temp[i][j]
}
In the method described above, we have explored every row and column of the appropriate matrix cell. The aforementioned method has an O(n*m(n+m)) time complexity and an O(n*m) space complexity for recording the primary matrix.
But it's our job to carry out the same action without taking up extra room. The same is shown in the approaches that follow.
Example program
public class SetMatrixZeroes {
public static void setZeroes(int[][] matrix, int n, int m) {
int ans[][] = new int[n][m];
for (int i = 0; i< n; i++) {
for (int j = 0; j < m; j++) {
ans[i][j] = 1;
}
}
for (int i = 0; i< n; i++) {
for (int j = 0; j < m; j++) {
if (matrix[i][j] == 0) {
for (int k = 0; k < m; k++) {
ans[i][k] = 0;
}
break;
}
}
}
for (int j = 0; j < m; j++) {
for (int i = 0; i< n; i++) {
if (matrix[i][j] == 0) {
for (int k = 0; k < n; k++) {
ans[k][j] = 0;
}
}
}
}
for (int i = 0; i< n; i++) {
for (int j = 0; j < m; j++) {
if (ans[i][j] == 0) {
matrix[i][j] = 0;
}
}
}
}
public static void main(String[] args) {
int[][] matrix = new int[][] {{1, 1, 1}, {1, 0, 1}, {1, 1, 1}};
int n = matrix.length;
int m = matrix[0].length;
setZeroes(matrix, n, m);
for (int i = 0; i< n; i++) {
for (int j = 0; j < m; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
matrix = new int[][] {{0, 1, 2, 0}, {3, 4, 5, 2}, {1, 3, 1, 5}};
n = matrix.length;
m = matrix[0].length;
setZeroes(matrix, n, m);
for (int i = 0; i< n; i++) {
for (int j = 0; j < m; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
}
The output of the above program
1 0 1
0 0 0
1 0 1
0 0 0 0
0 4 5 0 0 3 1 0
Hash Table Approach
We will employ a hash table to perform the same action. We will first create a HashTable and set all of the matrix's rows and columns to false. When the value of a row or column was changed from false to true, its value was set to 0.
Steps
Step 1: Make two HashTables with M and N-sized columns and rows, respectively.
Step 2: Set all of the row[] and col[] values to false at the beginning.
Step 3: Now, iterate through the matrix, setting row[i] and col[j] to true for each time a[i][j] == 0.
Step 4: Once step 3 is complete, traverse over matrix a once again and change any value a[i][j] to 0 if row[i] and otherwise col[j] are true.
Pseudocode
void setMatrixZeros(int a[][], int m, int n)
{
bool row[m], col[n]
for(i = 0 to m-1)
row[i] = false
for(j = 0 to n-1)
col[j] = false
for(i = 0 to m-1)
{
for(j = 0 to n-1)
{
if(a[i][j] == 0)
{
row[i] = true
col[j] = true
}
}
}
for(i = 0 to m-1)
{
for(j = 0 to n-1)
{
if(row[i] == true or col[j] == true)
arr[i][j] = 0
}
}
}
The time complexity of the aforementioned method is O(n*m). Due to the time required to create two hash tables, fill them with values, traverse them, and update them (O(n*m)). Because of this, the temporal complexity is O(n*m).The complexity of the storage space is increased by the usage of two hash tables.i.e, O(n+m)
The aforementioned strategy is likewise not optimal. The in-place hashing can be used to provide the optimal answer.
In-place Hashing Approach
This method involves storing row and column hashes in the matrix component. The matrix's initial row and column can be used to hold, respectively, the position of the matrix's rows and columns. The initial row and column status, which can be managed using two variables, will provide a challenge.
Steps
Step 1: First, define two variables. To store the state of the first column and first row, use the row, and the first column. Make them false.
Step 2: Use this row and column to store the row's and column's status in a hash.
Step 3: As you iterate through the matrix, set a[i][0] = 0 and col[0][j] = 0 for each time a[i][j] == 0.
Step 4: If a[i][0] = true for a[i][j] or a[0][i] = true for a[i][i], then set all of the matrix's values to 0 except for the first row and column.
Step 5: Update the first row's and first column's values last.
Pseudocode
void setMatrixZeros(int a[][], int m, int n)
{
for(j = 0 to n-1)
if(a[0][j] == 0)
firstRow = true
for(i = 0 to M-1)
if(a[i][0] == 0)
firstCol = true
for(i = 0 to m-1)
{
for(j = 0 to n-1)
{
if(a[i][j] == 0)
{
a[i][0] = 0
a[0][j] = 0
}
}
}
for (i = 1 to m-1)
{
for (j = 1 to N-1)
{
if(a[0][j] == 0 || a[i][0] == 0)
a[i][j] = 0
}
}
if(firstRow == true)
{
for( i = 0 to n-1 )
a[0][i] = 0
}
if(firstCol == true)
{
for(i = 0 to m-1)
a[i][0] = 0
}
}
The above method has an O(m*n) time complexity because we traversed the first row and the first column, updating the matrix, and finally modifying the first row as well as the first column, which takes O(m) + O(n) time (n). As a result, O(m*n) is the time complexity. Since we did not employ an auxiliary array, the space complexity is O. (1).
Example program of the set matrix to zeros in java
public class SetMatrixZeros
{
private static void setZeros(int[][] matrix, int n, int m)
{
int ans[][] = new int[n][m];
for (int i = 0; i< n; i++)
{
for (int j = 0; j < m; j++)
{
ans[i][j] = 1;
}
}
for (int i = 0; i< n; i++)
{
for (int j = 0; j < m; j++)
{
if (matrix[i][j] == 0)
{
for (int k = 0; k < m; k++)
{
answer[i][k] = 0;
}
break;
}
}
}
for (int j = 0; j < m; j++)
{
for (int i = 0; i< n; i++)
{
if (matrix[i][j] == 0)
{
for (int k = 0; k < n; k++)
{
ans[k][j] = 0;
}
}
}
}
for (int i = 0; i< n; i++)
{
for (int j = 0; j < m; j++)
{
if (ans[i][j] == 0)
{
matrix[i][j] = 0;
}
}
}
}
public static void main(String args[])
{
int[][] matrix = new int[][]
int n = matrix.length;
int m = matrix[0].length;
setZeros(matrix, n, m);
for (int i = 0; i< n; i++)
{
for (int j = 0; j < m; j++)
{
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
}
The output of the above program
0 0 0 0
0 8 0 0
0 0 0 0