Fibodiv Number in Java
Before understanding the concept of the fibodiv number, one should realize what the Fibonacci number is.
What are Fibonacci Numbers?
The Fibonacci sequence of whole numbers is composed of the numbers 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,... Every number is the sum of the two numbers that came before it. These intriguing details concern the Fibonacci numbers:
- This series is infinite and is known as the Fibonacci series.
- The Fibonacci series or sequence has an Fn symbol for each number.
If we consider f1 and f2 to be the first two terms of a Fibonacci series, then one of the terms of the series is the number N itself. This number N can be divided into parts f1 and f2. Let's use some examples to help us understand it.
Example 1
N = 14
In this instance, the number 14 can be divided into the digits 1 and 4. The Fibonacci series' first two terms are therefore f1 = 1 and f2 = 4. As a result, the series
1, 4, 5 (1 + 4), 9 (4 + 5), 14 (5 + 9), 23 (9 + 14)
The number 14 is present in the series above. 14 is, therefore, a fibodiv number.
Example 2
N = 15
In this instance, the number 15 can be divided into the digits 1 and 5. The Fibonacci series' first two terms are therefore f1 = 1 and f2 = 5. As a result, the series
1, 5, 6 (1 + 5), 11 (5 + 6), 17 (6 + 11), 28 (11 + 17)
The number 15 is not present in the series above. 15 is, therefore, not a fibodiv number.
Example 3
N = 1292
In this case, 1292 can be divided into 129 and 2. Therefore, f1 = 129 and f2 = 2 are the first two terms of the Fibonacci series. The series then reads as follows:
129, 2, 131 (129 + 2), 133 (2 + 131), 264 (131 + 133), 397 (133 + 264), 661 (264 + 397), 1058 (397 + 661), and 1719.
N = 1292
In this case, 1292 can be divided into 129 and 2. Therefore, f1 = 129 and f2 = 2 are the first two terms of the Fibonacci series. The series then reads as follows:
129, 2, 131 (129 + 2), 133 (2 + 131), 264 (131 + 133), 397 (133 + 264), 661 (264 + 397), 1058 (397 + 661), and 1719.
The number 1291 does not appear in the above-said series. We now divide 1292 into two additional parts, 12 and 92. Therefore, f1 = 12 and f2 = 92 are the first two terms in the Fibonacci series. As a result, the series is composed of the numbers 12, 92, 104 (12 + 92), 196 (92 + 104), 300 (104 + 196), 496 (196 + 300), 796 (300 + 496), and 1292 (496 + 796). 1292 is a Fibodiv number as a result.
Algorithm
Step 1: Pick the number N.
Step 2: To get the number N, divide the number into two parts, f1 and f2, respectively.
For instance, 59 can be divided into 5 and 9 (f1 and f2, respectively). The result of appending 9 and 5 is the number 59.
Step 3: Consider the terms f1 and f2 to be the first two in a Fibonacci-like series.
Step 4: Update f1 and f2 after computing the following term (let's say f3) by adding f1 and f2. f1 becomes f2, and f2 becomes f3, respectively.
Step 5: Continue to step 4 until the next term, f3 exceeds N, or f3 equals N.
Step 6: If f3 = N, then N is a Fibodiv number; otherwise, repeat step 2 for various f1 and f2 values (see example 3). N is not a Fibodiv number if it is impossible to divide it by the distinct values of f1 and f2.
Java Program for Fibodiv Number
Let's examine how the above algorithm is used to implement the tug-of-war problem.
Using Iteration
Filename: Example1.java
public class Example1
{ //Example1 is the class here
//a method that determines the value of b^e
public int pow(int b, int e)
{
int a = 1 ;
while(true)
{
if(e % 2 == 1)
{
e = e – 1 ;
a = a * b ;
}
// terminating condition
if(e == 0)
{
return a ;
}
b = b * b ;
e = e / 2 ;
}
}
//a method to determine whether or not
// n is a Fibodiv number
public boolean isFibodiv(int n)
{
int div = 10 ;
//A fibodiv number cannot be a single-digit number.
if(n / div == 0)
{
return false ;
}
int cn = 1 ;
//The variable v will divide the number n into parts.
int v = pow(div, cn) ;
//If (n / v) == 0, then further partitioning of
//n is impossible.
while((n / v) != 0)
{
// f1 represents the first part of the number n.
// The second part of the number n is f2.
//The first and second numbers in the fibonacci-like
//series are also designated as f1 and f2, respectively.
int f1 = n / v ;
int f2 = n % v ;
// calculating the next term in the Fibonacci-like series
int f3 = f1 + f2 ;
//There is no need to continue processing if f3 is greater than n.
while(f3 <= n)
{
//n is the Fibodiv number if f3 == n.
if(f3 == n)
{
return true ;
}
// updating f1 and f2
f1 = f2 ;
f2 = f3 ;
// computing the next term
f3 = f1 + f2 ;
}
// increasing the value of cn by 1
cn = cn + 1 ;
//By changing the value of v, different values of f1 and f2
//will result in the following iteration.
v = pow(div, cn) ;
}
// reaching here means
// n is not a Fibodiv number
// Hence, returning false
return false ;
}
// main method
public static void main(String argvs[])
{
// creating an object of the class Example1
Example1 obj = new Example1() ;
// a loop for finding the Fibodiv numbers lying
// between 1 to 100
for(int i = 1; i <= 100 ; i++)
{
if(obj.isFibodiv(i))
{
System.out.println(i + " is a Fibodiv number.") ;
}
}
}
}
Output
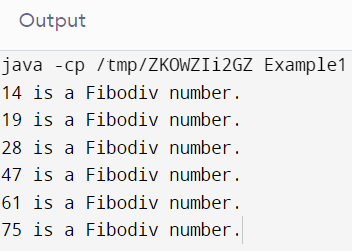
In the above-displayed output, the fibodiv numbers are 14, 19, 28, 47, 61, and 75.
Using Recursion
Filename: Example2.java
public class Example2
{ //Example2 is the class here
// A method that checks whether n
// is a Fibodiv number or not
public boolean isFibodiv(int n, int div)
{
// a single digit
// number cannot be
// a Fibodiv number
// If div is greater
// than n then also
// the number cannot be
// divided
if(n / div == 0)
{
return false ;
}
// f1 is the first part of the number n
// f2 is the second part of the number n
// f1 and f2 also serve as the first and second number
// of the Fibonacci-like series, respectively
int f1 = n / div ;
int f2 = n % div ;
// computing the next term of the Fibonacci-like series
int f3 = f1 + f2 ;
// if f3 is greater than n
// then there is no need to process further
while(f3 <= n)
{
// if f3 == n
// Then n is the Fibodiv number
if(f3 == n)
{
return true ;
}
// updating f1 and f2
f1 = f2 ;
f2 = f3 ;
// computing the next term
f3 = f1 + f2 ;
}
// recursively partitioning the number
// from different positions, which
// leads to the different values of f1 and f2
return isFibodiv(n, div * 10) ;
}
// main method
public static void main(String argvs[])
{
// creating an object of the class Example2
Example2 obj = new Example2() ; //obj is created
// a loop for finding the Fibodiv numbers lying
// between 1 to 100
for(int i = 1; i <= 100 ; i++)
{
if(obj.isFibodiv(i, 10))
{
System.out.println(i + " is a Fibodiv number.") ;
}
}
}
}Output
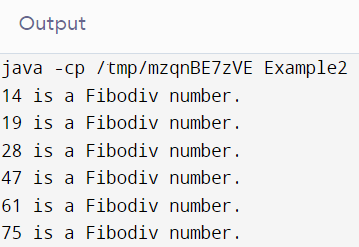
In the above-displayed output, the fibodiv numbers are 14, 19, 28, 47, 61, and 75.