Missing Number in an Arithmetic Progression in Java

Given an array that shows the elements of an orderly arithmetic progression. Find the missing number to complete the succession of elements.

Example: 

Input: a [ ] = {2 , 4 , 6 ,10 , 12 , 14 }

Output: 8

Explanation

The above sequence is in Arithmetic Progression with difference 2. We can find the missing element by traversing through the sequence. 8 is missing in the above sequence.

Method 1:Using Mathematical Formula

Finding the missing number by linearly navigating the array is a Simple Solution. This solution's time complexity is O (n).

According to mathematical formulas, the sum of the n elements in an AP is equal to (n/2)(a+l).

The number of components is n, and the first and last elements are a and l, respectively.

If we use this formula and maintain the results in a variable called s, we can add up all the components and keep the result in total. By using s-sum, we will find the missing number.

Program to find the missing number in given sequence in Java

MissingNumberAP.java

import java . io . * ;
class MissingNumberAP {
static int Missing ( int[] arr , int n )
{
int first , last , s , i , sum = 0 , number ;
first = arr [ 0 ] ;
last = arr [ n - 1 ] ;
if ( ( first + last ) % 2 == 0 ) 
{
s = ( first + last ) / 2 ;
s = s * ( n + 1 ) ;
}
else {
s = ( n + 1 ) / 2 ;
s = ( first + last ) * s ;
}
for ( i = 0 ; i <= n - 1 ; i++ ) {
sum = sum + arr [ i ] ;
}
number = s – sum ;
return number ;
}
public static void main ( String [ ] args  )
{
int  a[] = { 2 , 4 , 6 , 10 , 12 , 14 } ;
int l = a . length ;
System . out . println(" Missing element in the sequence is "+ Missing ( a, l ) ) ;
}
}

Output:

Let’s see another approach for the same.

Binary Search can also be used to address this issue in O(Logn) time. The goal is to reach the middle component. In order to determine whether the missing piece is between middle and middle+1, determine whether the difference between middle and next to middle equals diff or not. The missing element is in the right half if the middle element is equal to the n/2th term in the Arithmetic Series. Other component is in the left half.

MissingNumberAP2.java

import java.io.*; 
class MissingNumberAP2
{
static int findMissing(int arr[], int l, int h, int diff)
{
if ( h <= l )
return Integer . MAX_VALUE ;
int mid = l + ( h - l ) / 2 ;
if ( arr [ mid + 1] - arr [ mid ] != diff )
return ( arr [ mid ] + diff ) ;
if ( mid > 0 && arr [ mid ] - arr [ mid - 1 ] != diff )
return ( arr [ mid - 1 ] + diff ) ;
if ( arr [ mid ] == arr [ 0 ] + mid * diff )
return findMissing ( arr , mid + 1 , h , diff ) ;
return findMissing ( arr , l , mid - 1 , diff ) ;
}
static int Missing ( int a [ ] , int n)
{
int d = (a [ n - 1 ] - a [ 0 ] ) / n ;
return findMissing(a, 0, n - 1, d ) ;
}
public static void main (String[] args)
{
int a [ ] = {2 , 4 , 6 , 8 , 12 , 14 } ;
int l = a . length ;
System . out . println ("The missing element is "+ Missing ( a, l ) ) ;
}
}

Output:

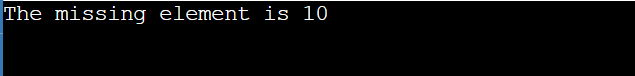
Let’s see the efficient approach.

The goal is to reach the central component. If the middle element's index is equal to 1, the missing element is located in the right half; otherwise, it is located in the left half. The missing element will be located between high and low after breaking free of the binary search cycle. By combining a common difference with an element at index high or a common difference with an element at index low, we can identify the missing element.

MissingNumberAP3.java

import java . io . * ;
class MissingNumberAP3
{
// static method declaration
static int Missing(int arr [ ] , int l ,int h , int diff )
{
int mid ;
while ( l <= h )
{
mid = ( l + h ) / 2 ;
if ((arr[mid] - arr[0]) / diff == mid)
l = mid + 1;
else
h = mid - 1;
}
return arr[h] + diff;
}
static int Missing(int a [ ] , int n)
{

int d = (a [n - 1] - a [ 0 ] ) / n ;


return Missing ( a , 0 , n - 1 , d ) ;
}


// Main method where execution of the program starts
public static void main (String[] args)
{
int a [ ] = { 2 , 4 , 6 , 10 , 12 , 14 } ;
int l = a . length;
System . out . println ( " The missing element is " + Missing ( a , l ) ) ;
}
}

Output