Figurate Number in Java

There have been several uses for figurate or figural numerals throughout history. A number that may be expressed by regular, distinct geometric shapes with spaced evenly points is referred to as a figurate number. If the arrangement of the points forms a normal polygon, regular polyhedron, or regular polytope, then the integer may be a hexagonal, polyhedral, or polytopic number.

Frugal Number

When neat lines connect n points in general location on a circle, the number of triangles (all whose vertices fall inside the circle) are created.

Figured number, sometimes called a figural identifier. The number is a polygonal integer if the configuration creates an irregular polygon. It is an integer that may be represented by an even series of orderly geometrical arrangements of points. The figurate numerals are shown below, along with their order.

1.Triangular Number : 1, 3, 6, 10, 15, 21, 28……

2. Square Number :1, 4, 9, 16, 25, 36, 49……

3. Pentagonal Number : 1, 5, 12, 22, 35, 51, 70….

Properties

The expansion of (a1 + a2 + a3 + a4 + a5 + a6 + a7)^n has the number of words a(n). This sequence only contains one prime number: 7. Triangle numbers in six dimensions, sixth part sum of factorial transform of [1, 0, 0, 0,...].

fallacy(n, 6)/6 = a(n). is also a rank six, dimension n >= 1, non-symmetric tensor's overall number of separate components. Fallfac is the falling factorial in this case.

Whenever the primary key of the orbit was equal to 645120, the amount of Aut(Z7) orbits are provided as a function of the infinite norm n of the sample integer point on the surface of the orbit.

Formulas for Figuring Out Numbers

Calculation in general: x6/ (1-x) ^7

Equation for an exponential: exp(x)*x^6/720

Hypothesis:  a(n+3) = Sum{0 <= k, l, m <= n; k + l + m <= n} k*l*m

It contains some other formulas:

a(n) = (n^6 - 15*n^5 + 85*n^4 - 225*(n^3) + 274*(n^2) - 120*n)/720.

a(n) = 3*C(n+1, 6)

Example of Figurated Numbers

Consider the set Z = 1, 2, 3, 4, 5, 6 as an example. Applying the fifth property will help us determine the figurate number.

Make subsets of the provided set Z, each of which must contain five items.

We will obtain the below sets.

{1, 2, 3, 4, 5}, {1, 2, 3, 4, 6}, {1, 2, 3, 5, 6}..etc

Choose the lowest two integers from the abovementioned subsets, then sum them. Which is:

a(6) = (1+2) + (1+2) + (1+2) + (1+2) + (1+3) + (2+3) = 21

For some, we may apply the formula a(n) = 3*C(6+1,6). When we enter the values for n=6, we obtain:

a(6) = 21 = 3*C(6+1,6)

Let's use a different formula to determine whether 84 is a figurate number.

a(9) = (1, 3, 3, 1). (1, 6, 15, 20) = (1 + 18 + 45 + 20) = 84

Therefore, 84 is the ninth figurate number.

The initial figurate numerals are as follows: 0, 0, 0, 0, 0, 0, 0, 0, 1, 7, 28, 84, 210, 462, 924, 3003, 5005, 8008, 12376, 27132, 38760, 54264...

Using the Successive Difference Method

We may use consecutive differences to compute the figurate number. Let us discuss the below example of a Java-based Figurate Number.

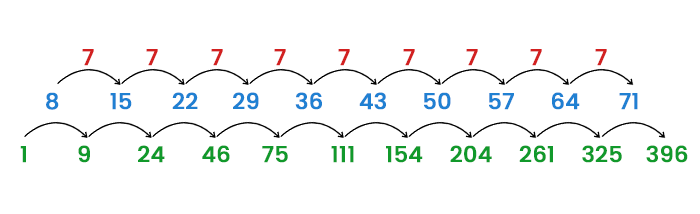
But the approach mentioned above isn't always useful.

Various types of Figurate Numbers:  

Figurate numbers in four dimensions (A002417) 

These formulas may be used to compute it:

A(n) = n*binomial(n+2, 3).

The sequence is A002417 from the OEIS.

The initial figurate numerals in four dimensions are:

1, 8, 30, 80, 175, 336, 588, 960.....

Properties:

1. A(n) is the number of color combinations in a 2 X 2 hexagonal array having (n+2) color combinations.
2. a(n) = (n^2)*(n+1)*(n+2)/6
3. The total of all integers that are not expressed as t*(n+1) + u*(n+2) for non-negative real integers t, u is equal to a(n).
4. The overall number of polygons (including squares) inside a stepping pyramid made up of n rows (or the base 2n-1) of squares is denoted by the symbol a(n).
5. The characteristics polynomials of the (n + 2) X (n + 2) matrix, which has 2s along the major vertical and 1s just about everywhere, has a(n) = -1 times the coefficient of x^3 of the matrix.
6. The convolutional array's n - th antidiagonal summation is denoted as a(n).

Moreover, the number of 3-cycles inside the (n+2)-triangular graph.

Regular Figurative Number (A090466)

The higher-order k-goal numbers have been sorted. Each integer would show up if the ranking 2 or the 2-goal numbers were included. The sequence is A090466 from the OEIS. It also goes by the name polygonal numbers.

For k = 1, 2, 3,..., there is the following words that are less than or equal to 10k: 3, 57, 622, 6357, 63889, 639946, 6402325, 64032121, 640349979, 6403587409, 64036148166, 640362343980, and so on.

There is at most one a(n) with p2 = a(n) + 1 for every squared of primes with p >= 5 (A001248). Therefore, just the subset P s(3) of rank 3 is required.

Java Program for figurate number

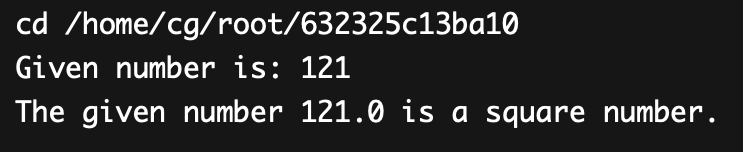
The below java program will describe the given number as a squared number:

FigurateExample.java

//This program is for checking whether the given number is figurate or not
//import section
import java.util.Scanner;    
public class FigurateExample  
{     
//method for checking whether the given number is the square number    
static boolean isSqureF(double number)      
{     
//finding the root of the given number    
double squareroot=Math.sqrt(number);     
//finding the floor of the square root value and then checking it with 0  
return ((squareroot - Math.floor(squareroot)) == 0);     
}     
//main method    
public static void main(String[] args)      
{     
System.out.print("Given number is: ");    
//creating an object for the scanner class
Scanner sc=new Scanner(System.in);    
//a number of double(data type) is read as an input from the user   
double number=sc.nextDouble();     
//   
if (isSqureF(number))     
System.out.print("The given number "+number+" is a square number.");     
else    
System.out.print("The given number "+number+" is not a square number.");     
}     
}

Output

Example2: NonaExample.java

//This program is for checking the given nonagonal number
//import section
import java.util.Scanner;  
public class NonaExample
{  
//function to check the Nonagonal number  
static int isNonagonal(int n)  
{  
//finding the n-th Nanagonal number
return n * (7 * n - 5) / 2;  
}  
//Main program 
public static void main(String args[])  
{  
Scanner sca = new Scanner(System.in);  
System.out.print("Please enter the position the needed: ");  
int n=sca.nextInt();  
System.out.println(n+" rd/th Nonagonal number is: "+isNonagonal(n));  
}  
}  

Output