Lazy Propagation in Segment Tree in Java

The topic of segment trees in Java is continued by the topic of sluggish propagation in segment trees. It is suggested that readers first read through the section tree topic. In a segment tree, lazy propagation means delaying the updating of certain values and changing them just when necessary.

Update operation

Let's think back to how a segment tree is updated.

• Start at the segment tree's base.
• Return if the current node's range does not include the input array's index.
• If not, update the current node and proceed to step 2 again for the current node's children.

The Lazy Propagation Scenario

Let's talk about a situation when the lazy propagation strategy would be appropriate.

Assume that the assignment is to add the number 6 to each of the input array's items from index 1 to 4. The update() method must be called for each item from index 1 to 4 to complete the operation. More time is spent as a result of these numerous calls. Here is where the update process becomes quick thanks to the lazy propagation strategy.

Be aware that the outcome of a search for just several indices is contained in a node of a segment tree. Furthermore, all of that node's descendants must be updated if the update operation's range overlaps with this node's range. In the picture above, for instance, the node with value 35 includes the total of elements at the indexes from 3 to 5. (See the above diagram). Modify that node and all of its descendants if the update's query falls within the range of 2 to 5.

We must upgrade the node with the number 35 via lazy propagation and postpone the changes of its successors by storing the updated information in different nodes known as sleepy nodes or values. To represent the lazy nodes, we make an array called lazy[]. The size of the array t[] in the following code is the same as that

of the array lazy[], which represents the segment tree.

The strategy is to initialize each element of the lazy[] array as 0. The segment tree node j has no changes pending, as shown by a value of 0 in the array lazy[j]. Any alternative value for lazy[j] (let's say it is v) signifies that the segment tree's node j must first be added to by an amount equal to v before any queries can be made.

How to Update a Node in a Segment Tree Using Lazy Propagation

//To reflect updates in the array elements in the segment tree

// Between x and y in the array.

updateRange (us, ue)

1) If there are any pending updates for any nodes in the current segment tree, then

complete that node's pending change first.

2) If the current node's range is entirely within the update query's range, update the current node first. Then, update any child nodes by setting their lazy values to true.

3) Use the same procedure as the last simple update if the current node's range overlaps the update range:

1. Recur for the left and right children.
2. Update the current node with the outcomes of the left and right calls.

The use of lazy propagation

LSTE1.java

public class LSTE1
{  
final int MAX_SIZE = 50;    
int s[] = new int[MAX_SIZE]; 
int l[] = new int[MAX_SIZE];
void updateRangeUtil(int currNode, int y, int z, int t, int f, int v)  
{
if (l[currNode] != 0)  
{ 
s[currNode] += (z - y + 1) * l[currNode];  
if (y != z)  
{  
l[2 * currNode + 1] += l[currNode];  
l[2 * currNode + 2] += l[currNode];  
}  
l[currNode] = 0;  
}
if (y > z || y > f || z < t)  
{  
return;  
}  
if (y >= t && z <= f)  
{ 
s[currNode] += (z - y + 1) * v; 
if (y != z)  
{  
l[2 * currNode + 1] += v;  
l[2 * currNode + 2] += v;  
}  
return;  
}  
int m = (y + z) / 2;  
updateRangeUtil(2 * currNode + 1, y, m, t, f, v);  
updateRangeUtil(2 * currNode + 2, m + 1, z, t, f, v);  
s[currNode] = s[2 * currNode + 1] + s[2 * currNode + 2];  
} 
void updateRange(int n, int y, int z, int v)   
{  
updateRangeUtil(0, 0, n - 1, y, z, v);  
}  
int getSumUtil(int y, int z, int t, int f, int si)  
{  
if (l[si] != 0)  
{  
s[si] += (z - y + 1) * l[si];  
if (y != z)  
{
l[2 * si + 1] += l[si];  
l[2 * si + 2] += l[si];  
}  
l[si] = 0;  
} 
if (y > z || y > f || z < t)  
{  
return 0;  
}  
if (y >= t && z <= f)  
{  
return s[si];  
}  
int m = (y + z) / 2;  
return getSumUtil(y, m, t, f, 2 * si + 1) +  
getSumUtil(m + 1, z, t, f, 2 * si + 2);  
}  
int getSum(int t, int y, int z)  
{ 
if (y < 0 || z > t - 1 || y > z)  
{  
System.out.println("Invalid input");  
return -1;  
}  
return getSumUtil(0, t - 1, y, z, 0);  
}  
void constructSTUtil(int b[], int y, int z, int si)  
{
if (y > z)  
{  
return;  
} 
if (y == z)  
{  
s[si] = b[y];  
return;  
}  
int m = (y + z) / 2;  
constructSTUtil(b, y, m, 2 * si + 1);  
constructSTUtil(b, m + 1, z, 2* si + 2);  
s[si] = s[2 * si + 1] + s[2 * si + 2];  
}  
void constructST(int b[], int t)  
{  
constructSTUtil(b, 0, t - 1, 0);  
}  
public static void main(String argvs[])  
{  
int b[] = {3, 5, 8, 11, 13, 14};  
int t = b.length;  
LSTE1 tObj = new LSTE1();  
tObj.constructST(b, t);  
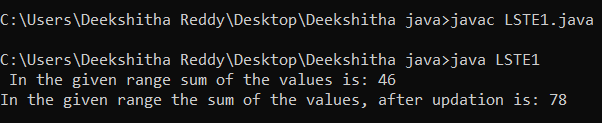
System.out.println(" In the given range sum of the values is: " +  
tObj.getSum(t, 2, 5));  
tObj.updateRange(t, 2, 10, 8);  
System.out.println("In the given range the sum of the values, after updation is: " +  
tObj.getSum(t, 2, 5));  
}  
}   

Output: