Minimum Number of Taps to Open to Water a Garden in Java
Problem Statement
The issue is that a gardener wants to water a (single-dimensional) garden using the fewest possible tap openings. The goal is to determine the minimum necessary taps to be open to water the entire garden adequately. If this is not possible, return -1.
The solution to the Problem
For the sake of simplicity, it is assumed that the garden is one-dimensional along an axis of length L, starting at point 0 and ending at point L. The points posArr = [0, 1, 2,..., T] in the garden are where T + 1 taps are located. For the jth tap, the range is defined as (j - rangeArr[j], j + rangeArr[j]). The range of a tap is specified in the array rangeArr[]. Keep in mind that if the entire garden cannot be watered, the console must display the proper message.
To help you understand, let's look at an example of it.
Example
Input
L = 5, rangeArr = [3,4,1,1,0,0]
Output
1
Explanation
The tap at point 0 can cover the interval [-3,3]
The tap at point 1 can cover the interval [-3,5]
The tap at point 2 can cover the interval [1,3]
The tap at point 3 can cover the interval [2,4]
The tap at point 4 can cover the interval [4,4]
The tap at point 5 can cover the interval [5,5]
Opening Only the second tap will water the whole garden [0,5]
Example with diagram
Input
L = 5, rangeArr = [1, 2, 3, 0, 4, 2]
Output
1
Explanation
- rangeArr[0] is 1 for the first location tap. The range is therefore [0 - 1, 0 + 1] = [-1, 1].
- rangeArr[1] is 2 for the second location tap. The range is therefore [1 - 2, 1 + 2] = [-1, 3].
- rangeArr[2] is 3 for the third location tap. It follows that the range is [2 - 3, 2 + 3] = [-1, 5].
- rangeArr[3] is 0 for the fourth location tap. The range is thus [3 - 0, 3 + 0] = [3, 3].
- rangeArr[4] is equal to 4 for the fifth location tap. It follows that the range is [4 - 4, 4 + 4] = [0, 8].
- rangeArr[5] is 2 for the sixth location tap. The available range is [5 - 2, 5 + 2] = [3, 7].
The same is depicted in the diagram below.
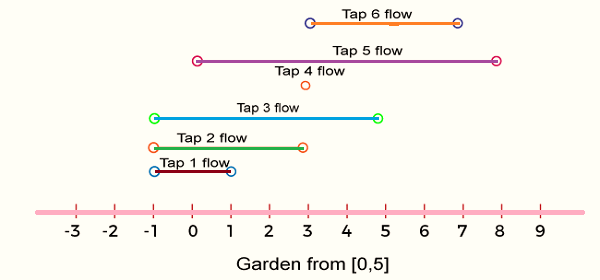
According to the diagram above, we can either open a tap in the third position rangeArr[2] or a tap in the fifth position range Arr[4]. This is because these taps can cover the entire length of the garden, ranging from 0 to 5. As a result, the answer is 1.
Algorithm
Step 1: To solve the problem, convert the array rangeArr[] into a list of intervals and sort them. Sorting should be done based on the starting point of the specified taps' range. Maintain the interval sorting in the array intervals[].
Step 2: Select an element from the array intervals[] (Picking should be done from left to right) and check the range's beginning and ending points (use the loop for picking the elements from the interval). There must be another tap within the range's finishing point; if it is not present, it is impossible to water the entire garden, so we can stop here to display an appropriate message. If the range is present, select the tap whose range is present and increment the tap count.
Step 3: Repeat step 2 for each tap until we locate a tap that can span the entire garden on its own or we have traversed all of the array intervals[]. Return the number of taps that are necessary (count of the tap).
The algorithm mentioned above is implemented as follows.
Filename: FillGardenWithWater.java
// significant import statements
import java.util.Comparator ;
import java.util.Arrays ;
public class FillGardenWithWater
{
public int minTapsFill(int rangeArr[], int size)
{
// Initializing the answer
int tapCount = 0 ;
int arrSize = rangeArr.length ;
// intervalFlow array that will include each tap's range
int intervalFlow[][] = new int[arrSize][2] ;
// The for loop is used to store the range.
for(int j = 0; j < arrSize; j++)
{
// identifying the starting and stopping places of the jth tap
int st ;
int ed ;
// Since the garden begins at 0
if(j - rangeArr[j] >= 0)
{
st = j - rangeArr[j] ;
}
else
{
st = 0 ;
}
ed = j + rangeArr[j] ;
//range is being added to the array intervalFlow
intervalFlow[j][0] = st ;
intervalFlow[j][1] = ed ;
}
// utilising the starting point to sort the intervalFlow.
// The tap with the earliest starting point will be selected first.
Arrays.sort(intervalFlow, new Comparator<int[]>()
{
@Override
//Compare values based on columns
public int compare(int[] e1, int[] e2)
{
if (e1[0] == e2[0])
{
return e1[1] - e2[1] ;
}
return e1[0] - e2[0] ;
}
}) ;
//the range that has been covered by the
//taps that have been walked through
int maximumRange = 0 ;
// the current tap's range
// that one is traversing right now
int nextMaximumRange = 0 ;
// for traversing the array's elements
// array intervalFlow[][]
int j = 0 ;
// Traversing the intervals
while(j < intervalFlow.length)
{
// the range goes out of the garden
if(maximumRange >= size)
{
return tapCount ;
}
// If in the range of the garden
//By opening the existing tap, you can extend the range.
if(intervalFlow[j][0] <= maximumRange)
{
while(j < intervalFlow.length && intervalFlow[j][0] <= maximumRange)
{
nextMaximumRange = Math.max(nextMaximumRange, intervalFlow[j][1]) ;
j = j + 1 ;
}
}
// dealing with the Case
else
{
return -1 ;
}
// Updating the maximum water flow
maximumRange = nextMaximumRange ;
// Activating the current tap
tapCount = tapCount + 1 ;
}
return tapCount ;
}
// main method
public static void main(String argvs[])
{
// making an object of the FillGardenWithWater class
FillGardenWithWater obj = new FillGardenWithWater() ;
// range of the garden is from 0 to 5
int L = 5 ;
// range of taps
// input 1
int rangeArr[] = {1, 2, 3, 0, 4, 2} ;
int answer = obj.minTapsFill(rangeArr, L) ;
if(answer == -1)
{
System.out.println("The taps cannot water the whole park.") ;
}
else
{
System.out.println("The minimum number of taps required to water the whole park is: " + answer) ;
}
// input 2
int rangeArr1[] = {3, 1, 1, 1, 0, 0} ;
answer = obj.minTapsFill(rangeArr1, L) ;
if(answer == -1)
{
System.out.println("The taps cannot water the whole park.") ;
}
else
{
System.out.println("The minimum number of taps required to water the whole park is: " + answer) ;
}
// input 3
int rangeArr2[] = {1, 1, 1, 1, 1, 1} ;
answer = obj.minTapsFill(rangeArr2, L) ;
if(answer == -1)
{
System.out.println("The taps cannot water the whole park.") ;
}
else
{
System.out.println("The minimum number of taps required to water the whole park is: " + answer) ;
}
}
}
Output
Complexity Analysis
We utilized loops and sorting in the preceding code. The loop yields O(n) in time, and the sorting is O(n * log(n)) in time. As a result, the program's total time complexity is O(n + n * log(n)), where n is the total number of taps located. Because the range is also stored in an array, the space complexity of the preceding program is O(n).
We can improve the preceding strategy by avoiding sorting. The following method illustrates this.
Optimized Method
Step 1: In this method, construct a jumpArr[] of size L + 1 to keep track of the maximum range that may be reached from the specified index (current index). To accomplish this, assign the value -1 to each entry of the array jumpArr[]. A value of -1 for any index indicates that it is impossible to attain that value (coordinate).
Step 2: Create a variable called tapCount and set it to 1.
Step 3: Find the range for each tap by iterating through the array rangesArr[]. The range can be calculated as:
start = maximum from (0, i - rangesArr[i])
end = minimum from (L, i + rangesArr[i])
Step 4: Update the jumpArr[] array as jumpArr[start] = maximum from (jumpArr[start], end). It is not possible to water the entire garden if jumpArr[0] = -1.
Step 5: Give the value jumpArr[0] to a variable called current. Take nxt and j as two additional variables as well. Both of them should be assigned the number 0.
While current < L, it indicates that the garden will receive a full watering at the last index L.
While j < current,
update nxt = maximum from (nxt and jumpArr[j])
increment j by 1.
It is impossible to move ahead if the nxt is the same as the current. As a result, it is only possible to water some of the ground.
current should be updated using nxt if it differs from current, and the tapCount should be updated by adding 1 to it.
Let's use a Java program to implement the above technique.
FileName: FillGardenWithWater1.java
// significant import statement
import java.util.Arrays ;
public class FillGardenWithWater1
{
public int minTapsFill(int rangeArr[], int L)
{
// Initializing the answer
int tapCount = 1 ;
int arrSize = rangeArr.length ;
// Initializing the array of the size L + 1 with all the values as -1
int jumpArr[] = new int[L + 1];
Arrays.fill(jumpArr, -1) ;
// Traversing the array rangeArr[]
for(int j = 0; j <= L; j++)
{
//Updating the jumpArr[] array with
//the maximum flow possible
// calculating the range for each tap
// The start of the range is at st
//As the value that goes beyond
//The number 0 serves no use. As a result,
//we check with a value of 0.
int st = Math.max(0, j - rangeArr[j]) ;
// The range's termination point is ed.
//As the value that goes beyond
// L has no practical use. As a result,
//we verify using the value L.
int ed = Math.min(L, j + rangeArr[j]) ;
jumpArr[st] = Math.max(jumpArr[st], ed) ;
}
// Indicating that no tap is able to water the
// first coordinate of the garden
if(jumpArr[0] == -1)
{
return -1 ;
}
//current suggests that in order to achieve
//the maximum flow, the tap must be opened.
int current = jumpArr[0] ;
int j = 0 ;
int nxt = 0 ;
// for traversing the garden completely
while (current < L)
{
//Finding the next tap to open in order to water
//the largest possible area of the garden,
//it is done to limit the number of taps
//to a minimum(count of taps to a minimum).
while (j <= current)
{
nxt = Math.max(nxt, jumpArr[j]) ;
j = j + 1 ;
}
//it denotes that advancement is not feasible.
//Consequently, it is impossible
//to water the entire garden.
if (nxt == current)
{
return -1 ;
}
// Using the current tap
current = nxt ;
// updating the answer
tapCount = tapCount + 1 ;
}
return tapCount ;
}
// main method
public static void main(String argvs[])
{
FillGardenWithWater1 obj = new FillGardenWithWater1() ;
// range of the garden is from 0 to 5
int L = 5 ;
// range of taps
// input 1
int rangeArr[] = {1, 2, 3, 0, 4, 2} ;
int answer = obj.minTapsFill(rangeArr, L) ;
if(answer == -1)
{
System.out.println("The taps cannot water the whole park.") ;
}
else
{
System.out.println("The minimum number of taps required to water the whole park is: " + answer) ;
}
// input 2
int rangeArr1[] = {3, 1, 1, 1, 0, 0} ;
answer = obj.minTapsFill(rangeArr1, L) ;
if(answer == -1)
{
System.out.println("The taps cannot water the whole park.") ;
}
else
{
System.out.println("The minimum number of taps required to water the whole park is: " + answer) ;
}
// input 3
int rangeArr2[] = {1, 1, 1, 1, 1, 1} ;
answer = obj.minTapsFill(rangeArr2, L) ;
if(answer == -1)
{
System.out.println("The taps cannot water the whole park.") ;
}
else
{
System.out.println("The minimum number of taps required to water the whole park is: " + answer) ;
}
}
}
Output
Complexity Analysis
We employed the while loop's nesting feature in the program mentioned above. The elements of the array jumpArr[] are still only iterated through once, though. It results from both while loops working in the same direction, which causes the program's time complexity to be O (N). Additionally, we added an auxiliary array to keep track of the maximum range, making the program's space complexity O(N), where N is the total number of taps in the garden.