Java Boyer Moore
A string searching or matching technique called the Boyer-Moore algorithm was created in 1977 by Robert S. Boyer and J. Strother Moore. It is the most popular and effective string-matching algorithm. Compared to the brute-force algorithm, it is substantially faster. The Boyer-Moore algorithm, its features, and its application in a Java program will all be covered in this article. It has a temporal complexity of O(nm+s). In most applications, the Boyer-Moore algorithm is the most efficient string-matching algorithm. In text editors, the «search» and «substitute» commands frequently use a simplified version of the algorithm or the entire algorithm.
Worst-case scenario
T=ssssssss……sssssss………ssssssss
P=psssssssss
The above sequence can be found in images and DNA sequences.
Characteristics of the Boyer Moore Algorithm
- From right to left, it compares each character;
- O(m+) time and space complexity characterize the pre-processing stage.
- The searching step has an O(mn) complexity.
- In the worst scenario, it compares 3n text characters when looking for a non-periodic pattern.
- The complexity with the best performance is O(n/m).
The algorithm is based on the two heuristics listed below:
- Character-Jump Heuristics
- Looking-Glass Heuristics
Let's examine how the Boyer-Moore algorithm works.
The Boyer-Moore algorithm's operation
The method begins tracing characters from the pattern's rightmost character and advances leftward. It employs two pre-computed functions that shift the characters to the right and left, respectively, in the event of any mismatch and complete pattern matching. The good-suffix shift (also known as the matching shift) and the bad-character shift (or occurrence shift) are the names of these two pre-computed shift functions.
Note: Characters should be compared in a right-to-left sequence and aligned left to right to match the pattern.
Bad Character Shift
Skip alignment when there is a mismatch up until one of the following situations does not exist:
- Mismatch turns into a match
- P avoids mismatching characters
Take the text (T) and pattern (P) shown below as examples.
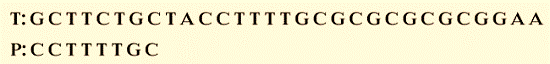
Start comparing the pattern now.
Step 1: First, align characters from left to right and compare them from right to left.
We can see that the last three characters of P correspond to those in T. T, the fourth character, is mismatched. As per the above guideline, skip alignment until a mismatch becomes a match. The seventh character (C) in P matched with C in T.
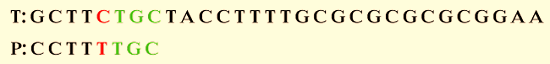
The above-displayed image shows the partial match.
Step 2: Move three characters to the right to match the pattern.
Compare the characters once more, this time from right to left, after moving. It matches the first character. We see that the character A is absent from the position to the left of P. P then shifts to the past mismatch character (A) in T in this instance.
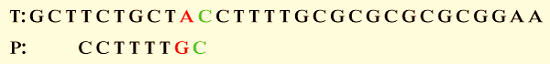
The above-displayed image shows the procedure through which P and T attain matches.
Step 3: If P is moved past the mismatched character, we get,
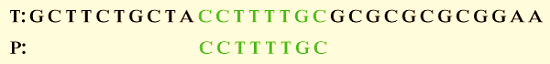
From the above-displayed image, the pattern is matched. The sequence “CCTTTTGC” matches in both the T and P.
Note: The bad-character shift may not be good. Given that the Boyer-Moore method applies the maximum (skip characters) between the good-suffix shift and bad-character shift, it is appropriate to shift characters in this manner.
Good-Suffix Shift
Let's say that an inner loop matches the substring t. If so, skip characters up until:
- No mismatches exist between P and t.
- P moves past t.
Consider the following pattern as an example.

Step 1: Go from right to left and compare the characters. We can see that the last three characters of P correspond to characters in T denoted by t.

The above-displayed image shows the partial match.
Step 2: Continue until there is no match between P and t. The first four characters (from left to right) of P (C T T A C) correspond to the last five characters in t.
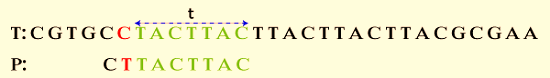
The above-displayed image shows the procedure through which P and t attain no matches.
Step 3: To get the match, skip three alignments. As a result, we get the match.

The above-displayed image shows the match. The sequence “CTTACTTAC” matches in both the T and P.
The two-shift functions described above can be defined as follows:
The good-suffix shift function is stored in a table of size m+1 called “bmGs”. The table “bmGs” is computed using a table “suff” defined as follows:
for 1 ? i < m, suff[i]=max{k : x[i-k+1 .. i]=x[m-k .. m-1]}
The bad-character shift function is stored in a table bmBc of size s. For c in ∑:
bmBc[c] = min{i : 1 ? i <m-1 and x[m-1-i]=c} if c occurs in x, m otherwise.
Pattern Matching Example Using Boyer Moore
Think about the following pattern.
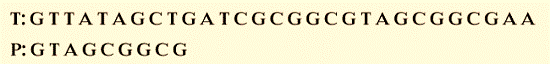
Let's begin matching.
Step 1: Characters should be compared from right to left. The first character is mismatched, as G does not match with T.
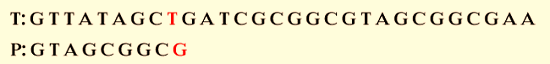
Step 2: Skip the following few characters until we find a match. After six characters, a match is made. The good suffix shift rule will not be applicable in this case.
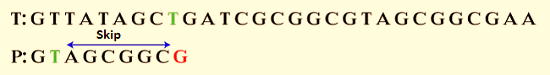
P moves past mismatch character (i.e. G), according to bad character shift.
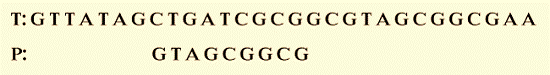
Step 3: Compare characters once more from right to left. We can observe that P's first three characters match (t) with T, but its fourth character does not.
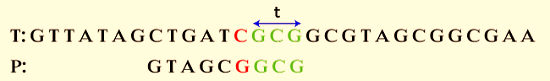
Both the bad and good character suffix can be used in this situation. When the bad character suffix is used, only one character is skipped. The good character suffix ignores two alignments when used. Therefore, since the algorithm says to skip additional alignments, we will use the good character suffix. Consequently, we omit two alignments.
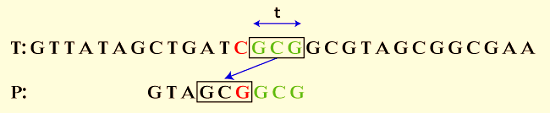
Three characters of alignment are changed, and the result is:
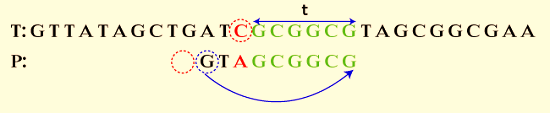
Here, we can see that C is missing from P's area to the left. Good character alignments skip seven alignments, while bad character alignments skip two alignments.
Step 4: We can observe that the string is matched after changing a few characters.
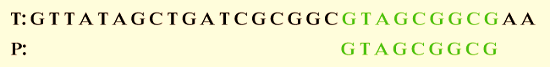
We skipped 15 alignments in the earlier pattern, and 11 T characters were ignored.
Boyer Moore Pre-processing Phases
The following definition applies to calculated skips for the patterns T: A A T C A A T A G C and P: T C G C. The bad character shift function was employed in the above pattern.
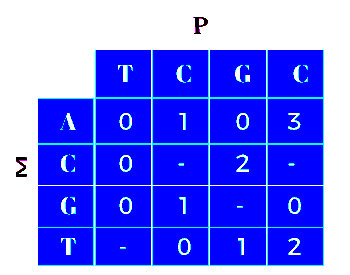
The above table (characters) shows the number of skip alignments.
Pseudo Code for the Boyer Moore Algorithm
BoyerMooreMatch(H, T, ?)
K<- lastOccurenceFunction(T, ?)
i <- m-1
j <- m-1
repeat
if H[i]=T[j]
if j=0
return i {match at i}
else
i <- i-1
j <- j-1
else
{character-jump}
K<-K[H[i]]
i <- i +m -min(j, 1+ l)
j <- m-1
until i>n-1
return-1 {no match}
Java Program for Pattern Searching
Let's look at the pattern-finding Java program. The brute-force string searching algorithm is implemented in the following program.
File name: PatternSearchingExample.java
import java.util.HashMap;
import java.util.Map;
public class PatternSearchingExample
{
/**
* @example text -- trace the text to see if it contains pattern
* @example pattern -- look for this text inside the text parameter
* @return -- return index of the first match or -1 if not found
*/
public static int findBruteForce(char[] text, char[] pattern)
{
System.out.println("Brute force looking for " + String.valueOf(pattern) + " in " + String.valueOf(text)) ;
int n = text.length ;
int m = pattern.length ;
//checks if the string is empty
if (m == 0) return 0 ;
//brute force it -- loop over all characters in text O(n)
for (int i=0;i<=n-m;i++)
{ //index into the text
//loop over all characters in pattern while characters match O(m)
//index into the pattern
int k = 0 ;
while (k<m && text[i+k] == pattern[k])
{
k++ ;
}
//if at the end of the pattern, then found match starting at index i in text
if (k==m)
{
System.out.println("\tFound match in the given text at index " + i) ;
return i ;
}
}
//if a match is not found
System.out.println("\tNo match found in the given text.") ;
return -1 ;
}
/**
* @example text -- search this text to see if it contains pattern
* @example pattern -- look for this text inside the text parameter
* @return -- return index of the first match or -1 if not found
*/
public static int findBoyerMoore(char[] text, char[] pattern)
{
System.out.println("Boyer-Moore looking for " + String.valueOf(pattern) + " in " + String.valueOf(text)) ; //valueOf method is used
int n = text.length ; // n stores length of the text
int m = pattern.length ;
// Test for empty string
if (m == 0) return 0 ;
// Initialization, create Map of last position of each character = O(n)
Map<Character, Integer> last = new HashMap<>() ; //Map
for (int i = 0; i < n; i++)
{
// set all chars, by default, to -1
last.put(text[i], -1) ;
}
for (int i = 0; i < m; i++)
{
// update last seen positions
last.put(pattern[i], i) ;
}
//Start with the end of the pattern aligned at index m-1 in the text.
//index into the text
int i = m - 1 ;
// index into the pattern
int k = m - 1 ;
while (i < n)
{
if (text[i] == pattern[k])
{
// match! return i if complete match; otherwise, keep checking
if (k == 0)
{
System.out.println("\tFound match in the given text at index " + i) ;
return i ;
}
i = i - 1 ;
k--;
}
else
{ // jump step + restart at end of pattern
//iterate over the text
i += m - Math.min(k, 1 + last.get(text[i])) ;
//move to the end of the pattern
k = m - 1 ;
}
}
System.out.println("\tNo match found in the given text.") ;
// prints as not found
return -1 ;
}
public static void main(String args[])
{
char[] text = "abcfefabddef".toCharArray() ; //string to character array
char[] pattern = "abddef".toCharArray() ; //string to character array
//function calling
findBruteForce(text,pattern) ; //calls the findBruteForce function
findBoyerMoore(text,pattern) ; //calls the findBruteForce function
}
}
Output
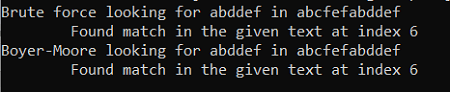
The above-displayed image is the output for the above program, and The output says that "abddef” is present in the “abcfefabddef” at index 6.
Let's use a Java program to implement the algorithm.
The Boyer Moore Java Program
Let's use a Java program to implement the Boyer-Moore algorithm and search pattern.
Program 1
Filename: BoyerMooreImplementation.java
public class BoyerMooreImplementation
{
static int NO_OF_CHARS = 256;
static int max (int a, int b)
{
return (a > b)? a: b;
}
static void badCharHeuristic( char []str, int size, int badchar[])
{
int i;
for (i = 0; i < NO_OF_CHARS; i++)
badchar[i] = -1;
for (i = 0; i < size; i++)
badchar[(int) str[i]] = i;
}
static void search( char txt[], char pat[])
{
int m = pat.length;
int n = txt.length;
int badchar[] = new int[NO_OF_CHARS];
//function calling
badCharHeuristic(pat, m, badchar);
int s = 0;
while(s <= (n - m))
{
int j = m-1;
while(j >= 0 && pat[j] == txt[s+j])
j--;
if (j < 0)
{
System.out.println("Patterns occur at character = " + s);
s += (s+m < n)? m-badchar[txt[s+m]] : 1;
}
else
s += max(1, j - badchar[txt[s+j]]);
}
}
public static void main(String args[])
{
//text in which pattern occurs
char txt[] = "123651266512".toCharArray();
//pattern to search
char pat[] = "12".toCharArray();
search(txt, pat);
}
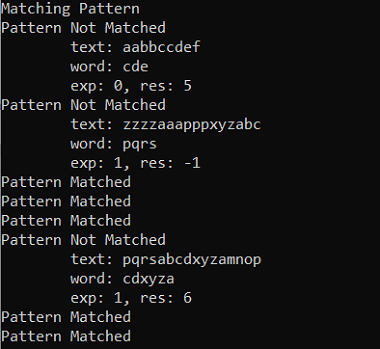
} Output
Let's look at another Java program where we have distinct logic for pattern finding implemented. The code that follows next determines whether the text contains the required pattern.
Program 2
Filename: BoyerMooreExample.java
public class BoyerMooreExample
{
public static void main(String args[])
{
System.out.println("Matching Pattern");
test("aabbccdef", "cde", 0);
test("zzzzaaapppxyzabc", "pqrs", 1);
test("mango", "ngo", 2);
test("abc", "d", -1);
test("catdog", "tdo", 2);
test("pqrsabcdxyzamnop", "cdxyza", 1);
test("cool", "", 0);
test("", "car", -1);
}
public static void test(String text, String word, int exp)
{
char[] textC = text.toCharArray();
char[] wordC = word.toCharArray();
int result = bm(textC, wordC);
if(result == exp)
System.out.println("Pattern Matched");
else
{
System.out.println("Pattern Not Matched");
System.out.println("\ttext: " + text);
System.out.println("\tword: " + word);
System.out.println("\texp: " + exp + ", res: " + result);
}//end of else
}//end of function
public static int[] makeD1(char[] pat)
{
int[] table = new int[255];
for(int i=0; i<255; i++)
table[i] = pat.length;
for(int i=0; i<pat.length-1; i++)
table[pat[i]] = pat.length-1-i;
return table;
}//end of the function
public static boolean isPrefix(char[] word, int pos)
{
int suffixlen = word.length - pos;
for(int i=0; i<suffixlen; i++)
if(word[i] != word[pos+i])
return false;
return true;
}//end of the function
public static int suffix_length(char[] word, int pos)
{
int i;
for(i=0; ((word[pos-i] == word[word.length-1-i]) & (i < pos)); i++)
{
}//end of for loop
return i;
}//end of the function
public static int[] makeD2(char[] pat)
{
int[] delta2 = new int[pat.length];
int p;
int last_prefix_index = pat.length - 1;
for(p = pat.length-1; p>=0; p--)
{
if(isPrefix(pat, p+1))
last_prefix_index = p+1;
delta2[p] = last_prefix_index + (pat.length-1-p);
}//end of for loop
for(p=0; p<pat.length-1; p++)
{
int slen = suffix_length(pat, p);
if(pat[p-slen] != pat[pat.length-1-slen])
delta2[pat.length-1-slen] = pat.length-1-p+slen;
}//end of for loop
return delta2;
}//end of function
public static int bm(char[] string, char[] pat)
{
int[] d1 = makeD1(pat);
int[] d2 = makeD2(pat);
int i = pat.length-1;
while(i < string.length)
{
int j = pat.length-1;
while(j>=0 && (string[i] == pat[j]))
{
i--; //decrement i by 1
j--; //decrement j by 1
}//end of while
if(j < 0)
return (i+1);
i += Math.max(d1[string[i]], d2[j]);
} //end of while
return -1;
}//end of the function
}
Output