Sliding Window Problem in Java

A sliding window is used in computer science and data science to process large datasets. It involves breaking the dataset into smaller chunks or windows and then processing it in each window. This is done by advancing the window by a certain amount each step, allowing the data to be processed more efficiently than if it were processed all at once. Sliding window techniques are commonly used in data streaming, signal processing, and natural language processing. By replacing nested loops with a single loop, the Window Sliding Technique seeks to reduce the utilisation of nested loops and hence the complexity of computing.

Example

For example, consider streaming sensor data that record temperatures every minute. To calculate the maximum temperature for the last hour, we could store the temperatures for the last 60 minutes in a sliding window. As a new temperature value is received, the oldest value is dropped from the window, and the new value is added. The maximum temperature can then be calculated from the remaining values in the window.

Problem Statement

A sliding window problem is a type of algorithm in which an array or string is processed in order to find a subset of elements which meet certain conditions. The sliding window algorithm is often used to find a subset of elements that, when summed, equal a certain value. For example, let's say we have an array A which contains the following elements: [1,15,1,2,6,12,5,7]. We want to find a subset of elements in A which, when summed, equal 3. Using the sliding window algorithm, we can start by taking the first two elements, 1 and 15, and summing them. If the sum is 3, we have found our subset and can stop. If the sum is not 3, we can move the window to the next pair of elements, 15 and 1, and sum them. This process continues until the sum is equal to 3 or until we reach the end of the array.

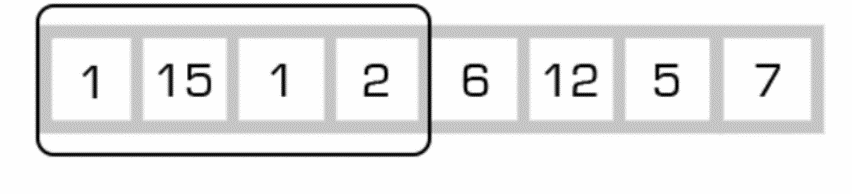
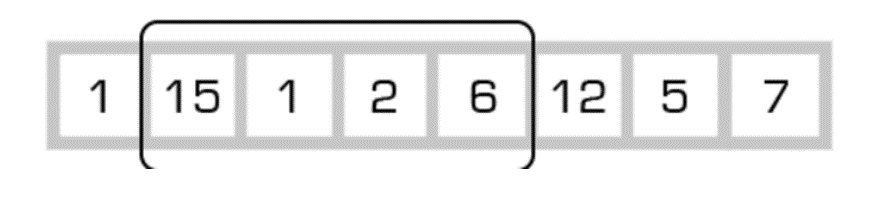
Algorithm

1. Initialize a window (a collection of elements) of size ‘k’.
2. Iterate over the elements of the array, one element at a time.
3. Add the current element to the window.
4. Remove the oldest element from the window.
5. Calculate the desired metric (for example, the sum of the elements) and record the result.
6. Repeat steps 2-5 until no more elements are processed.
7. Return the recorded results.

There are two types of Sliding window protocol

1. Fixed-size window
2. Variable size window

Fixed Size

The size of the required sub-array length is fixed. The size of the window should be only the given length. It cannot be altered.

Method

• An array is given, we want to determine the highest sum that fits inside the subarray size of k.
• First, we'll declare two variables: maxValue, which will save the highest value we can find, and currentWindowSum, which will record the window's current total.
• Until the window size is bigger than or equal to our specified window size of k, we shall iterate through the array and add each value onto our currentWindowSum.
• When this conditional is met, we will compare the maxValue to our currentWindowSum to determine which value is larger, and we will use that value as our new maxValue. Before iterating through our array and adding the next value, we will subtract the leftmost value.
• Then, we give back our maxValue

File Name : SlidingWindow.java

import java.util.*;
class SlidingWindow {


	// Returns maximum sum in a subarray of size k.
	static int maxSum(int arr[], int n, int k)
	{
		// if n is greater than window size k
		if (n < k) {
			System.out.println("Invalid");
			return -1;
		}


		// find sum of first window elements of size k 
		int max_sum = 0;
		for (int i = 0; i < k; i++)
			max_sum += arr[i];


		// Subtract the first element from the previous window and add the last element from the current window to calculate the sums of the remaining windows.
		int window_sum = max_sum;
		for (int i = k; i < n; i++) {
			window_sum += arr[i] - arr[i - k];
			max_sum = Math.max(max_sum, window_sum);
		}


		return max_sum;
	}


	// Main section of the program where execution begins
	public static void main(String[] args)
	{
		Scanner sc =new Scanner(System.in);
	    System.out.println("Enter size of the array ");
	    // storing the size of the array into the integer variable n
	    int n=sc.nextInt();
	    System.out.println("enter array elements ");
	    // storing array values into the array
	    int a[]=new int[n];
	    for(int i=0;i<n;i++)
	    {
	        a[i] = sc.nextInt();
	    }
	    // enter the size of the window 
	    System.out.println("Enter the size of the window");
		int k = sc.nextInt();
		// finding the length of the array 
		int l = a.length;
		// calling the function and printing the result
		System.out.println("The maximum subarray of size "+k+" is ");
		System.out.println(maxSum(a, l, k));
	}
}

Output

Enter size of the array 
10
enter array elements 
1 3 5 24 52 1 24 3 2 6
Enter the size of the window
3
The maximum subarray of size 3 is 
81

Variable Size

The window size can be altered in variable-size sliding windows based on the requirement.

Method

• This method is based on the minimum size subarray sum issue and applies to the variable window length example. We shall seek the smallest subarray that adds up to the desired value for this implementation.
• Executing a problem with a variable window size is trickier since we need to keep track of where our window starts and finishes with more variables. We'll first declare these four variables:

Variable	Requirement
minWindowSize	When we decide the smallest window size, we return this value. We must begin with a value that is much higher than our intended result.
currentWindowSum	minimum window size will be compared to the current window size.
windowStart	To determine the lowest value of our window,where our window begins.
windowEnd	To know the final minimum window value, we must always keep track of our window end.

Problem Statement

Find the index of 0 to be replaced with 1 in a binary array to obtain the longest possible continuous series of ones.

Take the array 0, 0, 1, 0, 1, 1, 1, 0, 1 as an illustration. To obtain a continuous sequence of length 6 that contains only 1s, the index that needs to be substituted is 8.

Method

Maintaining a window with a maximum of one zero at any given time while adding items from the right until the window becomes unstable is the goal. If there are two or more zeros in the window, it becomes unstable. If the window gets shaky, take away the elements on its left until it stabilises again. Update the index of 0 to be replaced if the window is stable and the current window length is greater than the largest window yet discovered.

File Name: SlidingWindow2.java

// importing the required packages
import java.util.*;
class SlidingWindow2
{
    //static declaration of the function to find the position of the index of the array
    public static int findIndexofZero(int[] A)
    {
        // declaration of the integer variables 
        int l = 0;      
        int c = 0;    
        int max_count = 0;  
 
        int ans = -1;         
        int prev_zero_index = -1;  
 
        for (int j = 0; j < A.length; j++)
        {
            
            if (A[j] == 0)
            {
                prev_zero_index = j;
                c++;
            }
 
        // the window becomes unstable if the total number of zeros in it becomes2
            if (c == 2)
            {
                // remove elements from the window's left side till we found a zero
                while (A[l] != 0) {
                    l++;
                }
 
                // remove the leftmost 0 so that window becomes stable again
                l++;
 
                // decrement count as 0 is removed
                c = 1;
            }
 
 
            if (j- l + 1 > max_count)
            {
                max_count = j - l + 1;
                ans = prev_zero_index;
            }
        }
 
        return ans;
    }
    // Main section of the program where execution begins
    public static void main (String[] args)
    {
        // creating object for scanner class
       Scanner sc =new Scanner(System.in);
       // enter the size of the array
	    System.out.println("Enter size of the array ");
	    // storing the size of the array into the integer variable n
	    int n=sc.nextInt();
	  // enter binary array elements
	    System.out.println("enter array elements ");
	    // storing array values into the array
	    int a[]=new int[n];
	    for(int i=0;i<n;i++)
	    {
	        a[i] = sc.nextInt();
	    }
	    // calling the function 
		System.out.println("The maximim index is");
	    System.out.println(findIndexofZero(a));


    }
}

Output

Enter size of the array 
7
enter array elements 
1 0 1 1 0 1 1
The maximum index is
4

Time Complexity

The above approach has an O(n) time complexity and uses no additional storage, where n is the length of the given sequence.