Self-Descriptive Numbers in Java
A number n is given. Identifying the self-descriptive numbers that exist between 1 and n is our task.
Self-Descriptive Numbers
The definition of a self-descriptive number, m, is a number with b digits in base b, with the most significant digit at 0 and the least significant digit at b - 1 (left to right with zero indexing, like an array). Additionally, every digit d is placed at n, calculating the number of times the digit n appears in m. Now, Look at the examples below.
A self-descriptive number is an integer n in base b that has b digits (the most significant digit at position 0 and the least significant at position b-1), and each digit at place p counts the frequency of that digit in n.
For instance, the number 6210001000 in base 10 is a self-descriptive number since it contains six 0s, two 1s, one 2, and one 6.
Explanation
The number is a base-10, a 10-digit number.
There are six 0s in the number 6210001000 and 6 at position 0.
There are two 1s in 6210001000, and it has a 2 at position 1.
It has a 1 at position 2 and one 2s in 6210001000.
There are zero 3s in 6210001000, and it has 0 at position 3.
There are zero 4s in 6210001000, and it has 0 at position 4.
There are zero 5s in 6210001000, and it has 0 at position 5.
There is one 6 in 6210001000 and 1 at position 6.
Example 1:
m = 2020
Output: 2020 is a self-descriptive number.
Explanation
Since 2020 only has four digits, base 4 is taken into consideration. Since the number 2 is in the 0th position, the number 0 appears twice. In the first slot, 0 indicates zero occurrences of 1. Again, 2 is in second place, which suggests that it occurs twice. Following that, 0 is put in the third position, meaning 3 doesn't appear (3 occurs zero times). When we look at the number, we learn that.
The number 0 appears twice. The number 2 appears twice. In addition, 1 and 3 don't happen at all. As a result, everything said in the paragraph above is true. 2020 is, therefore a self-descriptive number.
Example 2:
m = 6210001000
Output: 6210001000 is a self-descriptive number.
Explanation
Since 6210001000 only has ten digits, base 10 is taken into consideration. The fact that the number 6 is in the 0th position means that the number 0 appears six times. The fact that 2 is in the first place means that 1 is repeated twice. Once more, 1 appears in the second position, which indicates that 2 only occurs once. Following that, the positions 3, 4, 5, 7, 8, and 9 are all changed to 0s, which indicates that none of the numbers 3, 4, 5, 7, 8, or 9 occurred (occur zero times). The number 1, which denotes that the number 6 occurs just once, is in sixth place. If we look at the number, we discover that.
6 only occurred once. 2 have occurred just once. 1 is happening twice. 0 appears six times, while 2 only appears once. Also, there are no occurrences of 3, 4, 5, 7, 8, and 9 (occur zero times). As a result, the statements in the above paragraph are all true. Consequently, the number 6210001000 is a self-descriptive number.
Implementation: Using Nested Loop
Follow the instructions in the program below to find the self-descriptive number.
FileName: Example.java
// Printing self-descriptive number
// lying between 1 to 100000
public class Example
{
public boolean isSelfDescNum(int n)
{
// changing the integer n to the string str
String str = Integer.toString(n) ;
for (int k = 0; k < str.length(); k++)
{
// From the string, one by one, extract each digit
String tempChar = str.charAt(k) + "" ;
// changing the string (temChar) into an integer
// the variable v keeps the digit located at the index 'k'
int v = Integer.parseInt(tempChar) ;
// computing the number of times a specific-digit
// is occurring in the number n
int cnt = 0 ;
for (int p = 0; p < str.length(); p++)
{
// converting string char to integer
int tmp = Integer.parseInt(str.charAt(p) + "") ;
// check whether it is the same as the index 'k' or not
// if yes, then increase the count cnt.
if (tmp == k)
{
cnt = cnt + 1 ;
}
}
// If it is not the same
// then returning a false value.
if (cnt != v)
{
return false;
}
}
return true ;
}
// main method
public static void main(String argvs[])
{
int n = 100000 ;
// creating an object of the class SelfDescriptive
Example obj = new Example() ;
System.out.println("In the range 1 to " + n + ", we have the following self-descriptive numbers.");
for (int j = 1; j < n; j++)
{
if (obj.isSelfDescNum(j))
{
System.out.println(j) ;
}
}
}
}
Output
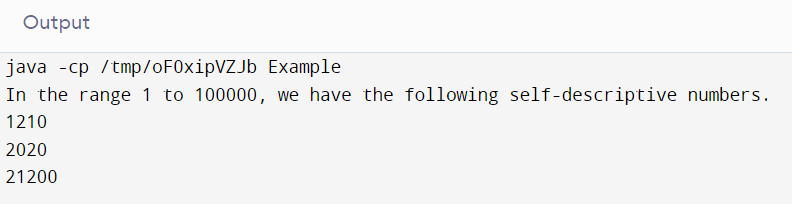
Explanation
Every time an iteration of the outer loop occurs, all of the digits are extracted and stored in the variable v. The number of occurrences of the number j (this j is the jth position of the outer loop) in the string is then calculated using a variable called cnt inside the inner loop. In the end, the variables cnt and v are contrasted. A false value is returned in the absence of a match in the comparison.
Complexity Analysis
The program has an O(n * len(n) * len(n)) time complexity. The program's space complexity is O(1).
The complexity of the program can be decreased if some preprocessing is done to store the frequency of the digits in an array. The following program provides an example of the same.
Filename: Example1.java
// Printing self-descriptive number
// lying between 1 to 100000
public class Example1
{
public boolean isSelfDescNum(int n)
{
String st = String.valueOf(n);
int j ;
// auxiliary array for storing the
// frequency count
int freqCount[] = new int[10] ;
for (j = 0; j < 10; j++)
{
freqCount[j] = 0 ;
}
while (n > 0)
{
freqCount[n % 10] = freqCount[n % 10] + 1;
n = n / 10 ;
}
for (j = 0; j < st.length(); j++)
{
// if the frequency count at the index j
// does not match the value at the
// index j present in the string st, then
// the given number n is not the self-descriptive
// number.
if (freqCount[j] != (st.charAt(j) - '0'))
{
return false ;
}
}
return true ;
}
// main method
public static void main(String argvs[])
{
int n = 100000 ;
// creating an object of the class SelfDescriptive1
Example1 obj = new Example1() ;
System.out.println("In the range 1 to " + n + ", we have the following self-descriptive numbers.");
for (int j = 1; j < n; j++)
{
if (obj.isSelfDescNum(j))
{
System.out.println(j);
}
}
}
}Output
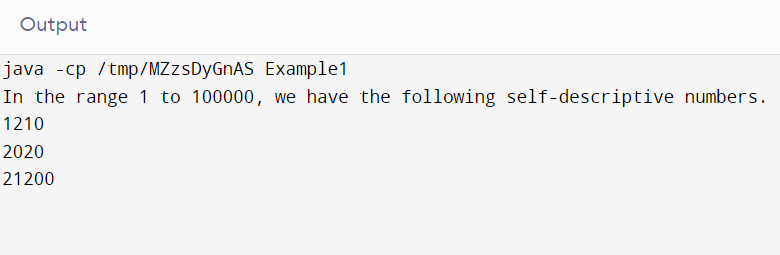
Complexity Analysis
The program's time complexity is O(n * len(n)). The program's space complexity is O(1). We are making use of an auxiliary array. The auxiliary array, however, is a size 10 array and does not change under any circumstances.
Here is the program to find descriptive numbers from the range 1 to n, where n is the user input.
Filename: Example2.java
// Printing self-descriptive number
// lying between 1 to the user input
import java.util.* ;
public class Example2
{
public boolean isSelfDescNum(int n)
{
String st = String.valueOf(n) ;
int j ;
// auxiliary array for storing the
// frequency count
int freqCount[] = new int[10] ;
for (j = 0; j < 10; j++)
{
freqCount[j] = 0 ;
}
while (n > 0)
{
freqCount[n % 10] = freqCount[n % 10] + 1 ;
n = n / 10 ;
}
for (j = 0; j < st.length(); j++)
{
// if the frequency count at the index j
// does not match the value at the
// index j present in the string st, then
// the given number n is not the self-descriptive
// number.
if (freqCount[j] != (st.charAt(j) - '0'))
{
return false ;
}
}
return true ;
}
// main method
public static void main(String argvs[])
{
Scanner sc=new Scanner(System.in) ;
int n =sc.nextInt();
// creating an object of the class SelfDescriptive1
Example2 obj = new Example2() ;
System.out.println("In the range 1 to " + n + ", we have the following self-descriptive numbers.");
for (int j = 1; j < n; j++)
{
if (obj.isSelfDescNum(j))
{
System.out.println(j) ;
}
}
}
}
Output
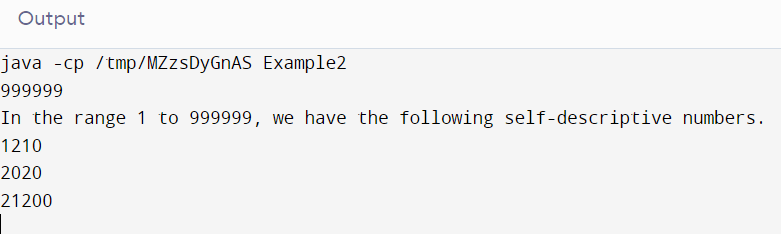
Complexity Analysis
The program's time complexity is O(n * len(n)). The program's space complexity is O(1). We are making use of an auxiliary array. The auxiliary array, however, is a size 10 array and does not change under any circumstances.