Hogben Numbers in Java

In this section, we will discover what the Hogben number is and develop Java programs that compute it. Java coding interviews and academic exams typically involve questions about the Hogben number program.

Hogben Number

The numbers that are recursively defined as follows are the Hogben numbers.

Where n >= 1 and H(0) = 1, H(n) = H(n-1) + 2 * (n-1)

Thus,

H(1) = H(1 - 1) + 2 * (1 - 1) = H(0) + 2 * 0 = 1 + 0 = 1

H(2) = H(2 - 1) + 2 * (2 - 1) = H(1) + 2 * 1 = 1 + 2 = 3

H(3) = H(3 - 1) + 2 * (3 - 1) = H(2) + 2 * 2 = 3 + 4 = 7

H(4) = H(4 - 1) + 2 * (4 - 1) = H(3) + 2 * 3 = 7 + 6 = 13

H(5) = H(5 - 1) + 2 * (5 - 1) = H(4) + 2 * 4 = 13 + 8 = 21

Let's examine the many methods for obtaining the Hogben numbers.

Recursive Approach

Let's look at how to find the first 10 Hogben numbers using a recursive method.

FileName: HogNum.java

public class HogNum   
{  
public int findHogNum(int n)  
{  
// handling the base case  
if(n == 1)  
{  
    return 1;   
}  
// recursively finding the nth Hogben number  
return (findHogNum(n - 1) + 2 * (n - 1));  
}  
  
// main method  
public static void main(String argvs[])  
{  
int n = 10;  
// creating an object of the class HogbenNum  
HogNum obj = new HogNum();  
System.out.println("The first " + n + " Hogben numbers are:");  
for (int j = 1; j <= n; j++)  
{  
int ans = obj.findHogNum(j);  
System.out.print(ans + " ");  
}  
}  
}  

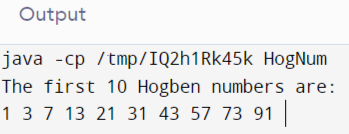
Output

Complexity Analysis

The time complexity of the code is O(n), where n is the nth number, according to complexity analysis. The program has constant space complexity, or O (1).

Iterative Approach

Take a look at the iterative method for obtaining the first 10 Hogben numbers.

FileName: HogNum1.java

public class Hognum1  
{  
// main method  
public static void main(String argvs[])  
{  
int n = 10;  
// auxiliary array for storing the Hogben numbers  
int dp[] = new int[n + 1];  
dp[0] = 1;  
System.out.println("The first " + n + " Hogben numbers are:");  
for (int j = 1; j <= n; j++)  
{  
// computing the Hogben numbers  
dp[j] = dp[j - 1] + 2 * (j - 1);  
System.out.print(dp[j] + " ");  
}  
}  
}  

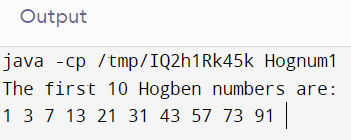
Output

Complexity Analysis

The program's time complexity is O (1). The program's space complexity is O(n), where n is the total number of Hogben numbers that need to be calculated.

The value of the most recent Hogben number computation is the single factor affecting the current Hogben number. Therefore, we are limited to using a variable to calculate the Hogben numbers rather than an array. See the code below.

FileName: HogNum2.java

public class HogNum2  
{  
// main method  
public static void main(String argvs[])  
{  
int n = 10;  
int temp = 1;  
System.out.println("The first " + n + " Hogben numbers are:");  
  
for (int j = 1; j <= n; j++)  
{  
// computing the Hogben numbers  
temp = temp + 2 * ( j - 1);  
System.out.print(temp + " ");  
}  
}  
}  

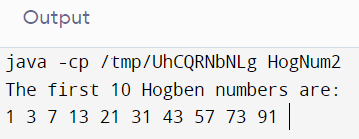
Output

Complexity Analysis

The program's time and space complexity are both O (1).

Using Mathematical Formula

The Hogben numbers are calculated using the following mathematical formula:

Where n >= 1, H(n) = n^2 - n + 1

Thus,

H(1) = 1^2 - 1 + 1 = 1 - 1 + 1 = 1

H(2) = 2^2 - 2 + 1 = 4 - 2 + 1 = 3

H(3) = 3^2 - 3 + 1 = 9 - 3 + 1 = 7

H(4) = 4^2- 4 + 1 = 16 - 4 + 1 = 13

H(5) = 5^2 - 5 + 1 = 25 - 5 + 1 = 21

The mathematical formula described above is used in the following code.

FileName: HogNum3.java

public class HogNum3  
{  
// main method  
public static void main(String argvs[])  
{  
int n = 10;  
  
System.out.println("The first " + n + " Hogben numbers are:");  
  
for (int j = 1; j <= n; j++)  
{  
// computing the Hogben numbers  
int ans = (j * j) - j + 1;  
System.out.print(ans + " ");  
}  
}  
}  

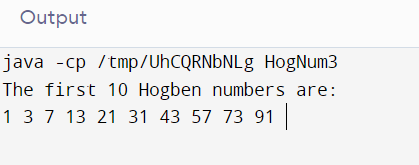
Output

Complexity Analysis

The program's time and space complexity are both O (1).