Graph Problems in Java

A graph is a special type of data structure used in programming that is made up of edges connecting each set of finitely many nodes, or vertices, to each other. The vertices connected to the same edge might be called adjacent vertices. A graph is only a graphic depiction of vertices and edges connecting. Even though there are numerous graph algorithms, some of which you may be aware of, only a few are used. The simple explanation is that traditional graph algorithms are built to answer millions of problems with just a few lines of logically programmed code.

Components of Graph

Vertices:

The basic building blocks of a graph are called vertices. Vertices are sometimes referred to as nodes or vertices. Any node or vertex can have a label or not.

Edges:

In a graph, edges are lines that link two nodes together. In a directed graph, it may be an ordered pair of nodes. Edges can connect any two nodes in any manner. No regulations exist. Edges are sometimes also referred to as arcs. Any edge may be labeled or left unlabelled. 

Many problems in everyday life can be resolved with graphs. Networks are depicted using graphs. The networks could be telephone, circuit, or city-wide path networks.

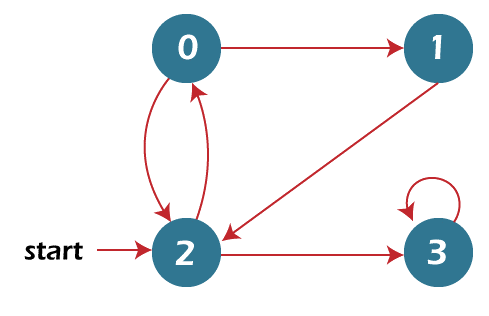
1. BFS Traversal

Most graph theory issues can be resolved via breadth-first search. To find a node in a tree or graph data structure that meets a set of requirements, the breadth-first search (BFS) technique is used. Before moving on to the nodes at the following depth level, it originates at the tree's root or graph and searches/visits every node at the current depth level.

The only problem with this is that graphs might have cycles, unlike trees, so we might keep going back to the same node. We categorize the vertices into two groups to avoid processing a node twice:

• visited
• unvisited

The visited vertices are noted using a boolean visited array. All vertices are considered to be reachable from the initial vertex for simplicity. For traversal, BFS employs a queue data structure.

Pseudocode

Breadth-first_search (graph, A) //Here, X is the source node, and Graph is the graph we already have. 


Using Q as the queue 
Marking the source node A as visited by calling 
Q.enqueue(A) 


While ( Q is not empty ) ( Q is not empty ) 
The front node is eliminated from the queue when Y = Q.dequeue(). 
Process each neighbour of Y and each neighbour of Z of Y. 
Enqueue(Z) //Stores Z in Q if Z is not visited. 
Mark Z has traveled

Filename: Graphs.java

// BFS traversal from a specified source vertex is printed by a Java program. 
//BFS(int s) travels between vertices that can be reached from s.
import java.io.*;
import java. util.*;
// the graphs representation using the adjacency list
class Graphs {
	private int Vertex; // denoting the no of vertices
	private LinkedList<Integer> adjacent[]; // The Adjacent lists
	Graphs(int ve)
	{
		Vertex = ve;
		adjacent = new LinkedList[ve];
		for (int i = 0; i < ve; ++i)
			adjacent[i] = new LinkedList();
	}
	// the method which will add an edge to the graph
	void addEdges(int ve, int we) 
	{ 
	    adjacent[ve].add(we); 
	}
	// the result of the bfs traversal of the graph
	void BFS(int so)
	{
		//The unvisited nodes are marked as false by default.
		boolean visiteds[] = new boolean[Vertex];
		// The queue for storing the values that will come next
		LinkedList<Integer> queues = new LinkedList<Integer>();
		// Mark the current node as visited and enqueue it
		visiteds[so] = true;
		queues.add(so);
		while (queues.size() != 0) {
			// the vertex value is removed from the queue
			so = queues.poll();
			System.out.print(so + " ");
			// Get each of the dequeued vertex's surrounding vertices. 
			//If an adjacent node hasn't been visited, 
			//mark this as visited and add it to the queue.
			Iterator<Integer> in = adjacent[so].listIterator();
			while (in.hasNext()) {
				int num = in.next();
				if (!visiteds[num]) {
					visiteds[num] = true;
					queues.add(num);
				}
			}
		}
	}


	//Main section of the program
	public static void main(String args[])
	{
		Graphs gr = new Graphs(4);


		gr.addEdges(0, 1);
		gr.addEdges(0, 2);
		gr.addEdges(1, 2);
		gr.addEdges(2, 0);
		gr.addEdges(2, 3);
		gr.addEdges(3, 3);


		System.out.println( "The Breadth First Traversal for the given nodes “ + "(The initial node is at 2): ");


		gr.BFS(2);
	}
}

Output

The Breadth First Traversal for the given nodes (The initial node is at 2)
2 0 3 1 

Time Complexity: O(V+E)

Space Complexity: O(V)

2. DFS Traversal

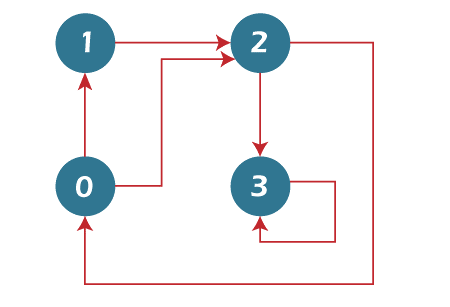
Multiple DFS traversals are possible for a graph. A graph's Depth First Traversal (or Search) is comparable to a tree's Depth First Traversal. The main problem with this is that, unlike trees, graphs can also contain cycles (a node may be visited twice). Use a boolean visited array to prevent processing a node twice.

An algorithm for traveling or searching through tree or graph data structures is called depth-first search. The algorithm begins at the root node (choosing an arbitrary node to serve as the root of the tree in the case of a graph) and proceeds to investigate each branch as far as it can go before turning around.

Thus, the basic concept is to begin at the root or any other random node, mark that node, then advance to the next nearby node that is not marked. This process is repeated until there are no more unmarked adjacent nodes. Then go back and look for more unmarked nodes to cross. Print the path's nodes, and lastly.

To solve the problem, follow the instructions listed below:

• Make a recursive function that accepts a visited array and the node's index.
• Print the node and indicate that it has been visited.
• Using the index of the adjacent node as the argument, traverse all nearby and unmarked nodes before calling the recursive method.

Filename: DfsGraph.java

//Java Program for finding the DFS path of the graph
import java.io.*;
import java.util.*;
// The class consists of DFS adjacency lists
class DfsGraph {
	private int Vertex; // denotes the number of vertices in the graph
	// An array for storing the adjacency lists
	private LinkedList<Integer> adjacent[];
	@SuppressWarnings("unchecked") DfsGraph(int ve)
	{
		Vertex = ve;
		adjacent = new LinkedList[ve];
		for (int i = 0; i < ve; ++i)
			adjacent[i] = new LinkedList();
	}
	//the function for adding the vertex
	void addEdges(int ve, int we)
	{
		adjacent[ve].add(we); // The we is added the list
	}
	// The logic of DFS
	void DFSUtils(int ve, boolean visiteds[])
	{
		// The node visited is then marked and is printed
		visiteds[ve] = true;
		System.out.print(ve + " ");
		//The recurrence will follow all the vertices left
		Iterator<Integer> in = adjacent[ve].listIterator();
		while (in.hasNext()) {
			int num = in.next();
			if (!visiteds[num])
				DFSUtils(num, visiteds);
		}
	}
	// the recursive function of DFS
	void DFS(int ve)
	{
		// The unvisited nodes are marked as false
		boolean visiteds[] = new boolean[Vertex];
		// The recursive will print the path
		DFSUtils(ve, visiteds);
	}
	// Main section of the program
	public static void main(String args[])
	{
	    DfsGraph gr = new DfsGraph(4);
		gr.addEdges(0, 1);
		gr.addEdges(0, 2);
		gr.addEdges(1, 2);
		gr.addEdges(2, 0);
		gr.addEdges(2, 3);
		gr.addEdges(3, 3);
		System.out.println( "The Depth First Traversal” + "( The initial vertex is 2)");
		// the function calling
		gr.DFS(2);
	}
}

Output

The Depth First Traversal( The initial vertex is 2)
2 0 1 3

Time Complexity: O(V+E)

Where V is the vertex and  E is the Edges of the graph.

Space Complexity: O(V)

3. Dijkstra’s Shortest Path for the given Graph

Problem statement:

Find the shortest routes between a source vertex and each vertex in the provided graph, the graph, and the source vertex.

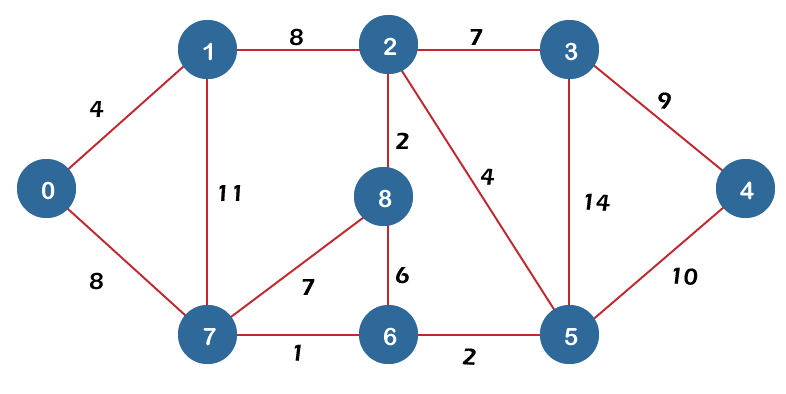
Dijkstra's algorithm and Prim's approach for the minimum spanning tree are extremely similar.

Create an SPT (shortest path tree) using the specified source as the root, similar to Prim's MST. Maintain two sets, one of which contains vertices already included in the shortest-path tree and the other of which contains yet to be included. Locate a vertex with a minimum distance to the source that is also a member of the other set and is present at each iteration of the method.

To solve that problem, follow the instructions listed below:

• Make a set called sptSet (shortest tree sets) that records the vertices that are part of the shortest-path tree, meaning that their minimum distance from the source has been determined and is definitive. This set is initially empty.
• Give each vertex in the input network a distance value. Set the source vertex's distance value to 0 to ensure it is chosen first. Set all distance values to INFINITE at the beginning.
• While not all vertices are present in sptSet

 Choose a vertex u with a minimum distance value absent from the sptSet.

Add you to the sptSet.

 Update all vertices of u's neighboring triangle's distance value after that.

 If the distance value of v for a given neighboring vertex is less than the total distance value of u (from the source) and the weight of the   

edge u-v, then the distance value of v should be updated. Repeat this process for all neighboring vertices to update the distance values.

The collection of vertices that make up SPT is represented by the boolean array sptSet[]. Vertex v is included in SPT if sptSet[v] has a true value; otherwise, it is not. The shortest distance measurements of each vertex are kept in the array dist[].

Java Program for the above implementation

Filename: ShortestPaths.java

//Java program for the single source shortest route algorithm developed by Dijkstra. 
//The program represents a graph using an adjacency matrix.
import java.io.*;
import java.lang.*;
import java.util.*;
class ShortestPaths{
	//A useful function that searches the set of vertices not yet contained in the //shortest path tree for the vertex with the lowest distance value.
	static final int Vertex = 9;
	int minDistance(int distance[], Boolean sptSets[])
	{
		// the min value is initialized
		int minimum = Integer.MAX_VALUE, min_indexs = -1;


		for (int ve = 0; ve < Vertex; ve++)
			if (sptSets[ve] == false && distance[ve] <= minimum) {
				minimum = distance[ve];
				min_indexs = ve;
			}
		return min_indexs;
	}
	// a function for the distance calculation
	void printSolution(int distance[])
	{
		System.out.println(
			"The Vertex \t\t The Distance from the Source Vertex");
		for (int i = 0; i < Vertex; i++)
			System.out.println(i + " \t\t " + distance[i]);
	}
	// Adjacency matrix representation of a graph //with Dijkstra's single source algorithm //for shortest paths implemented
	void dijkstras(int graphs[][], int srcs)
	{
		int distance[] = new int[Vertex]; //  the result array
			//The shortest path from src to I will be held by dist[i]. 
            //,If vertex I am part of the shortest path tree or the finalized//shortest path from source to vertex I then sptSet[i] would be true.
		Boolean sptSets[] = new Boolean[Vertex];
		// the initial distance is used
		for (int i = 0; i < Vertex; i++) {
			distance[i] = Integer.MAX_VALUE;
			sptSets[i] = false;
		}
		// the distance from the source itself is 0
		distance[srcs] = 0;


		// the loop for the shortest path 
		for (int counts = 0; counts < Vertex - 1; counts++) {
			// Choose the unprocessed vertex with the smallest distance from the collection. 
			//In the initial iteration, u1 is always identical to src.
			int u1 = minDistance(distance, sptSets);
			//The vertex that has been visited is marked off
			sptSets[u1] = true;
			// the value of the current vertex is updated
			for (int ve = 0; ve < Vertex; ve++)
				// Refresh distance[ve] Only if it is not in sptSets, there is a //path from u1 to ve, and the weight of all paths     
                                            from src //to ve through u1 is less than the value of distacen[ve] at the moment.
				if (!sptSets[ve] && graphs[u1][ve] != 0
					&& distance[u1] != Integer.MAX_VALUE
					&& distance[u1] + graphs[u1][ve] < distance[ve])
					distance[ve] = distance[u1] + graphs[u1][ve];
		}
		// The array is created
		printSolution(distance);
	}
	// Main section of the program
	public static void main(String[] args)
	{
		// An example graph of the above values
		int graphs[][]
			= new int[][] { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
							{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
							{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
							{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
							{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
							{ 0, 0, 4, 14, 10, 0, 2, 0, 0 },
							{ 0, 0, 0, 0, 0, 2, 0, 1, 6 },
							{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
							{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
		ShortestPaths te = new ShortestPaths();


		// Function call
		te.dijkstras(graphs, 0);
	}
}

Output

The Vertex 		 The Distance from the Source Vertex
0 		 0
1 		 4
2 		 12
3 		 19
4 		 21
5 		 11
6 		 9
7 		 8
8 		 14

Time Complexity: O(V*2)

Space Complexity: O(V)

Note:

• The code determines the shortest path. However, it doesn't determine the distance. To display the shortest path from the source to several vertices, make a parent array, update it as the distance changes (similar to how prim implemented this), and then use it.

• Although the Dijkstra function is used in the code for undirected graphs, it may also be used for directed graphs.

• The code determines which vertices are closest to the source. When the chosen lowest distance vertex is identical to the target, break them for a loop if we are only interested in the smallest route between the source and a single target.

4. Find the shortest routes from a particular source vertex (src) to every vertex within the provided graph. Negative weight edges could be present in the graph using the bellman-ford Algorithm.

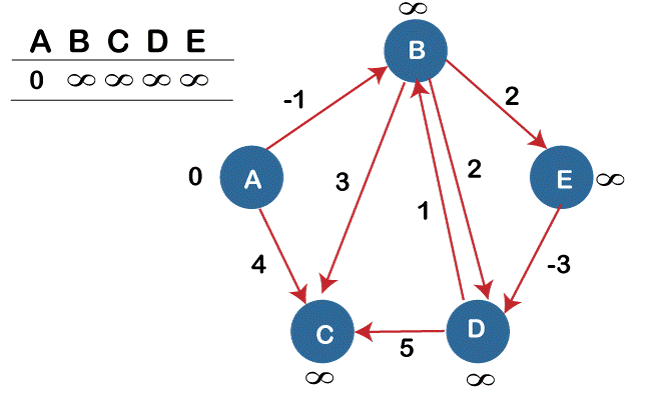
Bellman-Ford applies to negatively weighted graphs, although Dijkstra is not. Dijkstra is more complicated than Bellman-Ford, which is why it works well for distributed systems.

The Bellman-Ford algorithm's steps for determining the shortest path from the source to each vertex are as follows:

• This step initializes the source's distance to every vertex as infinite and the source's distance as zero.
  Make an array dists[] of size |Vs. | except for dists[src]—the source vertex—having all values set to infinite.

• The shortest distances are computed in this stage. Where |V| is the number of vertices in the given graph, perform the following |V|-1 times. Apply the following to each edge. u-v
  Update dists[v] to dists[v] = dists[u] + weight of edge uv if dists[v] > dists[u] + weight of edge UV.

• If a negative weight cycle is present on the graph, the following step displays it. Repeat the process for each edge, performing the steps u-v with each edge. The statement "Graph has negative weight cycle" is true if dist[v] > dist[u] + weight of edge UV.  The logic behind step 3 is that if the graph does not have a negative weight cycle, step 2 ensures the shortest distances. Obtaining a shorter path for every vertex after iterating through all edges once more results in a negative weight cycle.

Filename: BellmanFordGraph.java

//Program for finding the shortest path using BellmanFord Algorithm
//importing packages
import java.io.*;
import java.lang.*;
import java.util.*;
//A class for representing the vertices and edges of the graph
class BellmanFordGraph {


	// Graph which describes the edges
	class Edges {
		int srcs, dests, weights;
		Edges() { srcs = dests = weights = 0; }
	};


	int Vs, Es;
	Edges edge[];


	// Creates a graph with V vertices and E edges
	BellmanFordGraph(int v1, int e1)
	{
		Vs = v1;
		Es = e1;
		edge = new Edges[e1];
		for (int i = 0; i < e1; ++i)
			edge[i] = new Edges();
	}


	// the primary function that applies the Bellman-Ford algorithm to discover the shortest distances between 
	// src and all other vertices. Additionally, the function may identify negative weight cycles.
	void BellmanFord(BellmanFordGraph graph, int srcs)
	{
		int Vs = graph.Vs, Es = graph.Es;
		int dists[] = new int[Vs];


		// the initial vertex is initialized and all set to infinite
		for (int i = 0; i < Vs; ++i)
			dists[i] = Integer.MAX_VALUE;
		dists[srcs] = 0;


		// Step 2: Relax all edges |Vs| - 1 times. A simple
		// shortest of the path from srcs to any other vertex can
		// have an at-most |Vs| - 1 edge
		for (int i = 1; i < Vs; ++i) {
			for (int j = 0; j < Es; ++j) {
				int u1 = graph.edge[j].srcs;
				int v1 = graph.edge[j].dests;
				int weights = graph.edge[j].weights;
				if (dists[u1] != Integer.MAX_VALUE
					&& dists[u1] + weights < dists[v1])
					dists[v1] = dists[u1] + weights;
			}
		}


		// Step 3: Look for negative weight cycles.
		//The above procedure ensures the shortest distances if a graph doesn't contain negative weight cycles. 
		//There is a cycle if we obtain a shorter path.
		for (int j = 0; j < Es; ++j) {
			int u1 = graph.edge[j].srcs;
			int v1 = graph.edge[j].dests;
			int weights = graph.edge[j].weights;
			if (dists[u1] != Integer.MAX_VALUE
				&& dists[u1] + weights < dists[v1]) {
				System.out.println(
					"The Graph has negative weights cycle");
				return;
			}
		}
		printArrs(dists, Vs);
	}


	//A function for printing the result
	void printArrs(int dists[], int Vs)
	{
		System.out.println("The Distance of the vertex from the source");
		for (int i = 0; i < Vs; ++i)
			System.out.println(i + "\t\t" + dists[i]);
	}


	//Main section of the program
	public static void main(String[] args)
	{
		int Vs = 5; // Declaring the number of vertices in the graph
		int Es = 8; // Declaring the number of edges in the graph


		BellmanFordGraph graph = new BellmanFordGraph(Vs, Es);
		// the edges are added to the graph
		graph.edge[0].srcs = 0;
		graph.edge[0].dests = 1;
		graph.edge[0].weights = -1;


		// the edges are added to the graph
		graph.edge[1].srcs = 0;
		graph.edge[1].dests = 2;
		graph.edge[1].weights = 4;


		//the edges are added to the graph
		graph.edge[2].srcs = 1;
		graph.edge[2].dests = 2;
		graph.edge[2].weights = 3;


		// the edges are added to the graph
		graph.edge[3].srcs = 1;
		graph.edge[3].dests = 3;
		graph.edge[3].weights = 2;


		//the edges are added to the graph
		graph.edge[4].srcs = 1;
		graph.edge[4].dests = 4;
		graph.edge[4].weights = 2;


		// the edges are added to the graph
		graph.edge[5].srcs = 3;
		graph.edge[5].dests = 2;
		graph.edge[5].weights = 5;


		// the edges are added to the graph
		graph.edge[6].srcs = 3;
		graph.edge[6].dests = 1;
		graph.edge[6].weights = 1;


		//the edges are added to the graph
		graph.edge[7].srcs = 4;
		graph.edge[7].dests = 3;
		graph.edge[7].weights = -3;
		
		// Function calling
		graph.BellmanFord(graph, 0);
	}
}

Output

The Distance of the vertex from the source
0		0
1		-1
2		2
3		-2
4		1

5. Find the size of the largest region in the Boolean Matrix

Problem:

Consider a matrix in which each cell is either a "0" or a "1," with every cell having a 1 being referred to as a "filled cell." A connection exists between two cells when they are placed next to one another either horizontally, vertically, or diagonally. A region is created when several connected filled cells become one. Identify the biggest region's size.

Approach: DFS

To find the solution, according to the directions provided:

• In a 2D matrix, a cell can connect to a maximum of 8 neighbors.
• Make recursive calls to the cell's eight neighbors in DFS.
• To keep track of all visited cells, establish a visited Hash-map.
• Additionally, update the maximum size region and keep a record of the visited 1s in each DFS.

Example:

Input: M[][5] = { {1, 0, 1, 1, 0}, {1, 0, 1, 1, 0}, {0, 1, 0, 0, 1}, {0, 1, 0, 0, 1}}

Output: 5

The example has only 2 regions; one has  1 as size, and the other has 5 in size.

Filename: LargestRegion.java

// Java Program for finding the largest region length in a 2-D matrix
//importing packages
import java.io.*;
import java. util.*;
class LargestRegion{
	static int ROWS, COLS, counts;
	// a function to determine whether a specific cell (row, col) 
	// can be used in DFS
	static boolean isSafes(int[][] M1, int rows, int cols, boolean[][] visiteds)
	{
		// the value is 1 and has not yet been visited, and the rows.
		//number and column number are both in the range.
		return (
			(rows >= 0) && (rows < ROWS) && (cols >= 0)
			&& (cols < COLS)
			&& (M1[rows][cols] == 1 && !visiteds[rows][cols]));
	}


	// a useful function for performing DFS on a 2D boolean matrix. 
	//It merely considers the eight neighbors as "adjacent nodes."
	static void DFS(int[][] M1, int rows, int cols,boolean[][] visiteds)
	{
		// These fields are used to retrieve the row and column/numbers
		//of a particular cell's eight neighbors.
		int[] rowNbrs = { -1, -1, 1, 0, 0, 1, 1, 1 };
		int[] colNbrs = { -1, 0, 1, -1, 1, -1, 0, 1 };


		//Marking the visited node
		visiteds[rows][cols] = true;
		// Recurrence of all connected nodes
		for (int ks = 0; ks < 8; ks++) {
			if (isSafes(M1, rows+ rowNbrs[ks], cols + colNbrs[ks],
					visiteds)) {
				// The region is then incremented to 1
				counts++;
				DFS(M1, rows + rowNbrs[ks], cols + colNbrs[ks],
					visiteds);
			}
		}
	}


	// The primary function of a given boolean 2D matrix that returns the longest length region is
	static int largestRegion(int[][] M1)
	{
		// Create a boolean array to record the visited cells. 
		//At first, none of the cells are visited.
		boolean[][] visiteds = new boolean[ROWS][COLS];
		// Declare the results as 0 and iterate through 
		// all of the cells in the provided matrix
		int results = 0;
		for (int i = 0; i < ROWS; i++) {
			for (int j = 0; j < COLS; j++) {


				// checking with 1
				if (M1[i][j] == 1 && !visiteds[i][j]) {
					//after that, a new region was discovered.
					counts = 1;
					DFS(M1, i, j, visiteds);


					// maximum region
					results = Math.max(results, counts);
				}
			}
		}
		return results;
	}
	//Main section of the program
	public static void main(String args[])
	{
		int M1[][] = { { 1, 0, 1, 1, 0 },
					{ 1, 0, 1, 1, 0 },
					{ 0, 1, 0, 0, 1 },
					{ 0, 1, 0, 0, 0 } };
		ROWS = 4;
		COLS = 5;


		// Function calling
		System.out.println(largestRegion(M1));
	}
}

Output

5