Permutation Coefficient in Java
In this tutorial, we will get familiar with the permutation coefficient in Java. We will understand it through examples and see different approaches to solving the problem.
A permutation is a term used mainly in mathematics and it finds usage in programming as well. It can be defined as the method of ordering each member of a provided set to form an arrangement. P(n, r) is used to represent a permutation coefficient. N refers to the total no. of elements and r represents an instance, which means it gives out the total number of permutations by considering r at a time.
For example:
P(6,2) – It means there are 6 elements as n is equal to 6 and 2 elements can be taken from it as r is equal to 2.
To know what the possible arrangements are or how these 2 numbers can be arranged, we need to take permutation into account.
Considering 6 elements 1, 2, 3, 4, 5, 6 and taking 2 elements at a time.
The possible arrangements become:
(1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6)
(2, 1)(2, 2)(2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2)(3, 3) (3, 4) (3, 5) (3, 6)
(4, 1) (4, 2) (4, 3)(4, 4)(4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4), (5, 5) (5, 6)
On counting the above-written pairs we receive 25. It denotes that there are 25 ways to arrange the numbers from 1 to 6 by considering 2 at a time.
Now, let us look at the mathematical way to solve the above problem P(n, r).
One can easily solve it using the given formula:
P(n, r) = n! / (n - r)!
P(6, 2) = 6! / (6 - 2)! = 6! / 4! = (6 x 5 x 4 x 3 x 2 x 1) / (4 x 3 x 2 x 1) = 720 / 24 = 30
Now, let us understand the concept through a java program
Implementation
public class PermCoefficient
{
// a method to compute the factorial
// of the number n,which is n!
public int computeFactorial(int num)
{
int res = 1;
// loop to compute the value of
// 1 x 2 x 3 x 4 x ... x n
for(int j = 1; j <=num; j++)
{
res = res * j;
}
return res;
}
public int computePermutation(int num, int r1)
{
// finding factorial till n
int numerator = computeFactorial(num);
// computing factorial (num - r1)!
int denominator = computeFactorial(num - r1);
/// computing P(num, r1) = num! / (num - r1)!
return (numerator / denominator);
}
// main method
public static void main(String argvs[])
{
int num = 8;
int r1 = 5;
// creation of an object of the class named PermCoefficient
PermCoefficient obj = new PermCoefficient();
// storing the outcome of the function computePermutation()
int answer = obj.computePermutation(num, r1);
// displaying the answer
System.out.println("The value of (" + num + ", " + r1 + ") is: " + answer);
num = 7;
r1 = 3;
System.out.println();
// keeping the result of the method findPermutation() in a variable
answer = obj.computePermutation(num, r1);
// displaying the outcome
System.out.println("The value of (" + num + ", " + r1 + ") is: " + answer);
}
} Output:
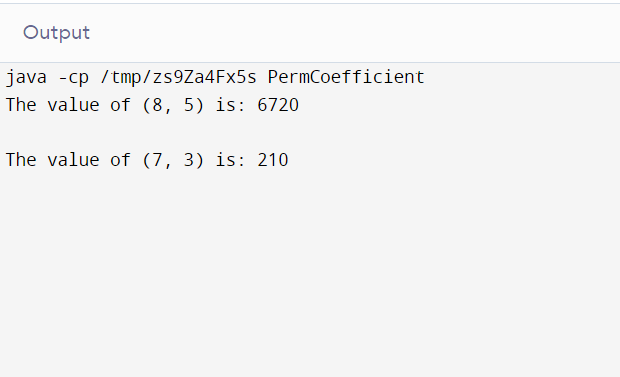
Explanation: When n is 8 and r is 5, the possible number of outcomes would be 6720.Similarly, if the value of n is 7 and the value of r is 3 then, the possible number of arrangements would be 210.
The time complexity of this program is O(n + r).
The second approach - Recursive
public class PermutationCoeff
{
// A method to compute the value of P(n, r), recursively
public int computePermutationCoeff(int num, int r1)
{
// dealing with the base cases
if(r1 == 0)
{
return 1;
}
else if(r1 == num)
{
// computing the value of num!
int res = 1;
for(int j = 1; j <= num; j++)
{
res = res * j;
}
return res;
}
else
{
// finding the value of P(num, r1) with the help of the recursion formula
return computePermutationCoeff(num - 1, r1) + r1 * computePermutationCoeff(num - 1, r1 - 1);
}
}
// main method
public static void main(String argvs[])
{
int num = 15;
int r1 = 3;
// creation of an object of the class named PermutationCoeff
PermutationCoeff obj = new PermutationCoeff();
// calling the function computePermutationCoeff()
int res = obj.computePermutationCoeff(num, r1);
System.out.println("The Value of P(" + num + ", "+ r1 +")" + " = " + res);
// updating the value of num & r1
num = 9;
r1 = 4;
System.out.println();
// calling the function computePermutationCoeff()
res = obj.computePermutationCoeff(num, r1);
System.out.println("The Value of P(" + num + ", "+ r1 +")" + " = " + res);
}
} Output:
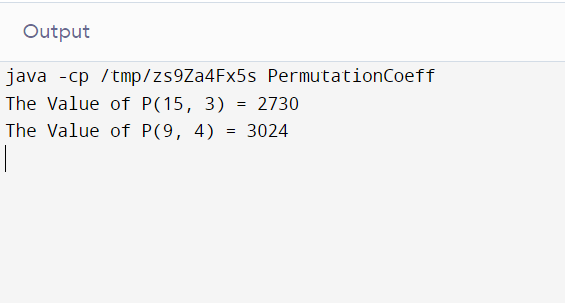
Explanation: In this approach, we tried to solve the problem recursively.
Third approach: Iterative1
public class PermutationCoeff3
{
// A function to find the result of P(num, r1)
public int computePermutationCoeff(int num, int r1)
{
int Fn2 = 1;
int Fr2 = 1;
// Calculaing num! and (num - r1)!
for (int j = 1; j <= num; j++)
{
Fn2 = Fn2 * j;
if (j == num - r1)
{
Fr2 = Fn2;
}
}
int res = Fn2 / Fr2;
return res;
}
// main method
public static void main(String argvs[])
{
int num = 15;
int r1 = 3;
// creation of an object of the class named PermutationCoeff3
PermutationCoeff3 obj = new PermutationCoeff3();
// calling the funcion computePermutationCoeff()
int res1 = obj.computePermutationCoeff(num, r1);
System.out.println("The Value of P(" + num + ", "+ r1 +")" + " = " + res1);
// updating the value of num and r1
num = 9;
r1 = 2;
System.out.println();
// calling the function computePermutationCoeff()
res1 = obj.computePermutationCoeff(num, r1);
System.out.println("The Value of P(" + num + ", "+ r1 +")" + " = " + res1);
}
}
Output:

Explanation: In this method, a nested for loop and a two-dimensional array is used. The time complexity here is O(n * r). The space complexity is also the same i.e O(n * r). However, we can reduce these complexities by optimizing our program.
4th approach: iterative2
public class PermutationCoeff2
{
// A method that calculates the value of P(num, r1)
public int computePermutationCoeff(int num, int r1)
{
int a[] = new int[num + 2];
// Computing the value of the Permutation Coefficient
//in abottom-up manner
for (int i = 0; i <= num; i++)
{
// dealing with the Base Case
if (i == 0)
{
a[i] = 1;
}
// Compute the value using the previously
// stored values
else
{
a[i] = a[i - 1] * i;
}
}
// calculating num! / (num - r)!
int res = a[num] / a[num - r1];
return res;
}
// main method
public static void main(String argvs[])
{
int num = 15;
int r1 = 3;
// creation of an object of the class PermutationCoeff2
PermutationCoeff2 obj = new PermutationCoeff2();
// calling the method named computePermutationCoeff()
int result = obj.computePermutationCoeff(num, r1);
System.out.println("The Value of P(" + num + ", "+ r1 +")" + " = " + result);
// upadating the value of num & r1
num = 9;
r1 = 2;
System.out.println();
// calling the method named computePermutationCoeff()
result = obj.computePermutationCoeff(num, r1);
System.out.println("The Value of P(" + num + ", "+ r1 +")" + " = " + result);
}
} Output:
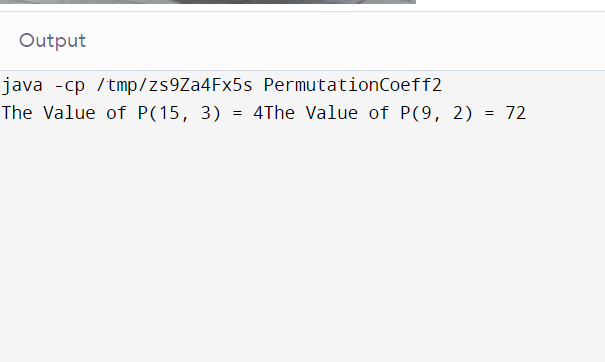
Explanation: In this case, the space and time complexity have been reduced to O(n).
5th approach: iterative3
public class PermutationCoeff3
{
// A method to calculate the value of P(num, r1)
public int computePermutationCoeff(int num, int r1)
{
int Fn1 = 1;
int Fr1 = 1;
// Calculating num! and (num - r1)!
for (int j = 1; j <= num; j++)
{
Fn1 = Fn1 * j;
if (j == num - r1)
{
Fr1 = Fn1;
}
}
int ans = Fn1 / Fr1;
return ans;
}
// main method
public static void main(String argvs[])
{
int num = 15;
int r1 = 3;
// creation an object of the class named PermutationCoeff3
PermutationCoeff3 obj = new PermutationCoeff3();
// calling the function named computePermutationCoeff()
int result = obj.computePermutationCoeff(num, r1);
System.out.println("The Value of P(" + num + ", "+ r1 +")" + " = " + result);
// upadating the value of n & r
num = 9;
r1 = 4;
System.out.println();
// calling the function named computePermutationCoeff()
result = obj.computePermutationCoeff(num, r1);
System.out.println("The Value of P(" + num + ", "+ r1 +")" + " = " + result);
}
} Output:
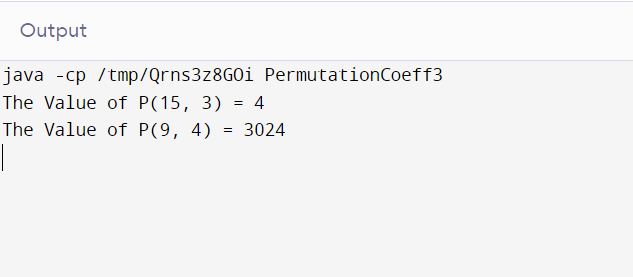
Explanation: In this iterative approach, the time and space complexity is reduced to O(1). So, this is the most optimized approach to solve the given problem.