Print Matrix Diagonally in Java

The aim is to print the elements of a matrix of size n*n in some kind of a diagonal pattern.

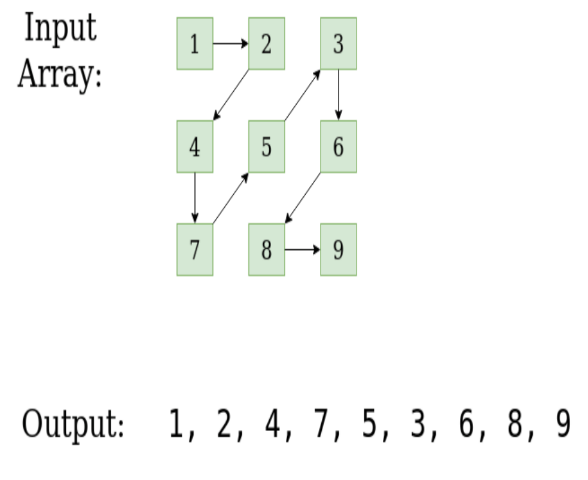
Input : mat[3][3] = {{1, 2, 3},

                     {4, 5, 6},

                     {7, 8, 9}}

Output : 1 2 4 7 5 3 6 8 9.

Explanation: Starting from the number 1

then diagonally from above to below that is 2 and 4

then diagonally upward from below that is 7, 5, 3

then diagonally from top to bottom that is  6, 8

Next, go up till you reach the end 9.

Input :  mat[4][4] =  {{1,  2,  3,  10},

                      {4,  5,  6,  11},

                      {7,  8,  9,  12},

                      {13, 14, 15, 16}}

Output:  1 2 4 7 5 3 10 6 8 13 14 9 11 12 15 16

Explanation: Starting from the number 1

then diagonally from above to below that is 2 and 4

then diagonally upward from below that is 7, 5, 3

then diagonally from above to below that is 10 6 8 13

T then diagonally from lower to higher that is 14 9 11

then diagonally from above to below that is 12 15

then it will end at the number 16

reach: As can be seen from the diagram, each piece is written either diagonally or upwards diagonally downward. Print the items diagonally upward starting at index (0,0), then change the orientation, change the column, and print them diagonally downward. Up until the final component is reached, this cycle is repeated.

Algorithm for the approach:

1. Create the variables i=0 and j=0 to hold the current row and column indices.
2. Continually loop between 0 and n*n, in which n is a matrix side.
3. To determine if the orientation is above or downwards, use the flag isUp. The orientation is originally upward when isUp = true.
4. Start printing elements if isUp = 1 by increasing the column index and decreasing the row index.
5. The column index will be decreased and the row index will be increased if isUp = 0.
6. Go to the following row or column (next beginning row and column).
7. Repeat until all elements have been explored.

PrintMatrixInDiagonal.java

// Matrix printing in diagonal order using a Java program
class PrintMatrixInDiagonal  {
    static final int MAX = 100;
    static void printMatrixInDiagonal(int mat[][], int m)
    {
        // Set the following element's indexes to their initial values.
        int s = 0, h = 0;
        // the starting direction is up from down.
        boolean isUpwa = true;
        // until each entry in the matrix has been traversed
        for (int l = 0; l < m * m;) {
           // Traverse from downhill 
         // to upward if isUpwa = true.
            if (isUpwa) {
                for (; s >= 0 && h < m; h++, s--) {
                    System.out.print(mat[i][j] + " ");
                    l++;
                }
                // According to the direction, align s and h.
                if (s < 0 && h <= m - 1)
                    s = 0;
                if (h == m) {
                    s = s + 2;
                    h--;
                }
            }
            // Traverse from up to down if isUpwa = 0.
            else {
                for (; h >= 0 && s < m; s++, h--) {
                    System.out.print(mat[s][h] + " ");
                    l++;
                }
                // According to the direction, align s and h.
                if (h < 0 && s <= m - 1)
                    h = 0;
                if (s == m) {
                    h = h + 2;
                    s--;
                }
            }
            // To alter the direction, revert the isUpwa
            isUpwa = !isUpwa;
        }
    }
    // It is the Driver code
    public static void main(String[] args)
    {
        int mat[][] = { { 1, 2, 3 },
                        { 4, 5, 6 },
                        { 7, 8, 9 } };
        int n = 3;
        printMatrixDiagonal(mat, m);
    }
}

Output:

1  2  4  7  5  3  6  8  9

Alternative Version:

The same strategy as described before is used in this straightforward and condensed implementation.

// Matrix printing in diagonal order using a Java program
public class PrintMatrixInDiagonal {
    public static void main(String[] args)
    {
        // Initializing the matrix
        int[][] mat = { { 1, 2, 3, 4 },
                        { 5, 6, 7, 8 },
                        { 9, 10, 11, 12 },
                        { 13, 14, 15, 16 } };
        // size is taken as m
        // When the iterator count reaches m, 
       // it rises until the mode is switched to derive up
       //down traversal, at which point it reduces.
        int m = 4, type = 0, iti = 0, lower = 0;
 
        // There will be 2m iterations.
        for (int p = 0; p < (2 * m - 1); p++) {
            int p1 = p;
            if (p1 >= m) {
                type++;
                p1 = m - 1;
                iti--;
                lower++;
            }
            else {
                lower = 0;
                iti++;
            }
            for (int s = p1; s >= lower; s--) {
                if ((p1 + type) % 2 == 0) {
                    System.out.println(mat[s][p1 + lower - s]);
                }
                else {
                    System.out.println(mat[p1 + lower - s][s]);
                }
            }
        }
    }
}

Output:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16