Factorial of a Large Number in Java
We've already talked about a number's factorial. We must still go over the factorial of a large number separately, though. The method used to determine the factorial of a small number cannot be used to compute the factorial of a large number. So, we'll talk about how to find a large number’s factorial in Java in this section. Let's use an illustration to help us comprehend.
The factorial of 10 is as follows:
10! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 3628800
The number 3628800 is simple to store. But what if we had to compute the factorial of 110 rather than only 10? The 110 factorial is:
110! = 110 x 109 x 108 x 107 x 106 x … x 3 x 2 x 1 =
15882455415227429404253703127090772871724410234473563207581748318444567162948183030959960131517678520479243672638179990208521148623422266876757623911219200000000000000000000000000
The issue at hand is how to store the factorial of the 110-digit number, which has 179 digits.
The issue at hand is how to store the factorial of the 110-digit number, which has 179 digits.
Here is an example of a simple factorial program using a loop.
Java Program to Find Factorial of a Large Number
Filename: Factorial2.java
class Factorial2{
public static void main(String args[]){
int i,fact=1;
int number=7;//It is the number to calculate factorial
for(i=1;i<=number;i++){
fact=fact*i;
}
System.out.println("Factorial of "+number+" is: "+fact);
}
} Output
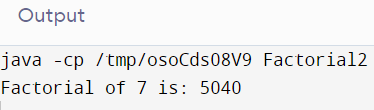
The above-displayed output shows the factorial of the number 7. 7! = 5040.
Here is an example of a simple factorial program using recursion
Let’s see another approach for the same.
Filename: Factoriall.java
class Factoriall{
static int factorial(int n){
if (n == 0)
return 1;
else
return(n * factorial(n-1));
}
public static void main(String args[]){
int i,fact=1;
int number=6;//It is the number to calculate factorial
fact = factorial(number);
System.out.println("Factorial of "+number+" is: "+fact);
}
}
Output
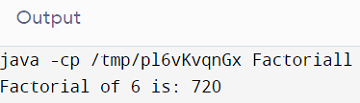
The above-displayed output shows the factorial of the number 6. 6! = 720.
Algorithm
Step 1: Create an array called "result[]" in the first step. The size of the array should be maximum and the maximum is the number of digits present in the output.
Step 2: Set the size of the result[] array resultSize to 1 and the value stored in the array "result[]" to 1.
Step 3: Complete the steps below for each and every number between y = 2 and num.
- To maintain the result of multiplication, multiply y with the result[] and update the result[] and the resultSize.
The algorithm previously discussed emphasizes the use of elementary-level mathematics. In order to multiply two numbers, one digit from each number is chosen, and then the carry is advanced for the subsequent multiplication of two digits. Let's use an illustration to assist you to comprehend it.
Let's say we need to multiply 9786 by 10. The following is how the multiplication will be done after that.
In the array, save the number 9786 as:
result[] = {6, 8, 7, 9}
y = 10
Set the carry to 0 to begin.
Do following for j = 0 to resultSize – 1
- Calculate the value of result[j] * y + v. Let the product be the value.
- Update result[j] by storing the product's last digit in it.
- Update the carry by maintaining the carry's leftover digits.
j = 0, product = result[0] * y + c = 6 * 10 + 0 = 60.
result[0] = 0, c = 6
j = 1, product = result[1] * y + c = 8 * 10 + 6 = 86
result [1] = 6, c = 8
j = 2, product = result[2] * y + c = 7 * 10 + 8 = 78
result [2] = 8, c = 7
j = 3, product = result[3] * y + c = 9 * 10 + 7 = 97
result [3] = 7, c = 9
Now, put all of the digits of carry in result[] and increase resultSize by the number of digits present in carry.
Thus,
result[4] = c = 9
Hence, the result array becomes:
result[] = {0, 6, 8, 7, 9}
Now, all we have to do is to print the result array in reverse order. Thus, 97860 is what we get when we multiply 9786 by 10.
Please keep in mind that we have placed the digits of the number 9786 in reverse order in the result array. It is because storing the digits in the same order as they appear in the number would have made updating the result[] without any extra space problematic.
Implementation
Let's take a look at the algorithm's implementation.
Using Array
An array in Java is an object that includes components of the same data type. Furthermore, array elements are kept in a continuous memory area. It is a data structure in which similar elements are stored. A Java array can only hold a fixed number of entries.
In Java, arrays are index-based; the first element of the array is kept at the 0th index, the second element at the 1st index, and so on.
FileName: Example1.java
public class Example1
{
// assuming that the digits of the factorial of a
// number can not exceed 400.
// If the digits of the output, which is the factorial
// of a large number exceeds 400, then change the
// number accordingly.
int result[] = new int[400] ;
// a method that finds the factorial of
// the large numbers and then
// returns the number of digits present in the factorial
public int factorial(int num)
{
// Initialize the result
result[0] = 1 ;
int resultSize = 1 ;
// Applying the simple formula of factorial
// f! = 1 x 2 x 3 x 4 ... x f
for (int f = 2; f <= num; f++)
{
resultSize = multiply(f, result, resultSize) ;
}
return resultSize ; //return resultSize
}
// The following method multiplies x with the number
// represented by the result[] array. resultSize is the size of the result[] array
// or the number of digits resent in the number that is represented by result[].
// The method uses basic school mathematics for
// the multiplication. The method may increase the value of resultSize
// and returns a new value of the resultSize
static int multiply(int y, int result[], int resultSize)
{
int c = 0; // Initializing the carry
// performing the basic multiplication
// and updating the result array
for (int j = 0; j < resultSize; j++)
{
int product = result[j] * y + c ;
result[j] = product % 10; // Storing the last digit of
// 'product' in the result[] array
c = product / 10 ; // Put the rest in c
}
// Putting the carry in the result[] array and increasing the result size resultSize
while (c != 0)
{
result[resultSize] = c % 10 ;
c = c / 10;
resultSize = resultSize + 1 ;
}
return resultSize;
}
// main method
public static void main(String argvs[])
{
int num = 110 ; //variable num
// creating an object of the class Example1
Example1 obj = new Example1() ;
// storing the result of the method factorial()
int resSize = obj.factorial(num) ; //variable resSize
System.out.println("The factorial of the number " + num + " is: ") ;
// printing the result
for(int j = resSize - 1; j >= 0; j--) //for loop
{
System.out.print(obj.result[j]) ; //printing
}
}
}Output
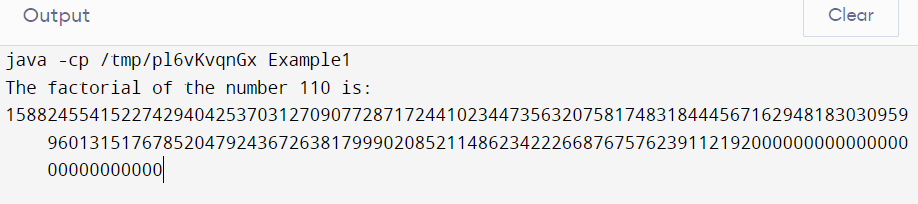
The above-displayed output shows the factorial of the number 110 .
Using LinkedList
To find the factorial of a large integer, a linked list can be used instead of an array. The advantage of utilizing a linked list is that it does not take up any extra space.
The elements are stored in a double-linked list using the Java LinkedList class. It gives you a linked-list data structure. It inherits from AbstractList and implements the List and Deque interfaces.
The following are the most significant aspects of Java LinkedList:
- The LinkedList class in Java might have duplicate elements.
- The LinkedList class in Java maintains insertion order.
- The LinkedList class in Java is not synchronized.
- Manipulation in the Java LinkedList class is quick since no shifting is required.
- The LinkedList class in Java can function as a list, stack, or queue.
FileName: Example2.java
public class Example2
{
// main method
public static void main(String[] args)
{
int num = 110;
// creating an object of the class LargeNumFact1
Example2 obj1 = new Example2();
System.out.println("The factorial of the number " + num + " is: ");
// Create the first node of the linked list
// and its value is 1
LinkedListNode obj = new LinkedListNode(1);
// Running a loop from 2 to num and
// multiplying it with every value coming
// in the iteration of the loop
for(int i = 2; i <= num; i++)
{
obj1.Multiply(obj, i);
}
// displaying the result
obj1.display(obj);
}
void Multiply(LinkedListNode h, int n)
{
// a temp variable for keeping the tail
LinkedListNode temp = h;
LinkedListNode prvNode = h;
int c = 0;
while (temp != null)
{
int val = temp.val * n + c;
// storing the last digit
temp.val = val % 10;
c = val / 10;
prvNode = temp;
// Moving temp by 1 prvNode will
// now denote temp
temp = temp.next;
}
// If carry c is greater than 0,
// then we have to create another node
// for it.
while (c != 0)
{
prvNode.next = new LinkedListNode((int)(c % 10));
c /= 10;
prvNode = prvNode.next;
}
}
void display(LinkedListNode h)
{
// Using the tail recursion
// handling the base case
if (h == null)
{
return;
}
display(h.next);
// recursively printing the
// linked list in the reverse order
System.out.print(h.val);
}
}
// instantiating this class
// will create a node of the linked list
class LinkedListNode
{
int val;
LinkedListNode next;
// constructor of the class LinkedListNode
LinkedListNode(int num)
{
// initializing the fields
this.val = num;
this.next = null;
}
} Output
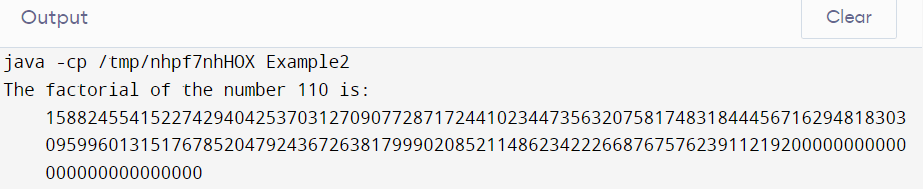
The above-displayed output shows the factorial of the number 110 that is taken as input.
Note: Instead of utilizing tail recursion in the method display(), one might use a loop to traverse over the linked list nodes and then display their data. However, the nodes must be stored on a stack before doing so. This is due to the fact that digits of a number's factorial are stored in reverse order in the linked list. Change the following code in the display() method to get the same result.
public void display1(LinkedListNode h)
{
// creating an object of the class Stack
// Before using the Stack class, use the appropriate import statement for it
Stack<LinkedListNode> stk = new Stack<LinkedListNode>() ;
while(h != null)
{
stk.push(h) ;
h = h.next ;
}
while(stk.isEmpty() == false)
{
LinkedListNode k = stk.pop() ;
System.out.print(k.val) ;
}
}
Using BigInteger
The BigInteger class can also be used to compute the factorial of a large number. The multiply() method offered by the BigInteger class will be used in this approach. Take note of the following code.
For mathematical operations involving extremely large integer calculations that go beyond the capacity of all currently available primitive data types, the BigInteger class is used.
In this way, the BigInteger class is very convenient to use and is frequently used in competitive programming due to its large method library.
FileName: Example3.java
// important import statement
import java.math.BigInteger ;
public class Example3 //class
{
// Returning the Factorial of num
public BigInteger factorial(int num)
{
// Initializing the result
// by instantiating the BigInteger class
BigInteger bi = new BigInteger("1") ;
// Multiplying bi with 2, then 3, then 4, ..., then num
for (int j = 2; j <= num; j++)
{
bi = bi.multiply(BigInteger.valueOf(j)) ;
}
return bi ;
}
// main method
public static void main(String argvs[]) throws Exception
{
int num = 110 ;
// creating an object of the class Example3
Example3 obj = new Example3() ;
// storing the answer
BigInteger bi = obj.factorial(num) ;
System.out.println("The factorial of the number " + num + " is: " + " \n" + bi) ;
}
}
Output
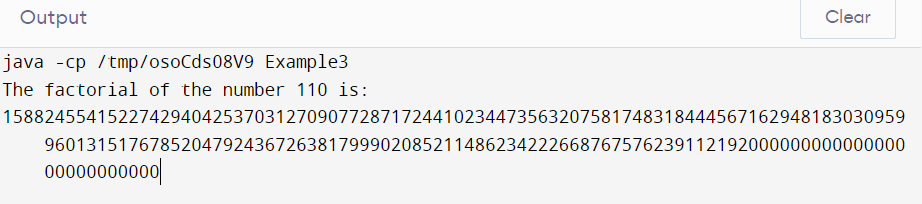
The above-displayed output shows the factorial of the number 110.
The elements are stored in a double-linked list using the Java LinkedList class. It gives you a linked-list data structure. It inherits from AbstractList and implements the List and Deque interfaces.
Program to find the factorial of a large number by taking user input
Filename: Main.java
import java.math.* ;
import java.util.* ;
class Main {
public
static void main(String[] args) {
Scanner input = new Scanner(System.in) ;
long n = input.nextLong() ;
System.out.println(fact(n)) ;
}
public
static BigInteger fact(long n) {
BigInteger result = BigInteger.ONE ;
for (int i = 1; i <= n; i++)
result = result.multiply(BigInteger.valueOf(i)) ;
return result ;
}
}Output
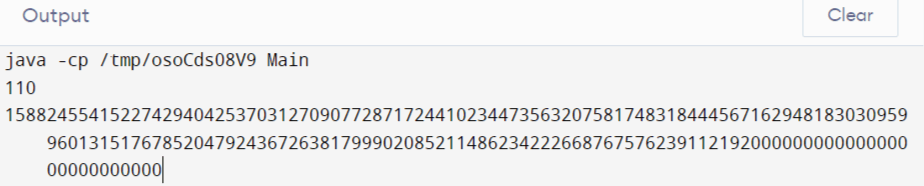
The above-displayed output shows the factorial of the number 110 that is taken as input.