Topological Sort In Java
Topological sort is mainly used in the linear ordering of vertices in a Directed Acyclic Graph (DAG). Topological sort in Java illustrates how to do the linear ordering of vertices in programming. Here linear ordering of vertices means for every two nodes of the directed acyclic graph, v and u, such that v -> u, node v should always come before u.
Algorithm & Pseudo Code
Step I: Create the graph by calling createEdge(‘x’,’y’).
Step II: Call the topologicalSorting( )
- Make a Boolean array (named as visit[ ]) and a stack ;
- b: Populate the ‘false’ value to all the elements of the vist[] array. The ‘false’ value of an element means that the element is not visited.
- Invoke the helping function topologicalSortUtility() recursively to keep track of the Topological Sort beginning from all the vertices one by one.
Step III: Define topologicalSortUtil(char node, bool visit[], stack<Character> &stk):
- Update the Boolean array visit by marking the current node as visited, i.e., ‘true’ value should be added corresponding to the current node.
- Visit all the vertices adjacent to the current vertex by recursively calling the topologicalSortUtility() method. Ensure that recursion only happens when the adjacent vertex is not visited, i.e.,
- In order to store the result, add the current vertex to the stack.
Step IV: In the end, after returning from the helping function, display the contents of the stack.
Java Program
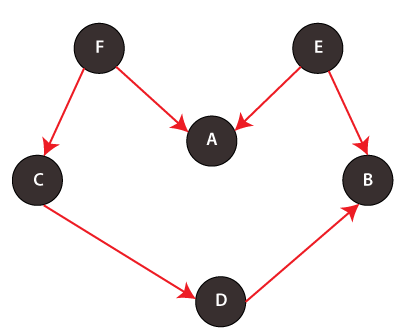
The following code implements Topological sort using the algorithm defined above. The code does the implementation of the following direct acyclic graph.
FileName: TopologicalSortExample.java
Output:
Explanation: The parameterized constructor takes an argument that defines the number of nodes present in the graph. In the constructor, the adjacency list is also created. The createEdge() method updates the adjacency matrix whenever an edge is created between two nodes. The topologicalSortUtility() method uses this adjacency list to traverse through the elements that are adjacent to the current element.
Note that in the above code snippet, the number 65 is used frequently. The number 65 is the ASCII value of the letter ‘A’. Therefore, when (int)‘A’ – 65 is done, internally, ‘A’ gets converted to 65 and 65 – 65 = 0. Therefore, the letter ‘A’ points to the 0th index of the Boolean array visited or 0th row of the adjacency list. Similar logic for the other letters too. For converting numbers to the letter, 65 is added to the number then type casted into chars, i.e., (char)i + 65, where is also a number.
Analysis of the Topological Sort
Topological sort is opposite to the DFS (Depth First Search). In DFS, the farthermost adjacent is visited first, and then we move backward to visit the other nodes, whereas, in topological sort, the current node is visited before its adjacent nodes, which is achieved using a stack. Thus, the topological sort is DFS with the stack.
Time Complexity
Since the topological sort is DFS with stack, the time complexity of the topological sort is equal to the DFS, which is O(V + E), where V is the number of vertices, and E is total number of edges presented in the graph. Similar to DFS, topological sort also has the same best, worst as well as average time complexity, i.e., O(V + E).
Space Complexity
To store and print the nodes of the acyclic graph, a stack is used whose size can’t go beyond the total number of nodes present in the graph. Thus, space complexity is O(n), where n is the total number of elements present in the array. The O(n) space complexity is same for the best, worst as well as average cases.
Conclusion
Topological sort does the sorting on the basis of the ordering of the elements in the graph. For example, in the above graph, node F should always come before node A.
Thus, when there is a requirement that completion of work must be done before the other work, we need a topological sort to do the ordering.
For example, suppose there are two Java files ABC.java, which contains the class ABC{}, and PQR.java. Let’s assume that in the file PQR.java, one is creating an object of the class ABC{}. Therefore, the PQR.java file is dependent on the class ABC{}. Hence, the file ABC.java should be executed first, then the PQR.java.
In such kind of scenario, topological sorting is used. This type of sorting is mainly used in a compiler because a compiler has to decide which file to execute first and which one later.