Keith number in Java
The Keith sequence for a particular Keith number starts with the individual digits of the number, and subsequent terms are generated by summing the digits of the previous terms. The sequence continues until a term is equal to or exceeds the original number. If the last term in the sequence equals the original number, then that number is considered a Keith number.
Example 1:
Input
n = 1537
Output
Yes
Explanation
The number is Keith because it appears in the unique sequence that has first four terms as 1, 5, 3, 7 and remaining terms evaluated using sum of previous 4 terms.
16, 31, 57, 111, 215, 414, 797, 1537.
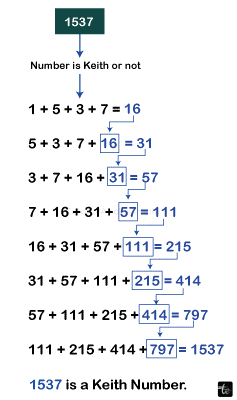
Example 2:
Input
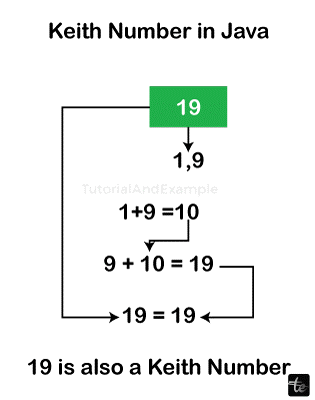
n = 19
Output
Yes
Explanation
The number is Keith because it appears in the unique sequence that has first two terms as 1, 9 and remaining terms evaluated using sum of previous 3 terms.
1, 9, 10, 19.
Approach 1: Iterative Approach
The Iterative Approach for checking if a given number is a Keith number involves simulating the generation of the Keith sequence iteratively until a term equal to or exceeding the original number is reached. This approach uses a loop to repeatedly add the digits of the current terms and update the sequence until the last term matches the original number.
Algorithm
Step 1: Create an ArrayList named digits to store the individual digits of x. Initialize int temp = x to temporarily hold the value of x. Initialize int n = 0 to keep track of the number of digits in x.
Step 2: Extract Digits: Use a loop to extract each digit of x and add it to the digits list. Update temp and n accordingly. Reverse the digits list to get the digits in the correct order (from most significant digit to least significant digit).
Step 3: Generate Keith Sequence: Initialize int nextTerm = 0 to store the next term in the Keith sequence. Initialize int i = n to keep track of the index for generating the next term.
Step 4: Use a while loop to repeatedly generate the next term until it is greater than or equal to x. Inside the loop, set nextTerm to 0. Use a nested loop to sum the previous n terms and update nextTerm. Add the nextTerm to the digits list. Increment i.
Step 5: Check for Keith Number: After the loop, compare nextTerm with the original number x. If nextTerm is equal to x, return true (indicating that x is a Keith number). Otherwise, return false.
Step 6: In the main method, call isKeithNumber with example numbers (14, 19, and 197). Print whether each number is a Keith number or not based on the returned boolean value.
Filename: KeithNumberChecker.java
import java.io.*;
import java.util.*;
public class KeithNumberChecker {
static boolean isKeithNumber(int x) {
// Store all digits of x in a list "digits"
// Also find the number of digits and store in "n".
List<Integer> digits = new ArrayList<>();
int temp = x, n = 0; // n is the number of digits in x
while (temp > 0) {
digits.add(temp % 10);
temp = temp / 10;
n++;
}
// To get digits in the right order (from MSB to LSB)
Collections.reverse(digits);
int nextTerm = 0, i = n;
while (nextTerm < x) {
nextTerm = 0;
// Next term is the sum of previous n terms
for (int j = 1; j <= n; j++)
nextTerm += digits.get(i - j);
digits.add(nextTerm);
i++;
}
return (nextTerm == x);
}
// Driver program
public static void main(String[] args) {
if (isKeithNumber(14))
System.out.println("14 is a Keith number.");
else
System.out.println("14 is not a Keith number.");
if (isKeithNumber(19))
System.out.println("19 is a Keith number.");
else
System.out.println("19 is not a Keith number.");
if (isKeithNumber(197))
System.out.println("197 is a Keith number.");
else
System.out.println("197 is not a Keith number.");
}
}
Output:
14 is a Keith number.
19 is a Keith number.
197 is a Keith number.
Time Complexity
The time complexity of the provided algorithm is O(n^2), where 'n' is the number of digits in the input number 'x'. The primary contributing factor to the time complexity is the nested loop inside the while loop, which sums the previous 'n' terms.
Space Complexity
The space complexity is O(n), where 'n' is the number of digits in the input number 'x'. The algorithm uses an ArrayList named digits to store the individual digits of 'x'. Additionally, other integer variables (e.g., temp, n, nextTerm, i) require constant space.
Approach 2: Brute Force Approach
The Brute-Force Keith Number Search approach involves systematically checking each number within a given range to determine whether it satisfies the properties of a Keith number. A Keith number is a special kind of number where the terms of a particular sequence generated from its digits eventually reach the number itself.
Algorithm
Step 1: Request the user to input the desired number of digits (numLength) for the series.
Step 2: Input Validation: Check if numLength is less than 2. If true, print an error message indicating that the number must have at least 2 digits and exit the program.
Step 3: Calculate the lower and upper bounds (lowerBound and upperBound) for the series using the formula: lowerBound = 10^(numLength - 1) and upperBound = 10^numLength.
Step 4: Iterate through each number num from lowerBound to upperBound - 1. For each num, check whether it is a Keith number using the isKeith method. If true, print num as part of the result.
Step 5: For each number input passed to the isKeith method, initialize the variables: numLength: length of the number, series: an array to keep track of the last three terms, nextTerm: variable to store the next term in the series, number: the original input number. Convert each digit of input into elements of the series array.
Step 6: While nextTerm is less than the original number, calculate the next term in the series based on the sum of the last three terms. Update the series array by shifting elements to the left.
Step 7: If the nextTerm matches the original number, return true. If the loop completes without finding a match, return false. Output all Keith numbers found within the specified range.
Filename: KeithNumberFinder.java
import java.util.Scanner;
public class KeithNumberFinder {
public static void main(String args[]) {
Scanner scanner = new Scanner(System.in);
System.out.print("Enter the number of digits the series must have: ");
// reads an integer as the length of the number from the user
int numLength = scanner.nextInt();
// checks if the length of the number is greater than 2 or not
if (numLength < 2) {
// prints if the above condition returns false
System.out.println("The number must have at least 2 digits.");
} else {
// calculates the lower and upper bounds for the series
long lowerBound = (long) Math.pow(10, numLength - 1);
long upperBound = (long) Math.pow(10, numLength);
for (long num = lowerBound; num < upperBound; num++) {
if (isKeith(String.valueOf(num))) {
// prints all the Keith numbers within the given range
System.out.print(num + ", ");
}
}
}
scanner.close();
}
// function that checks whether the given number is a Keith number or not
public static boolean isKeith(String input) {
int numLength = input.length();
// keep track of only the last three terms
long[] series = new long[numLength];
for (int i = 0; i < numLength; i++) {
series[i] = Long.valueOf(input.substring(i, i + 1));
}
long nextTerm = 0;
long number = Long.valueOf(input);
while (nextTerm < number) {
nextTerm = 0;
// calculates the next term of the series
for (int i = 0; i < numLength; i++) {
nextTerm = nextTerm + series[i];
if (i < numLength - 1) {
// shift the series to the left
series[i] = series[i + 1];
} else {
// add the new value to the series
series[i] = nextTerm;
}
}
// compares the next term of the series with the number and returns a boolean value accordingly
if (nextTerm == number) {
return true;
}
}
return false;
}
}
Output:
Enter the number of digits the series must have: 2
14, 19, 28, 47, 61, 75
Time Complexity
The time complexity of the Brute-Force Keith Number Search algorithm is O(N * M), where N is the size of the range (upperBound - lowerBound) and M is the average number of digits in the numbers within the range. The algorithm iterates through each number within the range and checks its Keith number property, resulting in a linear relationship with the range size and the average number of digits.
Space Complexity
The space complexity is O(M), where M is the number of digits in the input number (num). The algorithm uses a constant amount of space for variables and does not rely on additional data structures that scale with the input size. The primary space usage is associated with the variables used for calculations within the isKeith method.
Conclusion
In conclusion, the Keith Number identification in Java involves determining whether a given number exhibits the Keith property, meaning it is part of a unique sequence generated from its digits.