Insertion Sort in Java

Insertion Sort in Java

Insertion sort in Java is a simple sorting algorithm that works in the same way as we hold cards in hand. Insertion sort does the sorting element-by-element, i.e., take only one element at a time without considering the whole list or array.

The insertion sort virtually divides the array into two halves, one is sorted, and another is un-sorted. Elements from the unsorted part are taken one by one and placed at their proper position in the sorted part. Thus, over a period of time size of sorted part increases and eventually becomes equal to size of the input array or list.

Algorithm

Step 1: Iterate from the second element (arr[1]) to the last element of the array (arr[n-1])

Step 2: Make the comparison of the current element to its predecessors. The comparison should continue till the beginning of the array or till a predecessor element is smaller or equal to the current element.

Step 3: Shift the predecessor elements that are greater than the current element to the right by one position. It is done to make the space positioning the current element to its appropriate location.
Step 4: Shift the current element to its appropriate location.

Pseudo Code

 for (i ? 1; i < size(arr);)
    currentEle ? arr[i]
    j ? i - 1
    while j >= 0 and arr[j] > currentEle
        arr[j + 1] ? arr[j]
        j ? j - 1
    finish while
    arr[j + 1] ? currentEle
    i ? i + 1
end for loop 

Insertion Sort Java Program

The following Java program implements the insertion sort.

FileName: InsertionSortExample.java

 public class InsertionSortExample
{
// method implementing the insertion sort algorithm
static void insertionSort(int a[], int size)
{
    // outer loop iterates over elements of the array
    // starting from the second index and goes till the last index
    for(int i = 1; i < size; i++)
    {
        // j only points the predecessor elements
        int j = i - 1;
        // current element
        int currentEle = a[i];
        // while loop to do the comparison
        // with the  predecessors
        while(j >= 0 && a[j] > currentEle)
        {
            // swapping predecessor elements that
            // are greater than the current element
            a[j + 1] = a[j];
            // checking for other predecessors
            j = j - 1;
        }
        // positioning the current element
        // at its correct position
        a[j + 1] = currentEle;
    }
}
// main method
public static void main(String argvs[])
{
    // given input array
    int a[] = {67, 78, 34, 12, 30, 6, 9, 21};
    // calculating size of the array
    int size = a.length;
    System.out.println("The array before sorting is: ");
    for(int i = 0; i < size; i++)
    {
       System.out.print(a[i] + " ");
    }
    System.out.println("\n") 
    // invoking method insertionSort()
    insertionSort(a, size);
    System.out.println("The array after sorting is: ");
    // displaying the sorted array
    for(int i = 0; i < size; i++)
    {
        System.out.print(a[i] + " ");
    }
}
} 

Output:

 The array before sorting is:
67 78 34 12 30 6 9 21
The array after sorting is:
6 9 12 21 30 34 67 78 

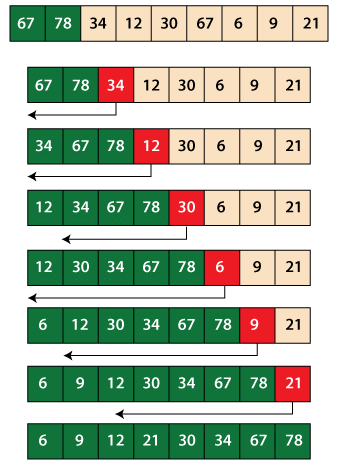
Explanation: In the above program, two pointers approach is used to sort the elements. The outer loop variable i points to the current element whose correct position is to be determined. The inner while loop does the determination of the appropriate position of the current element. At last, the current element is placed at their correct position. The following diagram illustrates the same.

Analysis of the Insertion Sort

Insertion sort is a stable sorting algorithm. However, the insertion sort is not as quick as merge sort or quick sort. Because it usage nested for-loop to do the sorting (see code).

Time Complexity

When a sorted array is provided as the input, the inner while never comes into action, and hence time complexity, which is also the best case for insertion sort, turns out to be O(n), where n is the size of the array. In the average or worst case, the while loop also comes into the picture, and hence time complexity becomes O(n²).

Space Complexity

Similar to bubble sort, insertion sort is also an in-place sorting. The space complexity of the insertion sort is O(1), i.e., constant space for sorting any input array.

Conclusion

Because of the O(n²) time complexity in the average or worst case, the algorithm is not suitable for dealing with large input arrays or lists. If the array is almost sorted and few swaps can make the array sorted, we can go with insertion sort. Also, for arrays of smaller size, insertion sort can be used.