Bubble Sort in Java

Bubble Sort in Java

Bubble sort isalso known as sinking sort. It is one of the simplest sorting algorithms. In the bubble sort algorithm, the given array is traversed from left to right. In this sorting algorithm, adjacent elements are swapped when they are present in the wrong order. Thus, initially, the elements of bigger values are placed at their correct position, then the elements of smaller values. The same phenomenon happens in a water tank too, bubbles of bigger size come out first, then the bubbles of smaller size. Hence, this sorting algorithm is called bubble sort.

Algorithm and Pseudo Code

 start BubbleSort(array)
   for all elements of the input array
      if array[index] > array[index + 1]
         swap(array[index], array[index + 1])
      terminate if
   terminate for
   return array
terminate BubbleSort 

Java Program

The following Java program implements Bubble sort on the basis of pseudo-code written above.

FileName: BubbleSortExample.java

 public class BubbleSortExample
{
// method implementing the bubble sort algorithm
static void bubbleSort(int a[], int start, int end)
{
    // outer loop iterates over elements of the array
    for(int i = start; i < end - 1; i++)
    {
        // inner loop does the swapping of elements that are
        // present in wrong order.
        for(int j = 0; j < end - i - 1; j++)
        {
            if(a[j] > a[j + 1])
            {
                // found that current element
                // is greater than the next element
                // hence do the swapping
                int temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
            }
        }
    }
}
// main method
public static void main(String argvs[])
{
    // given input array
    int a[] = {67, 78, 34, 12, 30, 6, 9, 21};
    // calculating size of the array
    int size = a.length;
    System.out.println("The array before sorting is: ");
    for(int i = 0; i < size; i++)
    {
       System.out.print(a[i] + " ");
    }
    System.out.println("\n");
    // invoking method bubbleSort()
    bubbleSort(a, 0, size);
    System.out.println("The array after sorting is: ");
    // displaying the sorted array
    for(int i = 0; i < size; i++)
    {
        System.out.print(a[i] + " ");
    }
}
} 

Output:

 The array before sorting is:
67 78 34 12 30 6 9 21
The array after sorting is:
6 9 12 21 30 34 67 78 

Explanation: While writing the outer and inner Java for-loop, to implement bubble sort, care must be taken that the exception java.lang.ArrayIndexOutOfBoundsException is not raised in the program. Consider the following taken from the inner for-loop.

for(int i = start; i < end - 1; i++)

lf – 1 is omitted from the condition, the following exception is raised

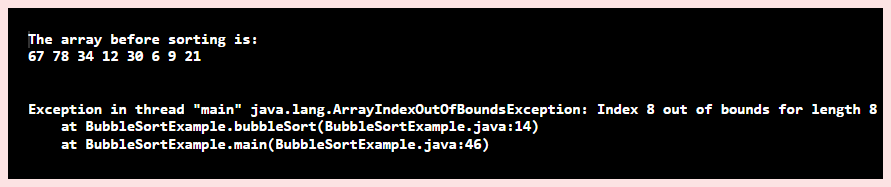
Therefore, while doing the swapping, these aspects must be taken into consideration. The program is very straightforward. The outer loop iterates over array elements, whereas the inner loop ensures elements are present at the proper position. It is the inner loop that does the actual sorting.

Analysis of Bubble Sort

Bubble sort is a simple and stable algorithm. Since the bubble sort uses two nested for-loop, the bubble sort takes more time than the quick or merge sort. The bubble sort uses the comparison of adjacent elements for doing the sorting. Therefore, this sorting algorithm works well for detecting a very small error in computer graphics (like swapping values of two elements).

Time Complexity

On the basis of above-written code, it is evident that bubble sort does not depend on the arrangements of elements. Therefore, the average, best and worst time complexity of the bubble sort is O(n²), where n is the number of elements present in the array. The high time complexity of bubble sort, O(n²), is due to the nesting of two for-loops. Because of high time complexity, this algorithm is not widely used.

The above-written code can be modified to create dependency on the arrangement of elements.

FileName: BubbleSortExample1.java

 public class BubbleSortExample1
{
// method implementing the bubble sort algorithm
static void bubbleSort(int a[], int start, int end)
{
    // outer loop iterates over elements of the array
    for(int i = start; i < end - 1; i++)
    {
        Boolean flag = true;
        // inner loop does the swapping of elements that are
        // present in wrong order.
        for(int j = 0; j < end - i - 1; j++)
        {
            if(a[j] > a[j + 1])
            {
                // found that current element
                // is greater than the next element
                // hence do the swapping
                int temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
                 // swapping has occurred; therefore, iteration of loops should continue.
                flag = false;
            }
        }
        if(flag)
        {
            // the input array is now sorted.
            // Therefore, no need to go further.
            break;
        }
    }
}
// main method
public static void main(String argvs[])
{
    // given input array
    int a[] = {67, 78, 34, 12, 30, 6, 9, 21};
    // calculating size of the array
    int size = a.length;
    System.out.println("The array before sorting is: ");
    for(int i = 0; i < size; i++)
    {
       System.out.print(a[i] + " ");
    }
    System.out.println("\n");
    // invoking method bubbleSort()
    bubbleSort(a, 0, size);
    System.out.println("The array after sorting is: ");
    // displaying the sorted array
    for(int i = 0; i < size; i++)
    {
        System.out.print(a[i] + " ");
    }
}
} 

Output:

 The array before sorting is:
67 78 34 12 30 6 9 21
The array after sorting is:
6 9 12 21 30 34 67 78 

Explanation: The only difference between the previous and the above-written code is the introduction of the flag variable. The flag indicates whether the input array is sorted or not. The flag variable is initialized to the true value, it means the array is sorted. Now, if the inner for-loop finds the wrong order of elements, if block of the inner loop executes, does the swapping of elements and update the value of flag variable from true to false, which means the array is not completely sorted and iteration should continue. If the flag variable retains true even after the execution of the inner loop, the if block after the inner loop executes, and takes the control out of the outer for-loop and thus ruling out the possibility of any further iterations. The following diagram demonstrates the same.

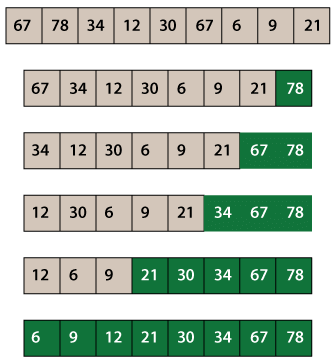
The time complexity of the above-written program is still O(n²) for the average and worst cases. However, for the best case (when a sorted array is taken as input), the time complexity reduces from O(n²) to O(n). If required, the above implementation of the bubble sort is used, not the previous one.

Space Complexity

Similar to the quick sort, the space complexity of the bubble sort algorithm is also O(1), that is, constant space complexity. In the above implementations; there is no auxiliary array or any additional space used to do the sorting.