Matrix Multiplication Program in Java

Matrix Multiplication Program in Java

The matrix multiplication program in Java is the continuation of the matrix program in Java that we have already discussed earlier. In this section, we will learn how to multiply matrices.

To find the multiplication of two matrices, we take elements of the first matrix row-wise and elements of the second matrix column-wise. The steps involved to find the multiplication of matrices is given below.

Step 1: Take two input matrices. Let’s assume the input matrices are:

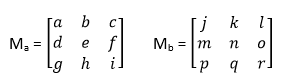
Here, M_a is the first input matrix, and M_b is the second input matrix.

Step 2: Compare the number of columns of the first matrix with the number of rows of the second matrix. It must be equal otherwise multiplication is not possible.

In our case, the number of columns in matrix M_a is 3, and the number of rows in matrix M_b is 3.

Step 3: Now, take elements of the first matrix row-wise and elements of the second matrix column-wise and do the multiplication and then perform the addition to get the element of the resultant matrix. Thus, elements of the first row of matrix M_a get multiplied to elements of the first column of matrix M_b, and elements of the second row get multiplied to the elements of the second column, and so on. Mathematically it can be represented as:

Let’s implement the logic in a Java program.

Filename: MatrixMultiplication.java

 public class MatrixMultiplication
{
public static void main(String argvs[])
{
               // first input matrix
               int[][] arr1 = { { 12, 3, 4 }, { 51, 23, 31 }, { 5, 6, 7 } };
               // second input matrix
               int[][] arr2 = { { 0, 50 }, { 45, 46 }, { 1, 9 } };
               // calculating number of columns of the first matrix
               int colOfArr1 = arr1[0].length;
               // calculating number of rows of the first matrix
               int rowOfArr1 = arr1.length;
               // calculating number of rows of the second matrix
               int rowOfArr2 = arr2.length;
               // calculating number of columns of the second matrix
               int colOfArr2 = arr2[0].length;
               if(colOfArr1 != rowOfArr2)
               {
                               System.out.print("Multiplication of the given matricx is not possible");
               }
                // reaching here means the number of columns of the first matrix
                // is equal to the number of rows of the second matrix.
                // Hence, multiplication of the given matrices are possible
               else 
               {
                     // contains the output matrix
                      int[][] result = new int[rowOfArr1][colOfArr2];
                     // performing multiplication of the input matrices
                     for (int i = 0; i < rowOfArr1; i++) // loop for the rows of the output matrix
                     {
                               // loop for the columns of the output matrix
                               for (int j = 0; j < colOfArr2; j++)
                               {
                                              // for storing output of every element of the output matrix
                                              int sum = 0;
                                              for (int k = 0; k < colOfArr1; k++)
                                              {
                                                             // taking elements row-wise for the first input matrix
                                                              //and column-wise for the second
                                                             // input matrix
                                                              sum = sum + ( arr1[i][k] * arr2[k][j] );           
                                              }
                                              // updating our result matrix
                                              result[i][j] = sum;
                               }
                     }
                     // Displaying the outcome
                    System.out.println("Multiplication of the given two matrices is: ");
                     for(int row = 0; row < rowOfArr1; row++)
                     {
                                              for (int col = 0; col < colOfArr2; col++)
                                              {
                                                             System.out.print(result[row][col] + " ");
                                              }
                                              System.out.println("");
                     }
               }    
}
} 

Output:

 Multiplication of the given two matrices is:
139 774
1066 3887
277 589 

Explanation: We are nesting Java for-loop to the third degree to achieve our result. The innermost loop handles the multiplication process by taking elements row-wise for the first input array and column-wise for the second input array. We observe that in the given matrix the number of columns of the first matrix is equal to the number of rows of the second matrix.

The multiplication of two matrices is also a matrix whose row size is equal to the row size of the first matrix, and the column size is the same as the column size of the second matrix.

Mathematically, if M_a is an r1 * r2 matrix, and M_b is an r2 * c2 matrix. Then, M_a * M_b = r1 * c2 matrix. Here, r1 and r2 are the row size and column size of the matrix M_a, whereas r2 and c2 are the row size and column size of the matrix M_b.