Merge Two Sorted Arrays without Extra Space in Java
We are going to learn how to merge two already sorted arrays without using extra space.
Problem Statement
The user is provided with two sorted integer arrays in increasing order. The goal is to merge both arrays and display the new array in increasing order.
The constraint is not to use any additional space to accomplish the stated task. In other words, the space complexity of the program should remain constant.
Let us see certain examples to understand the topic in a better way.
Example 1:
Input
int array1[] = {23, 45, 67, 89, 90}
int array2[] = {13, 35, 72, 81, 98}
Output
{13, 23, 35, 45, 67, 72, 81, 89, 90, 98}
Explanation:
On merging the two arrays, the above output is received.
Example 2:
Input
int array1[] = {-23, 45, -67, 89, -90}
int array2[] = {13, 35, -72, 81, 98}
Output
{-90, -72, -67, -23, 13, 35, 45, 81, 89, 98}
Explanation:
On merging the two arrays, the above output is received.
Approach 1: Brute Force and Sorting
It is prohibited to use additional space so, we will put the first m smallest elements in the first input array, while the rest of the len2 elements are in the second input array. Sort the second array, since the first will be already sorted in this process. Further, by using a for-loop display each element is available in both arrays.
It is to be noted that here len1 = size of the first input array and len2 = size of the second input array.
Implementation:
File name: MergeArray.java
import java.util.Arrays;
public class MergeArray {
// defining a method to merge two sorted arrays Arr1 and Arr2 without using any extra space
public void merge_SortedArray(int Arr1[], int Arr2[]) {
// calculating the size of the input arrays
int len1 = Arr1.length;
int len2 = Arr2.length;
// Traversing over the input arrays
// and storing the first a1 smallest element
// in the input array Arr1.
for(int j = 0; j < len1; j++) {
int flag = j;
int min = Arr1[j];
// Calculating the smallest among the remaining elements of 'Arr1'.
for(int k = j; k < len1; k++) {
if(Arr1[k] < min) {
min = Arr1[k];
flag = k;
}
}
// Calculating the smallest among the remaining elements of 'Arr2'.
for(int i = 0; i < len2; i++) {
if(Arr2[i] < min) {
min = Arr2[i];
flag = i;
}
}
// Swapping 'Arr1[j]' with the minimum element.
if(flag < len1 && flag >= j && Arr1[flag] == min) {
swap(Arr1, Arr1, j, flag);
}
else {
swap(Arr1, Arr2, j, flag);
}
}
// Sorting the array 'inArr2'.
Arrays.sort(Arr2);
}
// method for swapping two integers 'a1' and 'a2'.
public static void swap(int Arr1[], int Arr2[], int a1, int a2) {
int tmp = Arr1[a1];
Arr1[a1] = Arr2[a2];
Arr2[a2] = tmp;
}
// main method
public static void main(String argvs[]) {
// creating an object of the class MergeSortedArr
MergeArray obj = new MergeArray();
// input arrays
int Arr1[] = {27, 31, 45, 57, 167, 190, 199, 230};
int Arr2[] = {34, 35, 48, 51, 54, 76, 88, 99};
int len1 = Arr1.length; // calculating size of the first input array
int len2 = Arr2.length; // calculating size of the second input array
System.out.println("The input arrays are: ");
for(int i = 0 ; i < len1; i++) {
System.out.print(Arr1[i] + " ");
}
System.out.println( );
for(int i = 0 ; i < len2; i++) {
System.out.print(Arr2[i] + " ");
}
System.out.println();
// invoking the method merge_SortedArray() for merging the
// array without using any extra space
obj.merge_SortedArray(Arr1, Arr2);
System.out.println( );
System.out.println(" \n Merged Array: ");
for(int i = 0 ; i < len1; i++) {
System.out.print(Arr1[i] + " ");
}
for(int i = 0 ; i < len2; i++) {
System.out.print(Arr2[i] + " ");
}
System.out.println("\n");
}
}
Output:

Complexity Analysis:
Time Complexity: The time complexity of this program is O(n^2) where n is the total number of elements in both arrays. The program iterates over Arr1 n times, and for each iteration, it searches for the smallest element in both Arr1 and Arr2, which takes O(n) time. Additionally, it performs sorting on Arr2 using Arrays.sort(), which takes O(nlogn) time. Therefore, the overall time complexity is O(n^2 + nlogn), which can be transformed into O(n^2) as it is the dominating term.
Space Complexity: The space complexity of this program is O (1), as it uses only a few constant size variables and does not create any additional data structures.
Approach 2: Using Two Pointers and Sorting
We will keep the 'l1' smallest numbers in 'Arr1[]' (which may or may not be sorted) and the remaining elements in 'Arr2[]' (may or may not be sorted). With the help of two pointers, 'p' = 0 and 'q' = 0, we iterate over 'Arr1[]' and 'Arr2[]'. If 'Arr1[p]' is greater than or equal to 2, we swap some 'kth' element of 'Arr1[]' with 'Arr2[q]' and increment 'q'; otherwise, we increment 'p'. It makes sense to replace the major components of 'Arr1[]'. As a result, we set 'k' = 'l1 - 1'. Following that, we decrease 'k' after each switch. Finally, we sort 'Arr1[]' and 'Arr2[]'.
Implementation:
File name: MergeSortedArray2.java
// importing Array package for sorting
import java.util.Arrays;
public class MergeSortedArray2 {
// a method to merge two sorted arrays Arr1 and Arr2 without using any extra space
public void mergeTwoSortedArray(int Arr1[], int Arr2[]) {
int l1 = Arr1.length;
int l2 = Arr2.length;
int p = 0;
int q = 0;
int k = l1 - 1;
// Traversing over the elements of 'Arr1[]' and 'Arr2[]'.
while(q <= k && q < l2) {
if(Arr1[p] < Arr2[q]) {
p = p + 1;
} else {
// Swapping the current elements of 'Arr2[]'
// with the 'kth' element of 'Arr1[]'.
swap(Arr1, Arr2, k, q);
q = q + 1;
k = k - 1;
}
}
// Sorting the array 'Arr1'.
Arrays.sort(Arr1);
// Sorting the array 'Arr2'.
Arrays.sort(Arr2);
}
// method to swap two integers 'a1' and 'a2'.
public static void swap(int Arr1[], int Arr2[], int a1, int a2) {
int tmp = Arr1[a1];
Arr1[a1] = Arr2[a2];
Arr2[a2] = tmp;
}
// main method
public static void main(String argvs[]) {
// creation of an object of the class MergeSortedArray2
MergeSortedArray2 obj = new MergeSortedArray2();
// input arrays
int Arr1[] = {42, 48, 57, 70, 85, 100};
int Arr2[] = {18, 25, 58, 61, 84, 88, 98};
int len1 = Arr1.length; // calculating the length of the first input array
int len2 = Arr2.length; // calculating the length of the second input array
System.out.println("The input arrays are: ");
for(int i = 0 ; i < len1; i++) {
System.out.print(Arr1[i] + " ");
}
System.out.println( );
for(int i = 0 ; i < len2; i++) {
System.out.print(Arr2[i] + " ");
}
// invoking the method mergeTwoSortedArray() to merge the
// array without using any extra space
obj.mergeTwoSortedArray(Arr1, Arr2);
System.out.println( );
System.out.println(" The Merged Array: ");
for(int i = 0 ; i < len1; i++) {
System.out.print(Arr1[i] + " ");
}
for(int i = 0 ; i < len2; i++) {
System.out.print(Arr2[i] + " ");
}
System.out.println( "\n" );
}
}Output:

Complexity Analysis:
Time complexity – The time complexity of the mergeTwoSortedArray method is O(n log n), where n is the total number of elements in both input arrays.
The while loop inside the method runs for a maximum of n iterations. Within the loop, the swap method and the Arrays.sort method both have a time complexity of O(log n), so the overall time complexity of the loop is O(n log n).
The Arrays.sort method is called twice on two different arrays, each with n/2 elements, so the time complexity of those two calls combined is O(n log n).
Therefore, the overall time complexity of the mergeTwoSortedArray method is
O (n log n).
Space complexity - The space complexity is O (1) since the arrays are merged without using any extra space.
Approach 3: Using Euclid's Division Lemma
In this approach, we will perform the swaps in such a way that the arrays are not sorted at the end. We will fill the smallest numbers in the smallest positions rather than the last positions as in Approach 2 (i.e., we will begin with 'k' = 0 rather than 'k' ='l1 - 1'). However, it is possible that a number from 'Arr1[]' is being replaced by some of the numbers from the second array 'Arr2[]' in this case. However, there is a good chance that it will be used at a later point in 'Arr1[]'. As a result, it is necessary to extract the number that was initially positioned at position 'k' in case it was replaced previously.
In this approach, we can use Euclid's Lemma in the following way:
From a number M = X * R + P, we can get 'X' by using simple mathematics i.e., dividing 'M' by 'R' and 'P' by taking the modulus of 'M' by 'R'.
We choose 'MAX' = 10^9 + 1 as 'R' for the complete array 'Arr1[]'.
Implementation:
File name: MergeSortedArr3.java
public class MergeSortedArr3 {
// a method to merge two sorted arrays Arr1 and Arr2 without using any extra space
public void mergeTwoSortedArray(long Arr1[], long Arr2[]) {
// calculation of the length of the input arrays
int len1 = Arr1.length;
int len2 = Arr2.length;
int m = 0;
int q = 0;
int k = 0;
// Maximum element to be used for Euclid's Lemma.
long MAX = 1000000007;
// Traversing over the elements of 'Arr1' and 'Arr2'.
while(m < len1 && q < len2 && k < len1 + len2) {
// Extracting the original numbers.
long orgNum1 = Arr1[m] % MAX;
long orgNum2 = Arr2[q] % MAX;
// Comparing the original numbers.
if(orgNum1 <= orgNum2) {
if(k < len1) {
Arr1[k] = Arr1[k] + (orgNum1 * MAX);
} else {
Arr2[k - len1] = Arr2[k - len1] + (orgNum1 * MAX);
}
m = m + 1;
k = k + 1;
} else {
if(k < len1) {
Arr1[k] = Arr1[k] + (orgNum2 * MAX);
} else {
Arr2[k - len1] = Arr2[k - len1] + (orgNum2 * MAX);
}
q = q + 1;
k = k + 1;
}
}
// Traversing over the remaining elements.
while(q < len2) {
long orgNum2 = Arr2[q] % MAX;
if(k < len1) {
Arr1[k] = Arr1[k] + (orgNum2 * MAX);
} else {
Arr2[k - len1] = Arr2[k - len1] + (orgNum2 * MAX);
}
q = q + 1;
k = k + 1;
}
// Traversing over the rest of the elements of 'Arr1[]'
while(m < len1) {
long orgNum1 = Arr1[m] % MAX;
if(k < len1) {
Arr1[k] = Arr1[k] + (orgNum1 * MAX);
} else {
Arr2[k - len1] = Arr2[k - len1] + (orgNum1 * MAX);
}
m = m + 1;
k = k + 1;
}
// Changing the elements present in the array 'Arr1[]' to the new numbers.
for(int l = 0; l < len1; ++l) {
Arr1[l] = Arr1[l] / MAX;
}
// Changing the elements present in the array 'Arr2[]' to the new numbers.
for(int l = 0; l < len2; ++l) {
Arr2[l] = Arr2[l] / MAX;
}
}
// main method
public static void main(String argvs[]) {
// creation of an object of the class MergeSortedArr2
MergeSortedArr3 obj = new MergeSortedArr3();
// input arrays
long Arr1[] = {1, 3, 7, 9, 15, 20};
long Arr2[] = {2, 5, 8, 11, 14, 16, 18, 19};
int len1 = Arr1.length; // calculating size of the first input array
int len2 = Arr2.length; // calculating the size of the second input array
System.out.println("The input arrays are: ");
for(int i = 0 ; i < len1; i++) {
System.out.print(Arr1[i] + " ");
}
System.out.println( );
for(int i = 0 ; i < len2; i++) {
System.out.print(Arr2[i] + " ");
}
// invoking the method mergeTwoSortedArrray() to merge the
// array without using any extra space
obj.mergeTwoSortedArray(Arr1, Arr2);
System.out.println( );
System.out.println("The merged Array: ");
for(int i = 0 ; i < len1; i++) {
System.out.print(Arr1[i] + " ");
}
for(int i = 0 ; i < len2; i++) {
System.out.print(Arr2[i] + " ");
}
}
}
Output:
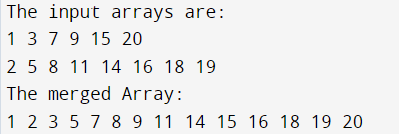
Complexity Analysis:
The time complexity of the mergeTwoSortedArrray()method is O(len1 + len2) where len1 and len2 are the lengths of the input arrays Arr1 and Arr2 respectively.
Conclusion:
The article threw light on how to merge two sorted arrays without using extra space and display the final array in increasing order. Three different approaches were discussed. The last one which is Euclid’s Division Lemma is considered the best due to the least time complexity among the three.