Minimum Cost Path Problem in Java
Introduction:
The Minimum Cost Path problem is an algorithmic problem that involves finding the path with the lowest cost between two points in a given matrix.
To begin with, let us define the problem statement. We are given a matrix M of dimensions m x n, where each cell (i,j) of the matrix has a non-negative integer value representing the cost of traversing that cell. Our task is to find the path with the lowest cost from a starting cell (i1,j1) to an ending cell (i2,j2) in the matrix, where a path is a sequence of cells such that adjacent cells in the sequence are either vertically or horizontally adjacent in the matrix.
Let us take a matrix as a example:
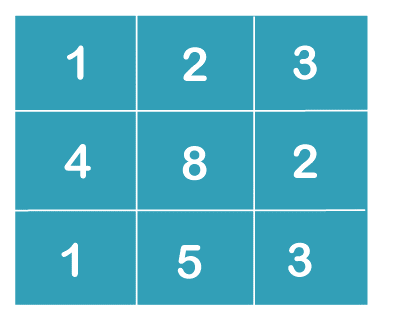
To find the minimum cost path from the top-left corner to the bottom-right corner, we can follow the steps below:
Step 1: Create a new matrix called "cost" of the same size as the input matrix, initialized to all 0s.
Step 2: Initialize cost[0][0] to the value of the first cell in the input matrix.
Step 3: Initialize the first row of cost by adding the value of the current cell in the input matrix to the value of the previous cell in the row of cost.
Step 4: Similarly, initialize the first column of cost by adding the value of the current cell in the input matrix to the value of the previous cell in the column of cost.
Step 5: For each cell in the remaining rows and columns of cost, compute the minimum cost of reaching that cell by comparing the cost of coming from the cell to the left and the cost of coming from the cell above. In other words, cost[i][j] = input[i][j] + min(cost[i-1][j], cost[i][j-1]).
the resulting cost matrix will be:
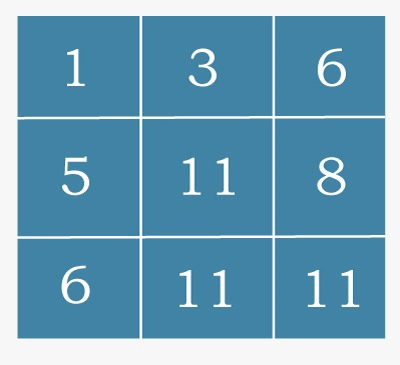
Minimum cost: 11
Minimum cost path: 3 2 3 2 1
Program:
File Name: MinimumCostPath.java:
import java.util.*;
public class MinimumCostPath {
public static void main(String[] args) {
// Define the input matrix
int[][] input = {{1, 2, 3}, {4, 8, 2}, {1, 5, 3}};
// Get the number of rows and columns in the input matrix
int rows = input.length;
int cols = input[0].length;
// Define the cost matrix, which will hold the minimum cost to reach each cell
int[][] cost = new int[rows][cols];
// Initialize the cost of the top-left cell to be the same as the input matrix
cost[0][0] = input[0][0];
// Initialize the cost of the cells in the first row and first column
for (int i = 1; i < rows; i++) {
cost[i][0] = input[i][0] + cost[i-1][0];
}
for (int j = 1; j < cols; j++) {
cost[0][j] = input[0][j] + cost[0][j-1];
}
// Fill the remaining cells in the cost matrix
for (int i = 1; i < rows; i++) {
for (int j = 1; j < cols; j++) {
// The cost of each cell is the sum of the value in the input matrix and the minimum cost
// of the cells directly above and to the left of it
cost[i][j] = input[i][j] + Math.min(cost[i-1][j], cost[i][j-1]);
}
}
// Print the input matrix
System.out.println("Input matrix:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
System.out.print(input[i][j] + " ");
}
System.out.println();
}
// Print the cost matrix
System.out.println("Cost matrix:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
System.out.print(cost[i][j] + " ");
}
System.out.println();
}
// Print the minimum cost and the minimum cost path
System.out.println("Minimum cost: " + cost[rows-1][cols-1]);
System.out.print("Minimum cost path: ");
int i = rows-1;
int j = cols-1;
System.out.print(input[i][j] + " ");
while (i > 0 || j > 0) {
// Starting from the bottom-right cell, backtrack to the top-left cell by following the path
// of minimum cost
if (i == 0) {
j--;
} else if (j == 0) {
i--;
} else if (cost[i-1][j] < cost[i][j-1]) {
i--;
} else {
j--;
}
System.out.print(input[i][j] + " ");
}
}
}Output:
java -cp /tmp/MmIh5FGFrI MinimumCostPath
Input matrix:
1 2 3
4 8 2
1 5 3
Cost matrix:
1 3 6
5 11 8
6 11 11
Minimum cost: 11
Minimum cost path: 3 2 3 2 1
Complexity Analysis:
The time complexity of the minimum cost path algorithm using dynamic programming is O(mn), where m is the number of rows in the input matrix and n is the number of columns. The algorithm iterates over every cell in the matrix exactly once.
The space complexity is also O(mn) because the algorithm uses an additional matrix of the same size to store the intermediate results. Therefore, the space required by the algorithm is proportional to the size of the input matrix.
Approach 2: using Recursion
The minimum cost path problem can also be solved using a recursive approach. The basic idea is to find the minimum cost to reach the bottom-right cell from the current cell by recursively finding the minimum cost from the adjacent cells (i.e., left, right, top, and bottom cells).
Program:
FileName: MinimumCostPath.java
import java.util.*;
public class MinimumCostPath {
public static int minCost(int[][] input, int i, int j) {
// If the current cell is the bottom-right cell, return the cost of the cell
if (i == input.length - 1 && j == input[0].length - 1) {
return input[i][j];
}
// If the current cell is the last row, add the cost of the right cell and recurse
if (i == input.length - 1) {
return input[i][j] + minCost(input, i, j+1);
}
// If the current cell is the last column, add the cost of the bottom cell and recurse
if (j == input[0].length - 1) {
return input[i][j] + minCost(input, i+1, j);
}
// Find the minimum cost to reach the bottom-right cell from the adjacent cells and add the cost of the current cell
int right = minCost(input, i, j+1);
int bottom = minCost(input, i+1, j);
return input[i][j] + Math.min(right, bottom);
}
public static void main(String[] args) {
int[][] input = {{1, 2, 3}, {4, 8, 2}, {1, 5, 3}};
int minCost = minCost(input, 0, 0);
System.out.println("Minimum cost: " + minCost);
}
}Output:
Minimum cost: 11
Explanation:
The minimum cost path from the top-left cell to the bottom-right cell of the input matrix {{1, 2, 3}, {4, 8, 2}, {1, 5, 3}} is 11, which corresponds to the path 3->2->3->2->1. The minCost method recursively computes the minimum cost of reaching the bottom-right cell from the current cell to get the minimum cost of the entire path.
Complexity Analysis:
The time complexity of the recursive approach is O(2^(m+n)), where m and n are the number of rows and columns in the input matrix. Because in the worst case, we need to explore all possible paths from the top-left cell to the bottom-right cell, and the number of such paths is 2^(m+n).
The space complexity of the recursive approach is O(m+n), which is the maximum depth of the recursive call stack. Here at any given point, we only need to keep track of the current cell, and the depth of the call stack is equal to the number of cells in the longest path from the top-left cell to the bottom-right cell.