Selection Sort in Java

Selection Sort in Java

Selection sort is also a simple sorting algorithm that works by repeatedly finding the minimum element from the unsorted portion of the input array, and placing it in the sorted portion of the array. Thus, selection sort maintains two subarrays, one is sorted and another one is not sorted. In every iteration, the size of the sorted subarray increases, and the size of the unsorted subarray decreases.

Algorithm and Pseudo Code

 selectionSort(arr, size)
 for( int i -> 0 to (size - 1) times )
  Assume that the first element encountered in each iteration, arr[i], as the current minimum element.
Store the index of the current minimum element, say minIndex
   for( int j -> i + 1 to size times)
    if arr[j] < arr[minIndex]
      update the minIndex as j
     end if
   end for
  swap the value present at the minIndex with first unsorted position, i.e, arr[i]
 end for
end selectionSort 

Selection Sort Java Program

The following Java program implements the selection sort algorithm.

FileName: SelectionSortExample.java

 public class SelectionSortExample
{
// method implementing the selection sort algorithm
static void selectionSort(int a[], int size)
{
    // outer loop iterates over elements of the array
    // starting from the first index and goes till the second last index
    for(int i = 0; i < size - 1; i++)
    {
        // assuming the first element of every iteration is
        // the minimum element and hence storing its index
        int minIndex = i;
        // iterating over elements starting from next to minIndex
        for(int j = i + 1; j < size; j++)
        {
            if(a[minIndex] > a[j])
            {
                // a[j] is smaller than the value
                // present at the minIndex.
                // Hence, updating the minIndex
                minIndex = j;
            }
        }
        // positioninig the element found
        // at the minIndex to its appropriate position
        int temp = a[minIndex];
        a[minIndex] = a[i];
        a[i] = temp;
    }
}
// main method
public static void main(String argvs[])
{
    // given input array
    int a[] = {67, 78, 34, 12, 30, 6, 9, 21};
    // calculating size of the array
    int size = a.length;
    System.out.println("The array before sorting is: ");
    for(int i = 0; i < size; i++)
    {
       System.out.print(a[i] + " ");
    }
    System.out.println("\n");
    // invoking method selectionSort()
    selectionSort(a, size);
    System.out.println("The array after sorting is: ");
    // displaying the sorted array
    for(int i = 0; i < size; i++)
    {
        System.out.print(a[i] + " ");
    }
}
} 

Output:

 The array before sorting is:
67 78 34 12 30 6 9 21
The array after sorting is:
6 9 12 21 30 34 67 78 

Explanation: In the above program, the first iteration of the outer loop finds the minimum element of the array, and the minimum element is placed at the first index, i.e., the 0^th index, the second iteration of the outer loop finds the second minimum element of the array and puts the second minimum at the 1^st index, the third iteration find the third minimum, places it on the 2^nd index and so on for rest of the iteration. Thus, virtually dividing the array into the sorted and unsorted parts. The following diagram depicts the same.

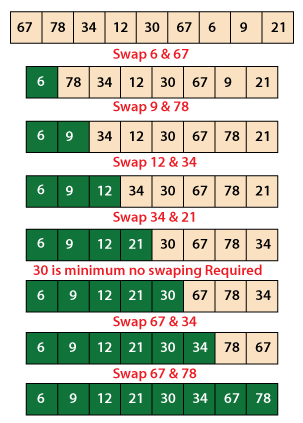
It is the inner for-loop that does the searching of minimum elements. The outer loop tells the inner loop from where it should start the search of minimum element.

Analysis of the Selection Sort

If we observe, we find that selection sort is nothing but the reverse process of bubble sort. In bubble sort every, every iteration finds the maximum elements of the array and places those maximum elements at the rightmost side. In selection sort, every iteration finds the minimum elements of the array and places those minimum elements at the leftmost side. Thus, the behavior of the selection sort is almost similar to the selection sort.  The good thing about selection sort is it never makes more than n swaps to do the sorting, where n is the size of the array or list.

Time Complexity

Selection sort never cares about the arrangement of elements, i.e., even if a sorted array is provided as the input, the selection sort goes on to find the minimum element for the sorted array. Because of the nesting of two for loops, the time complexity of the selection sort is O(n^2), where n is the number of elements present in the list/ array. Since this sorting algorithm is independent of element arrangements, the best, average, or in the worst case, the time complexity remains the same, i.e., O(n^2).

Space Complexity

The selection sort does the in-place sorting. Therefore, the space complexity for the selection sort turns out to be O(1), i.e., constant space for sorting the input array or list.

Conclusion

Similar to bubble sort, this sorting algorithm should not be used for large lists or arrays because of the time complexity O(n^2). For a small list, one can go with the selection sort.