Python Maurer Rose and Rhodonea Curves

In this tutorial, in Python we will make a Maurer Rose example and Rhodonea Curve example. Before we continue to see what precisely is maurer rose or a rhodonea bend we really want to get the fundamental construction of our program prepared.

Rhodonea Curve

In science, a rose or rhodonea bend is a sinusoid indicated by either the cosine or sine capacities with no stage point that is plotted in polar directions. Rose bends or "rhodonea" are named by the mathematician of Italian, between the years 1748 and 1743, who concentrated, Guido Grandi.

• In light of its blossom like structure, the rhodonea (bend) is likewise called the rosette or the rose.
• The amplitude of the two term of the boundary’s conditions is equivalent because it is a hypocycloid.
• The quantity of petals is the denominator of: 1 / 4 – 1 / (4 c).
• For unreasonable c the bend doesn't close, and the quantity of petals is boundless. For sane c, the subsequent bend is logarithmic.
• Model: for c = 5 / 4 the quantity of petals is 15

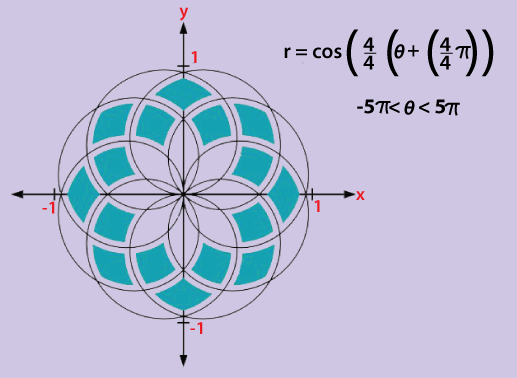
A few associations with different bends:

• It is the polar opposite of the epi twisting, the conchoid of the bend is the botanic bend.
• It is likewise the pedals of the hypocycloid.
• The rhodonea curve is the outspread and the pedals of the epicycloid

To code for rhodonea curves and maurer rose we need to learn about degrees and radians Demonstrating radians ()

To demonstrate working of radians ()

Below is the Source code:

# Python code to exhibit working of radians () for radians
# Printing radians counterparts.
import math
print ("The 180 value/pi value Degrees is equal to Radians =: ", end =" ")
print (math.radians (180 / math.pi))




print ("The 180 value Degrees is of Radians =: ", end =" ")
print (math.radians (180))




print ("The one Degrees is of Radians =: ", end =" ")
print (math.radians (1))

Output:

The 180value / pi value Degrees is of Radians = 1.0
The 180 value Degrees is of Radians = 3.145467594653589793
The one Degrees is of Radians = 0.01745346579919943495

Demonstrating degrees ()

This capacity acknowledges the "radians" as information and converts it into its certificates same.

Python code to show working of degrees () for degrees (), Printing degrees reciprocals.

Below is the Source code:

import math




print ("The pi value / 180 value Radians is of Degrees: ", end = " ")
print (math.degrees (math.pi / 180))




print ("The 180 value Radians is of Degrees: ", end = " ")
print (math.degrees (180))




print ("The 1 value Radians is of Degrees: ", end = " ")
print (math.degrees (1))

Output:

The pi value /180 value Radians is of Degrees: 1.0
The 180 value Radians is of Degrees: 15313.4406643314354817
The 1 value Radians is of Degrees: 57.49577646951308434

There are numerous potential uses of these capacities in numerical calculations connected with math and has a specific applications in galactic calculations also.

Program’s Basic Structure -

Approach to begin with the code, Steps-by-step method:

 we continue on to learn anything about Rhodonea bends or Maurer rose examples, we first need to get the essential construction of our program prepared. With the goal that when we refactor our code we will just adjust a capacity while the remainder of the program will be something similar. So here's the fundamental construction of the program -

Step 1: import required modules

import pygame
from math import cos
from math import sin
from math import radians

also set our program variables width1 and height1 respectively

(width1, height1) = (850, 650)

Step 2: init the screen surface and Setting up the window

Screen1 = pygame.display.set_mode ( (width1, height1))
pygame.display.set_caption ('Rose Curve in Python !')

Step 3:  the screen background color

screen.fill ( (450, 450, 405)) 

Step 4: to draw the rosey pattern, our function is defined

drawPattern1 ()

Step 5:  Flip the drawn material with the recently made material (twofold buffering)

Below is the part of Source code (not meant for execution alone):

def run_demo (width1, height1, fps):
      pygame.init ()
       screen = pygame.display.set_mode ( (width1, height1))
       pygame.display.set_caption ('press space to see next demo')
       background = create_background (width1, height1)
clock = pygame.time.Clock ()
demo = [ do_rectanglular shape_demo,
do_circle_demo,
do_horrible_outlines,
do_nice_outlines,
do_polygon_demo,
do_line_demo  ]
the_world_is_a_happy_place = 0
while True:
the_world_is_a_happy_place + = 1
for event in pygame.event.get ():
if is_trying_to_quit (event):
return
if event.type = = pygame.KEYDOWN and event.key = = pygame.K_SPACE:
demo = demo [1:]
screen.blit (background,  (0, 0))
if len (demo) = = 0:
return
demo [0] (screen, the_world_is_a_happy_place)
pygame.display.flip ()
clock.tick (fps)

Step 6:  Basically, we're reviving the screen surface subsequent to drawing

pygame.display.flip ()

Step 7: main logic

Poll the occasions in the eventline

deactivating pygame and quitting the program, if the client shutting the window

Drawing the surface item to the console screen.

while True:
for event in pygame.event.get ():
if event.type = = pygame.QUIT :
pygame.quit ()
quit ()
pygame.display.update ()

Code snippet: This shows basically the combined code of above steps.

from math import sin
from math import cos
from math import radians
import pygame
 (width1, height1) = (850, 650)
screen = pygame.display.set_mode ((width1, height1))




pygame.display.set_caption ('Rose Curve in Python!')




screen.fill ( (450, 450, 405)) # lemonChiffon color
drawPattern1 ()
pygame.display.flip ()
def run_demo (width1, height1, fps):
        pygame.init ()
        screen = pygame.display.set_mode ( (width1, height1))
        pygame.display.set_caption ('press space to see next demo')
        background = create_background (width1, height1)
        clock = pygame.time.Clock ()
        demo = [
                do_rectanglular shape_demo,
                do_circle_demo,
                do_horrible_outlines,
                do_nice_outlines,
                do_polygon_demo,
                do_line_demo  ]
        the_world_is_a_happy_place = 0
        while True:
                the_world_is_a_happy_place + = 1
                for event in pygame.event.get ():
                        if is_trying_to_quit (event):
                                return
                        if event.type = = pygame.KEYDOWN and event.key = = pygame.K_SPACE:
                                demo = demo [1:]
                screen.blit (background,  (0, 0))
                if len (demo) = = 0:
                        return
                demo [0] (screen, the_world_is_a_happy_place)
                pygame.display.flip ()
                clock.tick (fps)




while True:


for event in pygame.event.get ():




if event.type = = pygame.QUIT :




pygame.quit ()
quit ()




pygame.display.update ()

Assuming you run the code, you will get a blunder that drawPattern1 isn't characterized. We'll characterize it later. However, for the time being left it alone and how about we continue on to get what are Rhodonea bended curves.

Coding for Maurer Rose Curves

The above was only the hypothesis and in the event that you didn't comprehend the idea totally you will after you see it in real life. Simply add the accompanying (right above where we conjured drawPattern1):

Approach to begin with the code, Steps-by-step method:

Step 1: Drawing rose with petals n and of ‘size’ radius.

Below is the part of Source code):

def drawingRhodoneaCurve (n, size):
point = []
for i in range (0, 361):

Step 2: rhodonea curve equation

R1 = size * sin (radians (n * i))

Step 3: cartesian co-ordinates conversion

X1 = r1 * cos (radians (i))
Y1 = r1 * sin (radians (i))
list.append (point,  (width1 / 4 + x1, height1 / 4 + y1))

Step 4: set of line segments is drawn and also connected by vertices point pairs.

Step 5: setting the width1 variable to 5 and don't close path and draw it black line.

Below is the part of Source code (not meant for execution alone):

pygame.draw.lines (screen1,  (0, 0, 0), False, point, 5)
def drawPattern1 ():

Step 6: Trying to change the values to your wish.

drawingRhodoneaCurve (14, 400)

Intuitive note about the program:

The program presently isn't excessively intuitive yet you can make it intelligent by maybe expanding the quantity of petals by a fractal sum each casing and relying upon how quick/slow you increase you can get pretty great outcomes. Making the program intelligent is out of extension (since that'd' altogether increment the LOC count and maybe additionally increment the intricacy of the program and abuse the fundamental construction that we made before all else) yet I tested a little and here's the aftereffect of first making a variable n and afterward augmenting it by 0.2 at each casing!

Below is the Source code:

import pygame
from math import cos
from math import sin
from math import radians
(width1, height1) = (850, 650)
screen = pygame.display.set_mode ((width1, height1))




pygame.display.set_caption ('Rose Curve in Python \')




screen.fill ( (450, 450, 405)) # lemonChiffon colour
drawPattern1 ()
pygame.display.flip ()




while True:


for event in pygame.event.get ():




if event.type = = pygame.QUIT :




pygame.quit ()
quit ()




pygame.display.update ()




def drawingRhodoneaCurve (n, size):
point = []
for i in range (0, 361):
r1 = size * sin (radians (n * i))
x = r * cos (radians (i))
y 1= r * sin (radians (i))
list.append (points,  (width1 / 4 + x, height1 / 4 + y1))
pygame.draw.lines (screen1,  (0, 0, 0), False, point, 5)
def drawPattern1 ():
drawingRhodoneaCurve (14, 400)

Screenshot of output is presented below:

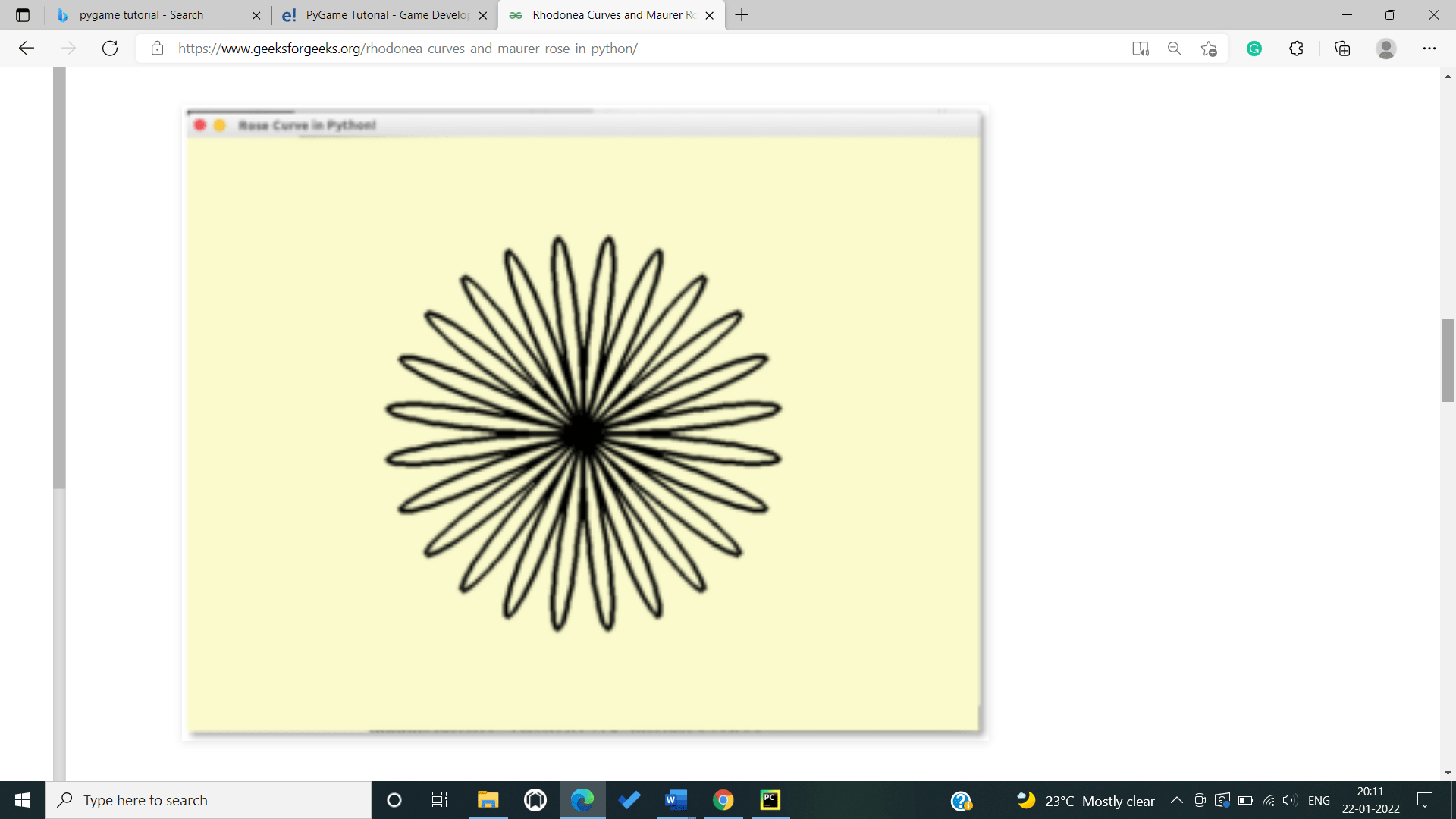
Explanation

• We ascertain the vertices (each huge point on the rose which are subsequently associated by edges which are just line-portions) utilizing the equation we examined in the above segment
• We are storing a rundown called focus which has all the vertice of the rose petals shape and later this rundown of vertice is feed to pygame.draw.lines which drawing a succession of consistents straight line and here you use it to drawing a polygonal chain like structure (since rose shape is only a polygonal chain)
• Note that we are utilizing radians technique here. This is on the grounds that the points are in degree design (we might have straightforwardly utilized radians however range anticipates just whole numbers, additionally for maurer bends we'll at any rate need to utilize degrees so why not start from now) - ideally, we didn't need to do any change ourselves as Python3 gives worked in capacities degrees and radians.
• Likewise note that we are moving the directions by (width1/4, height1/4). This is on the grounds that of course PyGame has its directions in Top-Left corner. Yet, we need it in the middle so we shift it by a large portion of the screen width1 and height1. We might have interpreted the entire direction framework however it's more straightforward along these lines!

Maurer rose

A Maurer rose of the rose r = sin (nθ) comprises of the 180 lines progressively associating the over 361 focuses. A Maurer rose is vertices on a rose and a polygonal bend. A Maurer rose comprises of certain lines that associate a few focuses on a rose bend.

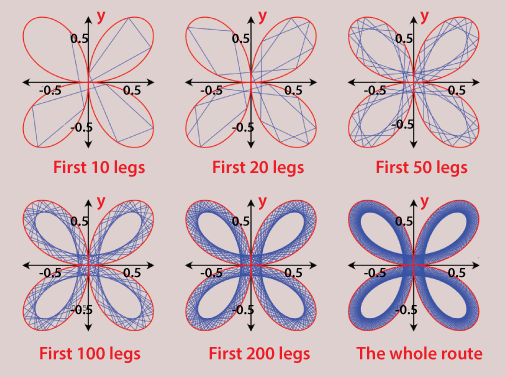
A Maurer rose is a shut bend since the beginning stage, (0, 0) and the consummation point, (sin (n·180d), 180d), correspond A Maurer rose can be portrayed as a shut course in the polar plane.). Maurer rose r = sin (nθ) is the entire cours, r is of the rose. A Maurer rose is a shut bend since the beginning stage, (0, 0) and the consummation point, (sin (n·180d), 180d), correspond.

A walker begins an excursion from the beginning, (0, 0), and strolls along a line direct (sin (nd), d). Then, at that point, in the second leg of the excursion, the walker strolls along a line to the following point, (sin (n·4d), 4d, etc. At last, in the last leg of the excursion, the walker strolls along a line, from (sin (n·359d), 359d) to the consummation point, (sin (n·180d), 180d

Coding for Maurer Roses

So, to make something out of what we recently realized, we over-compose the past drawPattern1 work with the upgraded one.

Approach to begin with the code, Steps-by-step method:

Step 1: Drawing maurer rose for d it's size and value n

Below is the part of Source code (not meant for execution alone):

def drawMaurerRose (n, d, size):
point =[]
for i in range (0, 361):

Step 2: maurer rose equation

K1 = i * d
R1 = size * sin (radians (n * k1))

Step 3: cartesian co-ordinates conversion

Below is the part of Source code (not meant for execution alone):

X1 = r1 * cos (radians (k1))
Y1 = r1 * sin (radians (k1))
list.append (point,  (width1 / 4 +x1, height1 / 4 + y1))

Step 4: Drawing a set of line segments connected by set of vertices points

Step 5: don't close the path to it and drawing it black and setting the width1 variable to 5

pygame.draw.lines (screen1,  (0, 0, 0), False, points, 5)

Step 6: Trying to change the values to your wish

def drawPattern1 ():
drawMaurerRose (6, 79, 400)

Below is the Source code:

from math import sin
from math import cos
from math import radians
import pygame
 (width1, height1) =  (850, 650)
screen = pygame.display.set_mode ( (width1, height1))




pygame.display.set_caption ('Rose Curve in Python !')




screen.fill ( (450, 450, 405)) # lemonChiffon color
drawPattern1 ()
pygame.display.flip ()




while True :


for event in pygame.event.get () :




if event.type = = pygame.QUIT :




pygame.quit ()
quit ()




pygame.display.update ()
def drawMaurerRose (n, d, size):
points =[]
for i in range (0, 361):
k1 = i * d
r1= size * sin (radians (n * k1))




x1 = r1* cos (radians (k1))
y1 = r1* sin (radians (k1))




list.append (points,  (width1 / 4 +x1, height1 / 4 + y1))




pygame.draw.lines (screen1,  (0, 0, 0), False, points, 5)




def drawPattern1 ():
drawMaurerRose (6, 79, 400)

Screenshot of output is presented below:

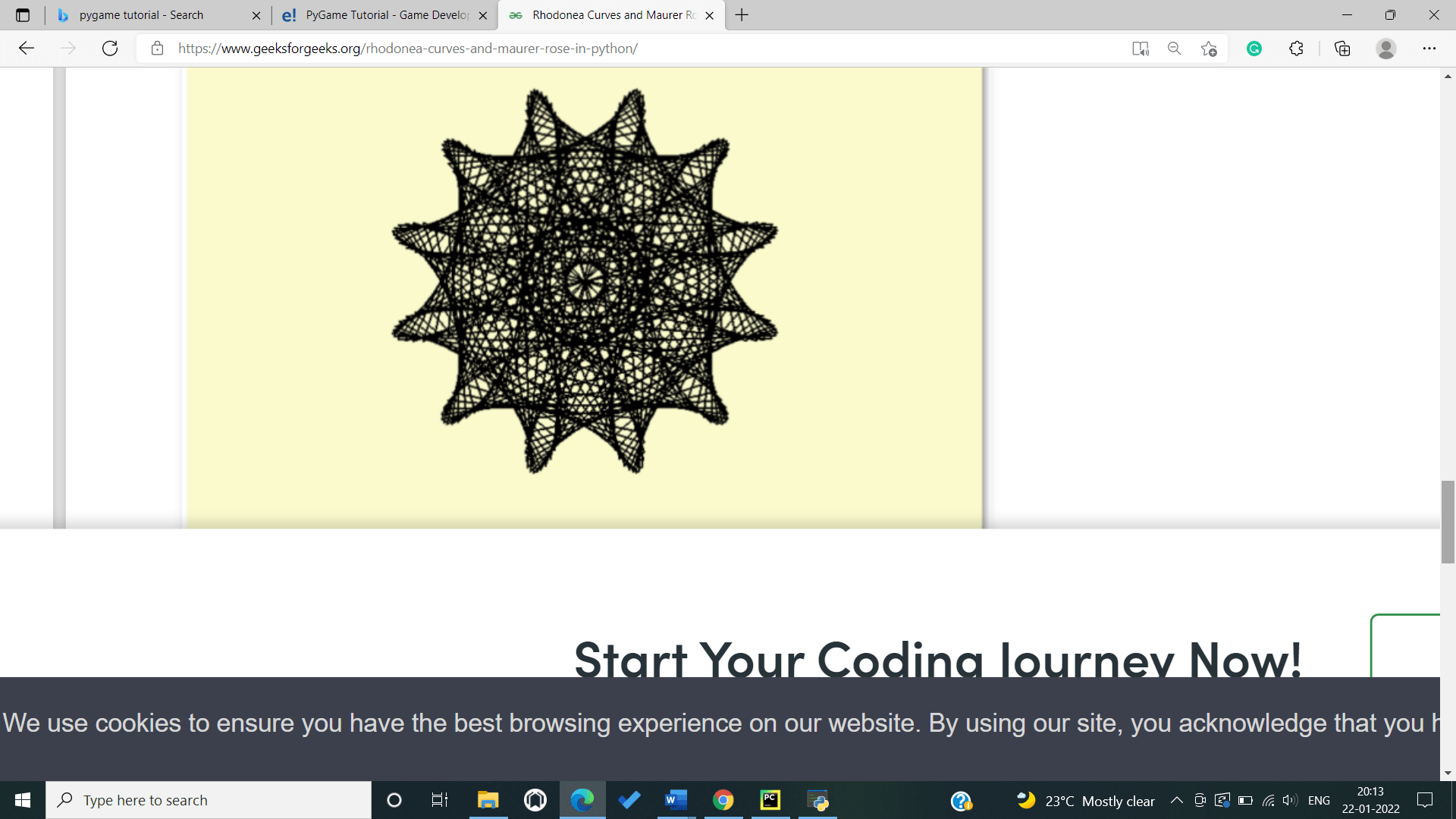
Explanation: 

• The capacity name has been changed to drawMaurerRose from drawingRhodoneaCurve and presently anticipates an additional a boundary d!
• We presently present another variable k which really comes from the equation. It's worth at every emphasis is equivalent to i*d, so for d=1 the capacity is by and large equivalent to drawingRhodoneaCurve.
• We presently utilize k rather than I and it ought to be noticed that the line width1 has been changed to 4 from 5 (if not a few lines would show up as one as a result of their high thickness).
• Furthermore the summon proclamation has ofcourse been changed too, it currently calls the recently made drawMaurerRose work with n=6 and d=71. The qualities were duplicated from WikiPedia since irregular worth of d can now and again deliver strange looking roses!