Python program to find the area of the triangle
Python program to find the area of the triangle
This article will discuss how to find the area of a triangle in Python with all three given sides. The area of a triangle represents the total region that is enclosed by the three sides of any particular triangle.
If we know the length of three sides of a triangle, then the following mathematical formula is used to calculate the area of a triangle:
Area of a Triangle = ?(s*(s-a)*(s-b)*(s-c)) Or, Area of a Triangle = sqrt of(s*(s-a)*(s-b)*(s-c))
Here a, b, c are the three sides of a triangle, and s is the semi-perimeter that can be calculated as below:
s = (a + b + c )/ 2
Source Code
The following is a source code to calculate the area of a triangle in Python:
#Program to find the area of the triangle
# Three sides of the triangle is a, b and c:
a = float(input("Enter first side: "))
b = float(input("Enter second side: "))
c = float(input("Enter third side: "))
# calculate the semi-perimeter s = (a + b + c) / 2
# calculate the area
area = (s * (s - a) * (s - b) * (s - c)) ** 0.5
print('The area of the triangle is %0.2f' % area)
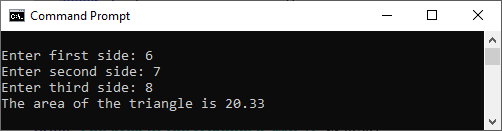
Output
Here is the output:
The following source code calculates the area of a triangle in Python by importing math function:
#import math function import math
# Three sides of the triangle
a= int(input("Enter first side: "))
b=int(input("Enter second side: "))
c=int(input("Enter third side: "))
# calculate the semi-perimeter
s=(a+b+c)/2 area=math.sqrt(s*(s-a)*(s-b)*(s-c))
#print the result print("Area of the triangle is: ",round(area,2))
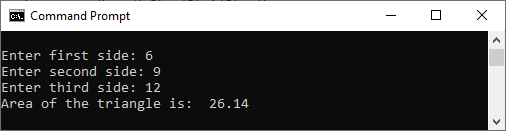
Output
Here is the output:
Explanation: In this program, a user first asks to enter the length of three sides of a triangle that will be stored in variables a, b and c, respectively. Next, it will first calculate the semi-perimeter and then calculate a triangle area using the specified mathematical expression. After performing the calculation, it will store the area in a variable area, and finally, the result will be printed on the screen.