Quick Sort in Java

Quick Sort in Java

Like merge sort, quick sort also uses the divide and conquer approach to sort the given array or list. In quick sort, the sorting of an array is achieved by taking an element from the input array as the pivot and then split the array using the pivot.

Algorithm

STEP 1: Take either the first or the last element as the pivot element.

STEP 2: Find and place the pivot element at its correct position, i.e., the elements that are on the left side of the pivot element must be less than the pivot element. Also, elements that are on the right side of the pivot element must be greater than the pivot element.

STEP 3: Recursively execute steps 1 and 2 till the whole array is sorted.

Pseudo Code

 // start --> Beginning index, end --> Last index
quickSort(arr[], start, end)
{
    if(start >= end) return; // base case
    else
    {
        // The partition() method positions the pivot
        // at the right place, i.e., left side of pivot contains
        // elements that are less than pivot and right side of
        // pivot contains elements that are greater than pivot                   
        pivot = partition(arr, start, end);
        // Invoking the method quickSort() for the left side of pivot
        quickSort(arr, start, pivot - 1); 
        // Invoking the method quickSort() for the right side of pivot
        quickSort(arr, pivot + 1, end);
    }
} 

Java Program

The following Java program implements Quick sort using the pseudo-code defined above.

FileName: QuickSortExample.java

 public class QuickSortExample
{
// The quickSort() method takes element present at the index e
// as the pivot element to do the sorting
// s is the start index
// e is the end index
static void quickSort(int arr[], int s, int e)
{
// handling base case
if(s >= e) return;
else
{
    // pivot contains the index of the pivot element
    int pivot = partition(arr, s, e);
    // recursively sorting the left side of the pivot
    quickSort(arr, s, pivot - 1);
    // recursively sorting the right side of the pivot
    quickSort(arr, pivot + 1, e);
}
}
// the partition() method finds the
// proper position of the pivot element a[e]
// by virtually splitting the array into two subarrays.
// The left subarray contains the elements that are less than the pivot element
// the right subarray contains the elements that are greater than the pivot element
static int partition(int a[], int s, int e)
{
    // low points to the last element that is
    // less than the pivot element
    int low = s - 1;
    // iterating over every element of the array,
    // except the pivot element
    for(int i = s; i < e; i++)
    {
        if(a[i] < a[e])
        {
            // ensuring that the elements of the left part
            // is less than the pivot element.
            low = low + 1;
            int temp = a[low];
            a[low] = a[i];
            a[i] = temp;
        }
    }
    // placing the pivot element
    // at the appropriate position
    int temp = a[low + 1];
    a[low + 1] = a[e];
    a[e] = temp;
    // returning the index of the pivot element.
    return low + 1;
}
// main method
public static void main(String argvs[])
{
    // given input array
    int a[] = {67, 78, 34, 12, 30, 6, 9, 21};
    // calculating size of the input array
    int size = a.length;
    System.out.println("The array before sorting is:");
    for(int j = 0; j < size; j++)
    {
        System.out.print(a[j] + " ");
    }
    System.out.println(" \n");
    // sorting the input array using quick sort
    quickSort(a, 0, a.length - 1);
    System.out.println("The array after sorting is:");
    for(int j = 0; j < size; j++)
    {
        System.out.print(a[j] + " ");
    }
}
} 

Output:

 The array before sorting is:
67 78 34 12 30 6 9 21
The array after sorting is:
6 9 12 21 30 34 67 78 

Explanation: All we have to take care is how elements less than the pivot element take the left side of the array. It is done by the for-loop present in the partition() method. When all the elements less than the pivot element take the left side of the array, the remaining elements automatically take the right side. These remaining elements are greater than the pivot element. The pivot element can then be placed just after the ending of elements that are smaller than the pivot element. Observe the following diagram.

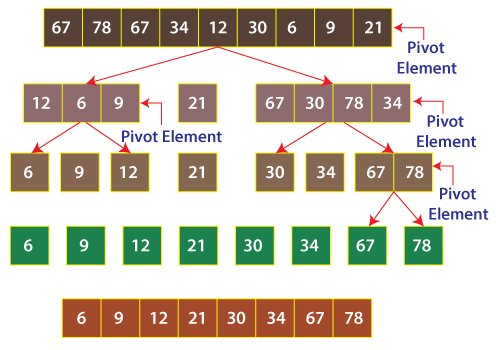
Analysis of Quick Sort

One of the main advantages of the quick sort algorithm is that it is in-place sorting. It means that it does not require no extra space for sorting. Looking from this perspective, quick sort should be preferred over the merge sort. Also, this algorithm works as quickly as merge sort.

The downsides of the algorithm are that when a sorted array is given as input, the algorithm takes O(n²) time to process the sorted array. It is worse than merge sort. It takes O(nlog(n)) time to sort the array. Note that n is the size of the input array.

Conclusion

Between merge sort and quick sort, quick sort is the better choice when the array is not sorted. If, instead of an array, a linked list is given to be sorted, go for merge sort instead of quicksort. The reason behind this is, unlike an array, randomized access of elements is not possible in a linked list, and quick sort relies heavily on the random access of elements, whereas, merge sort does not.

Also, it is found that merge sort works well for larger data sets, and quick sort works well for smaller data sets.

Time Complexity

The average and best time complexity of the quicksort is O(nlog(n)), where n is the number of elements present in the array. For sorted arrays, this sorting algorithm gives the time complexity as O(n²). Hence, the worst time complexity of this sorting algorithm is O(n²).

Space Complexity

The space complexity of the merge sort algorithm is O(1), that is, constant space complexity. Observe the code; there is no auxiliary array or any additional space used to do the sorting.