Tower of Hanoi Program in Java

Tower of Hanoi Program in Java

The Tower of Hanoi program in Java is written to solve a mathematical puzzle, called Tower of Hanoi, where we have three poles and n number of disks of different sizes. The task is to move all the n disks placed at one pole to another pole with the help of an intermediate pole. Follow the rules given below while moving the disks:

Rule 1: We can only move one disk at a time from one pole to another.

Rule 2: Only the topmost disk from any of the three given poles can be stacked to another pole.

Rule 3: The larger size disk can’t be placed on the top of a smaller disk.

The Tower of Hanoi puzzle is one of the prominent applications of recursion.

Let’s observe the Java program of the puzzle.

Filename: TowerOfHanoiExample.java

public class TowerOfHanoiExample
{
// A recursive method to find the solution of the puzzle, called Tower of Hanoi
static void twrOfHanoi(int disk, char fromPole, char toPole, char auxPole)
{
    // handling the base case
    if (disk == 1)
    {
          System.out.println("Moving disk 1 from pole " + fromPole + " to pole " + toPole);
           return;
     }
     // The first recursive call             
     // recursively moving the n - 1 disk from the source pole to the auxiliary pole
     twrOfHanoi(disk - 1, fromPole, auxPole, toPole);
      // move the nth pole from the source pole to the destination pole
      System.out.println("Moving disk " + disk + " from pole " + fromPole + " to pole " + toPole);
      // The second recursive call
      // recursively moving the n - 1 disk from the auxiliary pole to the destination pole
      twrOfHanoi(disk - 1, auxPole, toPole, fromPole);
}
       // The driver method
       public static void main(String argvs[])
       {
               int disks = 3; // total number of disks
               char firstPole = 'A'; // first pole
               char secondPole = 'B'; // second pole
               char thirdPole = 'C'; // third pole
               // invoking the method twrOfHanoi
               twrOfHanoi( disks, firstPole, thirdPole, secondPole );
      }
} 

Output:

 Moving disk 1 from pole A to pole C
Moving disk 2 from pole A to pole B
Moving disk 1 from pole C to pole B
Moving disk 3 from pole A to pole C
Moving disk 1 from pole B to pole A
Moving disk 2 from pole B to pole C
Moving disk 1 from pole A to pole C 

Explanation: In the above program, the three poles has been used to move the disks that are A, B, and C, respectively. Pole A is the source pole, where all the three disks are stacked by default. Pole C is the destination pole, and pole B is the auxiliary pole.

The task is to stack all the disks from the source pole, i.e., pole A to the destination pole, i.e., pole C, with the help of the auxiliary pole, i.e., pole B. The task is accomplished in the three following steps.

Step 1: Recursively move n – 1 disk from pole A to the pole B using pole C as the auxiliary pole.

Step 2: Move the n^th disk or the last disk, which is of the largest size, from pole A to pole C.

Step 3: Recursively move n – 1 disk from pole B to the pole C using pole A as the auxiliary pole.

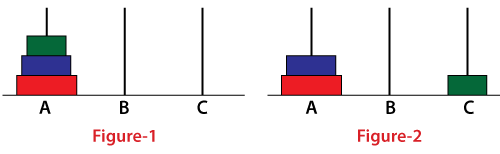
After the completion of the first step, pole A contains only one disk, the largest one. While the second and the third disk get stacked on pole B. Pole C is empty. Here, the pole C has acted as the auxiliary pole. The following diagrams illustrate the same.

Compare the disks positioning of figure-1 and figure-4. We see that pole A, B, and C contain 1, 2, and 0 disks, respectively. Figure-1 shows the initial positioning of the disks, and figure-4 demonstrates the final positioning of disks after the completion of step 1 (the first recursive call). Now, the n^th disk is moved from pole A to pole C. After that, we move the remaining disks stacked on pole B to pole C. Consider the following diagrams.

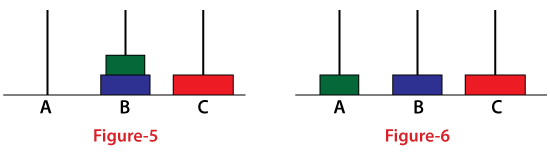
The print statement sandwiched between the recursive calls is used to move the n^th pole from the source to the destination pole (see figures 4 & 5). Now, we move to step 3 (figures 6 to 8). Here, pole A acts as the auxiliary pole and B as the source pole. All the disks eventually get stacked to the pole C.

Observe that the output contains 7 statements. Therefore, there are 7 recursive calls. The result of each recursive call is demonstrated in the above figures (figures 2 to 8). Note that, at any step we have not violated the rule to solve the puzzle.

Note: The Java program written above is a generic program and gives correct results even for a large number of disks (change the number of disks from 3 to any desired number and see yourself). For the sake of simplicity, we have chosen only 3 disks.