Heap Sort in Java

Heap sort in Java uses the data structure binary heap, min-heap, or max heap to do the sorting of elements. Since min-heap always gives the minimum element first, heap sort becomes similar to the selection sort where min-heap is used to sort the array. When max heap is used for sorting purposes, the heap sort resembles bubble sort, as max heap gives the maximum element first.

In this section, we have discussed the max-heap for sorting the elements.

Max Heap Algorithm

Step 1: Build max heap for the given input array using the method heapify().

Step 2: swap the root with the last element of the array. Reduce the size of the heap by 1.

Step 3: Call the heapify() method again to maintain the property of max heap on remaining elements.

Step 4: Repeat steps 3 & 4 till the whole array gets sorted.

Pseudo Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
 
 // Perform the operation heapify-down or down-heap for getting a max-heap
 // arr: an array representing the heap, indexing starting from 0
 // j: represents the index from where heapifying down begins
 Heapify(arr, j):
     leftChild ? 2 * j
     rightChild ? 2 * j + 1
     highest ? j
     if leftChild < size(arr) and arr[leftChild] > A[highest] then:
         highest ? leftChild
     if rightChild < size(arr) and A[rightChild] > A[highest] then:
         highest ? rightChild
     if highest ? j then:
         swap arr[j] and arr[highest]
         Heapify(arr, highest) 
 

Java Program

The following Java program implements the heap sort using the pseudo-code explained above.

FileName: HeapSortExample.java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
 
 // Java program that uses max heap to do the sorting
 public class HeapSortExample
 {
 public static void maxHeapSort(int a[])
 {
                int size = a.length;
                // rearranging array elements so that it
                // resembles max heap
                for (int j = size / 2 - 1; j >= 0; j--)
                                heapify(a, size, j);
                // One by one extract the top element, which is
                // also the maximum element from the heap
                for (int j = size - 1; j >= 0; j--)
                {
                                // Moving the maximum element of the current heap to the end
                                int tmp = a[0];
                                a[0] = a[j];
                                a[j] = tmp;
                                // invoking method heapify on the reduced heap
                                heapify(a, j, 0);
                }
 }
 // The heapfiy() method does the rearrangement of elements of
 // the given input array to resemble it like a max heap
 // Element present at the index j resembles the root of the max heap
 // length gives the size of the max heap
 static void  heapify(int a[], int length, int j)
 {
                int highest = j; // assign highest as root
                int left = 2 * j + 1; // leftChild = 2 * j + 1
                int right = 2 * j + 2; // rightChild = 2 * j + 2
                // If the root element is smaller the left child
                if (left < length && a[left] > a[highest])
                                highest = left;
                // If the root element so fat is smaller the right child
                if (right < length && a[right] > a[highest])
                                highest = right;
                // If root is not the highest
                if (highest != j)
                {
                                int change = a[j];
                                a[j] = a[highest];
                                a[highest] = change;
                                // Heapifying the affected sub-tree recursively
                                heapify(a, length, highest);
                }
 }
 // main method
 public static void main(String argvs[])
 {
     // given input array
     int a[] = {67, 78, 34, 12, 30, 6, 9, 21};
     // calculating size of the array
     int size = a.length;
     System.out.println("The array before sorting is: ");
     for(int i = 0; i < size; i++)
     {
        System.out.print(a[i] + " ");
     }
     System.out.println("\n");
     // invoking method maxHeapSort()
     maxHeapSort(a);
     System.out.println("The array after sorting is: ");
     // displaying the sorted array
     for(int i = 0; i < size; i++)
     {
         System.out.print(a[i] + " ");
     }
 }
 } 
 

Output:

1
2
3
4
5
6
 
 The array before sorting is:
 67 78 34 12 30 6 9 21
 The array after sorting is:
 6 9 12 21 30 34 67 78 
 

Explanation: The above program is imitating bubble sort. The heapify() method ensures that the maximum value element sits at the index 0. Then in one swap, the maximum element is put at the end of the array. When the heapify() method is called the second time, it puts the second maximum element at index 0.

The swapping process puts the second maximum element at the second last index of the array, and the process of invoking the heapify() method and swapping of elements continues till the whole array is sorted. The following diagram demonstrates the same.

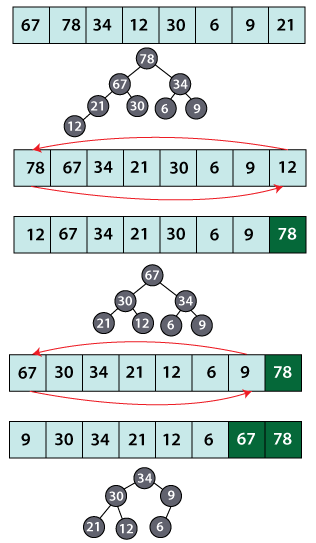
Note that instead of using the max-heap, min-heap can also be used to sort. Using the min-heap, the heap sort resembles the selection sort as the root of the min-heap always gives the element of least value.

Analysis of the Heap Sort

Even though heap sort resembles the selection or bubble sort, the heap sort is much faster than the selection or bubble sort. However, similar to the selection or bubble sort, heap sort also divides the input array virtually into two halves; one is sorted, and another is unsorted.

Time Complexity

The heapify() method does the heapification process in O(log(n)) times, where n is the size of the input array. Also, the for-loop is iterating over each element of the array from right to left (see code). In each iteration, the heapify() method is invoked. Thus, for the for-loop time complexity is O(n) and O(log(n)) for the heapify() method. Hence, the total time complexity turns out to be O(n * log(n)) = O(nlog(n)). As O(nlog(n) is always less than O(n^2); therefore, heap sort is better than selection or bubble sort. One can think of the heap sorting algorithm as an improved version of selection sort or bubble sort.

Space Complexity

Similar to selection or bubble sort, heap sort algorithm also does the in-place sorting. The heap sort tries to visualize the input array as either min heap or max heap. Therefore, the space complexity for the heap sort turns out to be O(1), i.e., constant space for sorting the input array or list.

Conclusion

Heap sort works faster than bubble or selection sort. However, for larger data sets, it is found that merge sort is a better choice than heap sort, even though merge as well heap sort gives the time complexity of O(nlog(n)). Also, unlike merge sort, heap sort is not a stable sorting algorithm. However, by some modification, one can make merge sort stable. However, making heap sort stable increases the complexity of the algorithm.

Java Tutorial Index

Java Loops

Java Programs

Java Sorting

Java OOPs Concepts

Java Strings

Java Exceptions

Garbage Collection

Multithreading

Java IO

Serialization

Networking

AWT

Swing

Java Collections

Java Generics

Java Annotations

Java JDBC

Java Differences

How to

Java 8 Features

Java 9 Features

Java 12

Java 13

Java 14

Java 15

Java 16

Java 17

Java Math Methods

Java String Methods

Java Conversion

Java Keywords

Java Problems

Java Questions

Java Interview Questions

Misc

Heap Sort in Java

Heap Sort in Java